Adjusting a Momentum-Based Golf Clubhead-Ball Impact Model to Improve Accuracy †
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Data
2.2. Momentum-Based Clubhead-Ball Impact Model
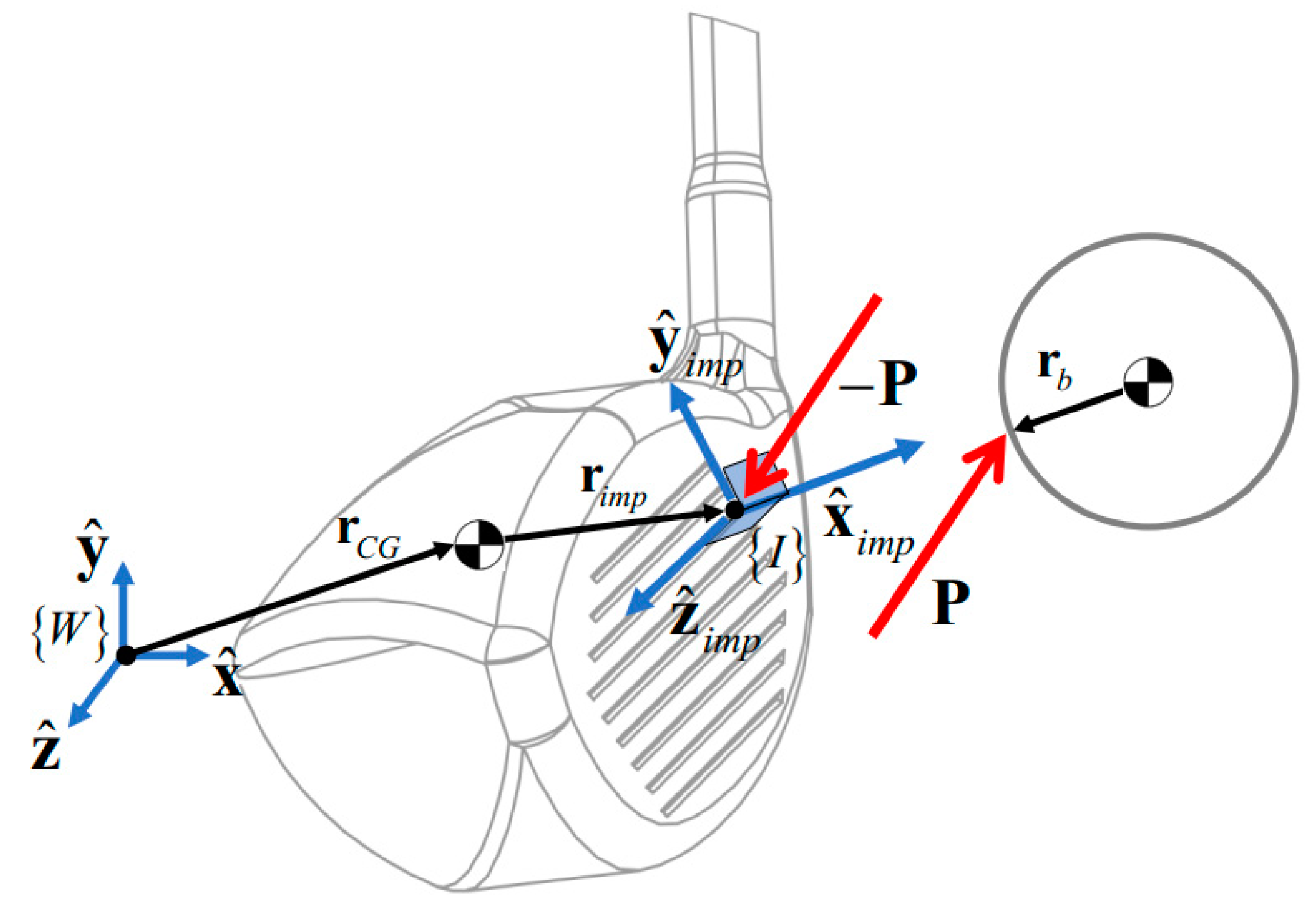
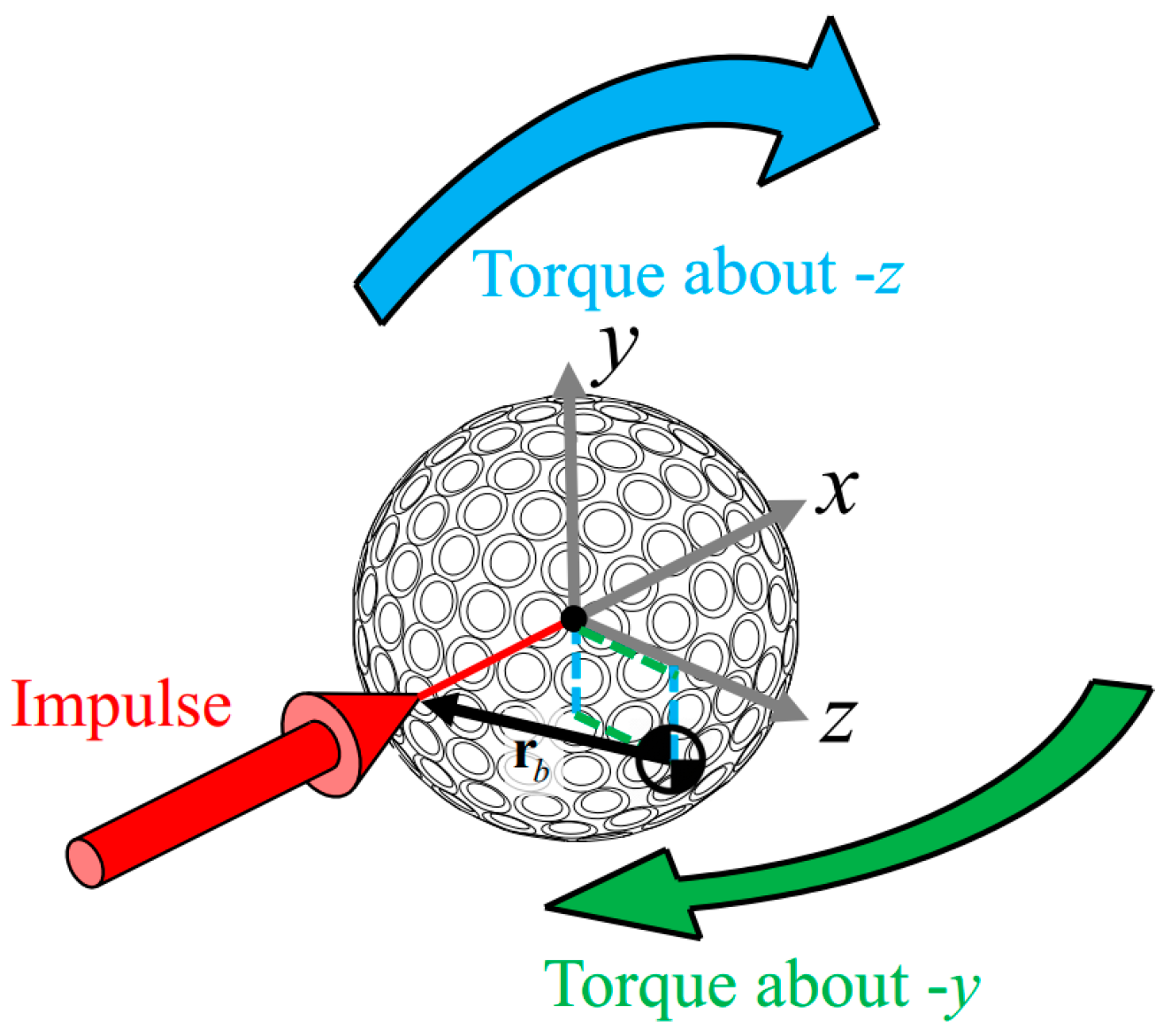
2.2.1. Equations of Impulse and Momentum
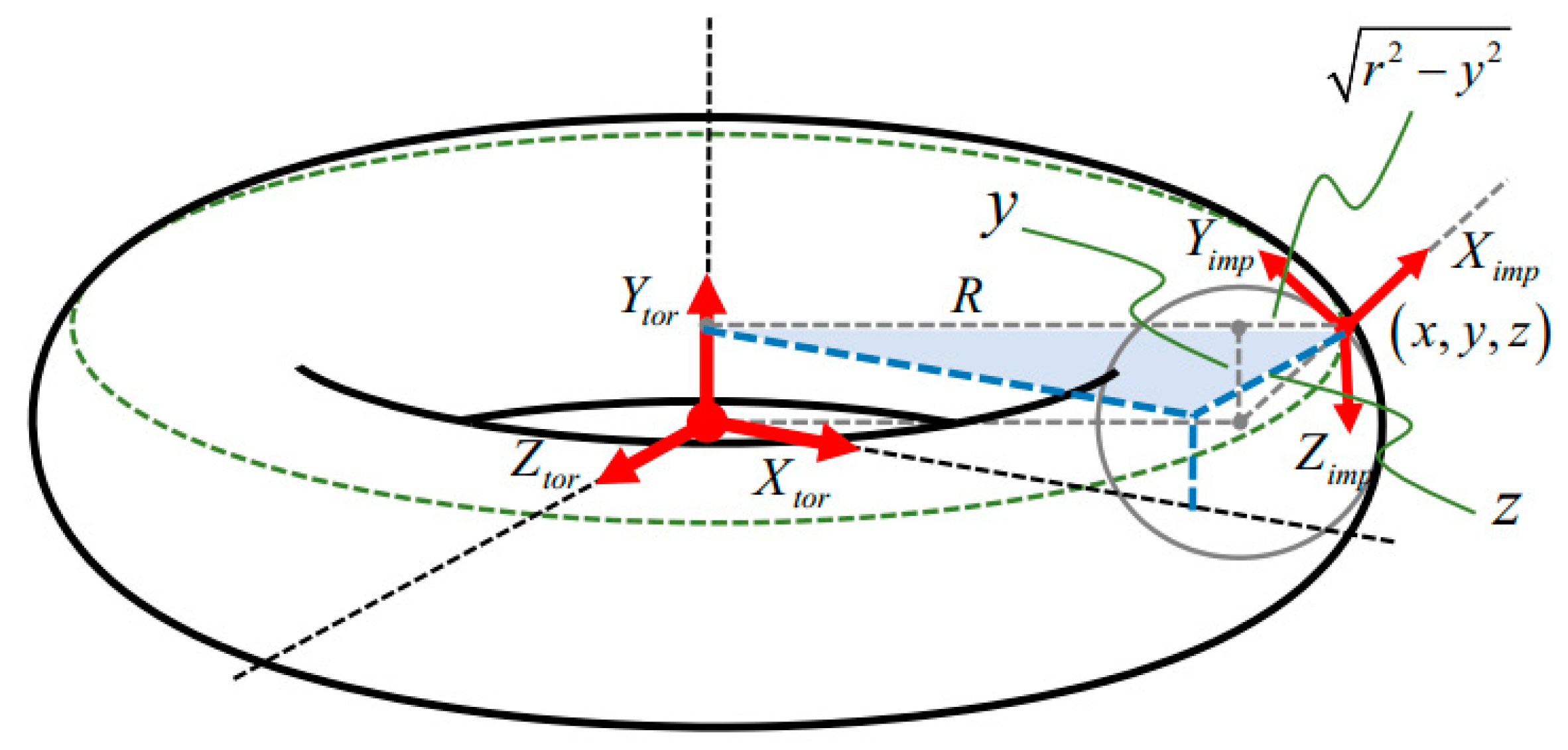
2.2.2. Clubhead Face Geometry
2.2.3. Prediction Errors for Nominal Parameters
2.3. Impact Model Augmentation
3. Results and Discussion
4. Conclusions
Conflicts of Interest
References
- Petersen, W.; McPhee, J. Comparison of impulse-momentum and finite element models for impact between golf ball and clubhead. In Science and Golf V: Proceedings of the World Scientific Congress of Golf, Phoenix; Energy in Motion, Inc.: Mesa, AZ, USA, 2008. [Google Scholar]
- McNally, W.; Balzerson, D.; Wilson, D.; McPhee, J. Effect of Clubhead Inertial Properties and Driver Face Geometry on Golf ball Trajectories. Procedia Eng. 2016, 147, 407–412. [Google Scholar] [CrossRef][Green Version]
- Winfield, D.; Tan, T. Optimization of clubhead loft and swing elevation angles for maximum distance of a golf drive. Comput. Struct. 1994, 53, 19–25. [Google Scholar] [CrossRef]
- Tanaka, K.; Teranishi, Y.; Ujihashi, S. Finite element modelling and simulations for golf impact. Proc. Inst. Mech. Eng. Part P: J. Sports Eng. Technol. 2012, 227, 20–30. [Google Scholar] [CrossRef]
- McNally, W.; McPhee, J.; Henrikson, E. The golf shaft’s influence on clubhead-ball impact dynamics. Proceedings 2018, 2, 245. [Google Scholar]
- McNally, W.; Henrikson, E.; McPhee, J. A continuous analytical shaft model for fast dynamic simulation of the golf swing. Sports Eng. 2019, 22, 20. [Google Scholar] [CrossRef]

| Parameter | Value | Description |
|---|---|---|
| 204 | Mass of the clubhead (g). | |
| Position of the center of mass (C) of the clubhead with reference to Center of Face (CoF) expressed in CoF reference frame (mm). | ||
| (g·cm2). | ||
| 45.9 | Mass of the golf ball (g). | |
| Inertia matrix of the golf ball (g·cm2). | ||
| coordinate frame (mm). | ||
| 0.83 | Coefficient of restitution. | |
| Loft | Loft angle. | |
| Bulge | 305 | Bulge (mm). |
| Roll | 305 | Roll (mm). |
| Velocity Type | Component | Shaft A | Shaft B | Shaft C | |||
|---|---|---|---|---|---|---|---|
| Mean | STD | Mean | STD | Mean | STD | ||
| Linear velocity | Speed (mph) | −0.73 | 1.41 | −0.49 | 1.35 | −0.58 | 1.31 |
| Launch angle (deg) | −1.18 | 0.88 | −0.94 | 1.03 | −0.85 | 0.85 | |
| Azimuth angle (deg) | −0.86 | 0.48 | −0.94 | 0.54 | −0.89 | 0.53 | |
| Angular velocity | Back-spin (rpm) | 741 | 450 | 741 | 479 | 790 | 401 |
| Side-Spin (rpm) | 187 | 178 | 187 | 210 | 187 | 166 | |
| Velocity Type | Component | Shaft A | Shaft B | Shaft C | |||
|---|---|---|---|---|---|---|---|
| Mean | STD | Mean | STD | Mean | STD | ||
| Linear velocity | Speed (mph) | 0.027 | 1.35 | 0.018 | 1.29 | 0.02 | 1.25 |
| Launch angle (deg) | −1.98 | 0.89 | −1.73 | 1.03 | −1.72 | 0.85 | |
| Azimuth angle (deg) | −1.07 | 0.49 | −1.15 | 0.55 | −1.1 | 0.53 | |
| Angular velocity | Bactablek-spin (rpm) | 111 | 452 | 110 | 476 | 95 | 399 |
| Side-Spin (rpm) | 34 | 173 | 30 | 209 | 24 | 163 | |
| Parameter | Shaft A | Shaft B | Shaft C |
|---|---|---|---|
| 2.54 | 0.88 | 1.18 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Danaei, B.; McNally, W.; Henrikson, E.; McPhee, J. Adjusting a Momentum-Based Golf Clubhead-Ball Impact Model to Improve Accuracy. Proceedings 2020, 49, 47. https://doi.org/10.3390/proceedings2020049047
Danaei B, McNally W, Henrikson E, McPhee J. Adjusting a Momentum-Based Golf Clubhead-Ball Impact Model to Improve Accuracy. Proceedings. 2020; 49(1):47. https://doi.org/10.3390/proceedings2020049047
Chicago/Turabian StyleDanaei, Behzad, William McNally, Erik Henrikson, and John McPhee. 2020. "Adjusting a Momentum-Based Golf Clubhead-Ball Impact Model to Improve Accuracy" Proceedings 49, no. 1: 47. https://doi.org/10.3390/proceedings2020049047
APA StyleDanaei, B., McNally, W., Henrikson, E., & McPhee, J. (2020). Adjusting a Momentum-Based Golf Clubhead-Ball Impact Model to Improve Accuracy. Proceedings, 49(1), 47. https://doi.org/10.3390/proceedings2020049047





