Optimal Shooting Cadence in the Laser-Run Trial of Modern Pentathlon ^†

Abstract

In the laser-run trial in modern pentathlon, athletes must perform series of five successful shots with a laser pistol. A miss does not lead to a penalty but costs the time needed to lower the arm, charge the weapon and raise the arm. Pentathletes face the following dilemma: is it better to shoot fast or accurately? We investigate experimentally the effect of the shooting cadence on the accuracy. We then predict the consequence of this unavoidable speed-accuracy tradeoff in terms of total time needed to succeed the specific trial of laser-run. We find an optimal shooting cadence for each athlete, which minimizes this time.

1. Introduction

The maximum accuracy of controlled movements of humans as well as machines is generally obtained when they are executed slower than the maximum available speed. This reveals an unavoidable trade-off when confronted with the task of executing a move both fast and accurate [1,2,3]. Since the founding work of Woodworth in 1899 [4], a rich literature has been produced to explain the origin of the speed-accuracy trade-off in human movements, for which numerous models have been proposed [5,6,7,8]. One of the most important findings was perhaps the discovery by Fitts of a logarithmic relationship between the typical time needed to succeed in an aiming task and its “index of difficulty”, related to the ratio of the typical size of the aimed target to the typical distance covered in the movement [9]. This relationship, known as Fitts’s law, or some slightly modified variants, has been shown to hold in a wide variety of tasks [10].

The laser-run trial in modern pentathlon is a model situation of such a trade-off in sport. In this decisive combined event [11], the athletes must run four laps of 800 m on a cross track and the winner is the athlete crossing the finish line first. Before each lap, they must stop at the shooting range, where their laser pistol awaits them. They shoot at an electronic target placed at a distance of 10 m, and must hit it 5 times to be allowed to resume running. A miss induces no penalty but the athlete must shoot again and lower the pistol on the table between two shots, which implies that missing the target costs time. Pentathletes thus face the following dilemma: shooting slowly may help improve their accuracy and avoid time costly misses, but it also increases the time taken for each shot and thus the total time to hit the target five times. On the contrary, shooting fast reduces the time of each shot but the haste may provoke misses. Pentathletes need to find the optimal trade-off between speed and accuracy to minimize the total time spent at the shooting range. Biomechanical analyses of the shooting movement have been performed [12,13], such as the effect of the running phase on the shooting performance [14,15]. Nonetheless, no studies have been conducted on the effect of the shooting cadence. In this article, we first investigate experimentally its influence on performance in the laser-run trial. We then discuss the existence of an optimal choice for the shooting cadence.

2. Materials and Methods

To investigate the speed accuracy trade-off in laser shooting, we perform the following experiment. We ask an elite pentathlete from French team to shoot at fixed cadences using a metronome, and we measure his accuracy. The shooter is located 10 m away from a 59.5 mm diameter electronic target used for training and competitions, and uses his own laser pistol [IQ power shooting]. An example of one shooting sequence is shown on Figure 1a. We note $\theta$ the angle of the shooting arm with time. The time evolution of this angle is plotted on Figure 1b for a series of five consecutive shots. The shot time $\Delta t$ is here imposed at 2.0 s. Each shot is divided into three phases: first, the shooter quickly raises his arm until a few centimeters under the target. Then, he slows down and aims at the target. Finally, he shoots and lowers his arm to recharge the pistol. Those three phases are materialized in, respectively, red, blue and green.

We vary the metronome’s cadence from 50 to 14 beats per minute, which corresponds to 1.2 to 4.3 s between each shoot. For each cadence, the shooter performs two or three training series of a dozen shots each, to accustom himself with the cadence. He then performs between 100 and 200 shots by series of a dozen shots, with a pause of several minutes between each. It has been shown that running poorly affects shooting performance [15]. The experiments are therefore done at rest (without running) and are spread out over several weeks to minimize the effects of tiredness, or daily environmental conditions. We use a camera recording an image of the target at 60 fps to measure the exact time and location of the shots on the target. We also perform the same experiment in similar conditions with a novice shooter, to compare the results. Nonetheless, the novice was standing 4 m from the target, in order to reach a reasonable accuracy.

3. Results

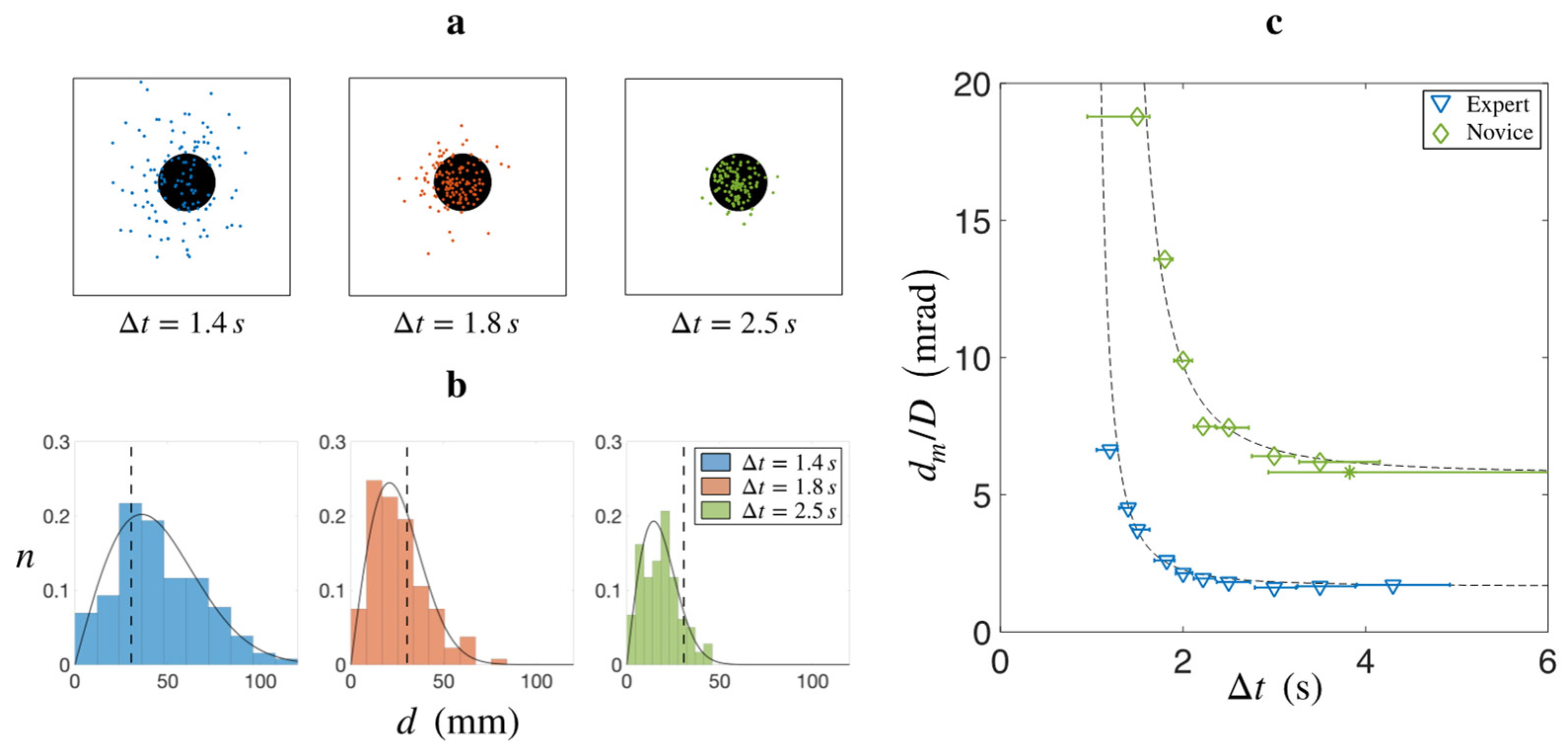
3.1. Evolution of Accuracy with Shooting Cadence

We present, on Figure 2a, the shot distribution of the elite pentathlete measured at three characteristic cadences (1.4, 1.8 and 2.5 s respectively). For each cadence, the black disk represents the target of diameter 59.5 mm and the points show the impact locations of the shots. Figure 2b presents the corresponding distributions of distances from the center of the target. As the time available for aiming increases, we observe that both the mean value and the spread of the distances from the center decrease. The measured distributions can be approximated by radial Gaussian curves (black solid lines) of which the equation is:

$$n\left(d\right)=\frac{\pi d}{2d_m^2}{e}^{-\frac{\pi d^2}{4d_m^2}}\delta d,$$

(1)

where $d_m$ is the mean value of the distance from the center of the target, and $n\left(d\right)$ is the proportion of shots lying between $d$ and $d+\delta d$. The evolution of $d_m/D$ (where $D$ is the distance between the shooter and the target) with the shooting cadence is shown in Figure 2c. It is plotted for the elite pentathlete (blue triangles) and for the novice shooter (green diamonds). The green star for the novice was obtained by asking him to take as much time as needed to be as accurate as possible. The mean distance strongly decreases with increasing small shooting times and then saturates at large shooting times. It reaches a value close to $1.6$ mrad for the expert, and $6$ mrad for the novice. By comparison, the angular radius of the target is $2.98$ mrad at $10$ m. It is remarkable that the behavior is very similar for the expert and the novice, and is consistent with standard models of the speed-accuracy trade-off. The black dashed lines show the best fit using the model from [16], of which the equation is:

$$d_m\left(\Delta t\right)=d_{lim}\left(1+{\left(\frac{t_c}{\Delta t-t_{lim}}\right)}^2\right).$$

(2)

$d_{lim}$ is the limit for infinite shooting time $\Delta t$ and can be interpreted as the minimum characteristic distribution size performed by the shooter without time constraint. $t_{lim}$ can be interpreted as the minimum time required for the shooter to perform the shooting gesture (raising its arm) and $t_c$ is a characteristic time quantifying the time needed by the shooter to reach $d_{lim}$. The parameters $d_{lim}$ and $t_{lim}$ were estimated independently by respectively asking the shooter to shoot as accurate as possible without time constraint and to perform the shooting gesture as fast as possible (no aiming). We found, for the elite shooter $d_{lim}/D=1.6$ mrad, $t_{lim}=0.9$ s and $t_c=0.67$ s, and for the novice $d_{lim}/D=5.8$ mrad, $t_{lim}=1.0$ s and $t_c=0.75$ s.

The increase in accuracy with the time between two shots is reported in terms of proportion $P$ of successful shots (inside the target) in Figure 3a. The blue triangles (respectively the green diamonds) represent the measured percentage of successful shots for the elite pentathlete at 10 m (respectively for the novice shooter at 4 m). It is noteworthy that the curves of the novice and of the experimented shooter have similar shapes: we observe in both cases that the accuracy P remains at a high constant level ($\approx 95\%$ for the expert and $\approx 75\%$ for the novice) above a critical shooting time (of the order of a few seconds), below which it decreases sharply. Since increasing shooting speed decreases the percentage of successful shots, this curve characterizes the speed-accuracy trade-off in the shooting task. Below 1.2 s for the elite pentathlete (1.6 s for the novice shooter, respectively), the shooter could not shoot at the specified pace anymore. The black dashed line is the model obtained from [16]:

$$P\left(\Delta t\right)=1-e^{-\frac{\pi r_t^2}{4{(d_m\left(\Delta t\right))}^2}},$$

(3)

where $r_t$ is the radius of the target and $d_m\left(\Delta t\right)$ is given by Equation (2). It is again consistent with the experimental data.

3.2. Total Shooting Time

In the laser run trial of pentathlon, the essential quantity is the time needed to achieve five successful shots (not necessarily consecutive). We thus measure, for each cadence, the average value of this time, and report the results on Figure 3b (blue triangles for the elite pentathlete and green diamonds for the novice shooter). Note that, in modern pentathlon competitions, the timer starts counting the time at the moment of the first shot. Because we want to measure this quantity the same way the athletes do, we choose to adopt their convention and record the time separating the first successful shot from the fifth one. We also plot, on a dashed black line, the theoretical expression of the total time from [16], of which the expression is:

$$T=\frac{5\Delta t}{P\left(\Delta t\right)}-\Delta t,$$

(4)

where $P\left(\Delta t\right)$ is given by Equation (3).

The curves of the elite shooter and of the novice have similar shapes again. They reveal the existence of an optimal shooting cadence (2.1 s for the elite and 2.7 s for the novice), corresponding to the best balance between speed and accuracy in this sport. The optimal cadence is far below the fastest that the shooter can reach and it corresponds to a shooting accuracy far below the maximal one he can achieve. The laser-run trial of pentathlon is in this sense a paradigm of speed accuracy trade-off situation, where the best strategy naturally lies in-between being as fast as possible or being as accurate as possible. The first place in laser-run is often played at a few seconds. Therefore, shooting at the optimal cadence can be decisive for the athlete. What is more, the asymmetry of the curve on Figure 3b reveals the danger for the pentathlete to shoot faster than his optimal cadence. Indeed, the total time $T$ increases drastically if the shooting time $\Delta t$ decreases a bit from the optimal value. On the contrary, it slowly increases if $\Delta t$ increases. A pentathlete should then shoot a bit slower than his optimal shooting time, in order to avoid the left part of the curve.

4. Conclusions

In this paper, we investigated the consequences of the speed accuracy trade-off on an aiming and shooting task, in the context of the laser-run trial in modern pentathlon. Experiments on elite and novice shooters were performed to measure the accuracy at different shooting cadences. The results in both cases are consistent with the same speed accuracy trade-off motion model [16]. We showed the effects of this loss of accuracy on performance of pentathletes in the trial and revealed an optimal cadence for each athlete, which minimizes the total time spent at the shooting range. The asymmetry of the relationship between the total time and shooting cadence also reveals the risk of shooting too fast. The measure of the speed accuracy trade-off relation for each person may be used as a training tool for coaches to evaluate and improve the performance of the athletes. The laser-run trial is a powerful archetype of the consequences of the speed accuracy trade-off on movement efficiency and kinetics, but these results may be generalized to any problem where the goal is to find the minimum mean time to succeed in a binary task (won or lost).