Blockage Correction and Reynolds Number Dependency of an Alpine Skier: A Comparison Between Two Closed-Section Wind Tunnels †
Abstract
:1. Introduction
1.1. Blockage Effect
1.2. Reynolds Number Dependency
2. Methods
2.1. Wind Tunnel Testing
2.2. Frontal Area Measurements

2.3. Blockage Effect Correction
2.4. Reynolds Number Dependency
3. Results and Discussion
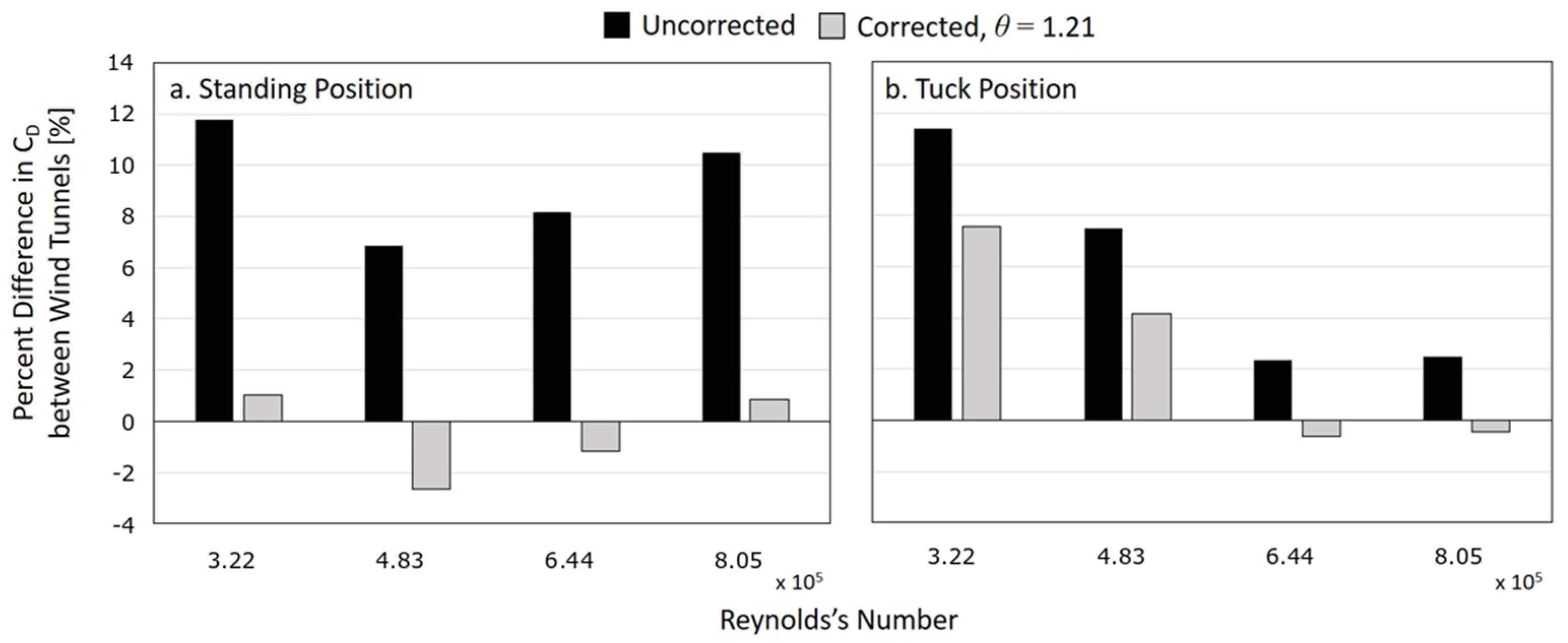
3.1. Blockage Effect Correction
3.2. Reynolds Number Dependency
4. Conclusions
Acknowledgments
References
- Savolainen, S.; Visuri, R. A review of athletic energy expenditure, using skiing as a practical example. J. Appl. Biomech. 1994, 10, 253–269. [Google Scholar] [CrossRef]
- Watanabe, K.; Ohtsuki, T. Postural changes and aerodynamic forces in alpine skiing. Ergonomics 1977, 20, 121–131. [Google Scholar] [CrossRef]
- Meyer, F.; Le Pelley, D.; Borrani, F. Aerodynamic drag modeling of alpine skiers performing giant slalom turns. Med. Sci. Sports Exerc. 2012, 44, 1109–1115. [Google Scholar] [CrossRef]
- Supej, M.; Sætran, L.; Oggiano, L.; Ettema, G.; Šarabon, N.; Nemec, B.; Holmberg, H.C. Aerodynamic drag is not the major determinant of performance during giant slalom skiing at the elite level. Scand. J. Med. Sci. Sports 2013, 23, 38–47. [Google Scholar] [CrossRef]
- Elfmark, O.; Bardal, L.M. An Empirical Model of Aerodynamic Drag in Alpine Skiing. Proceedings 2018, 2, 310. [Google Scholar]
- Battisti, L.; Zanne, L.; Anna, S.D.; Dossena, V.; Persico, G.; Paradiso, B. Aerodynamic measurements on a vertical Axis wind turbine in a large scale wind tunnel. J. Energy Resour. Technol. 2011, 133, 1–9. [Google Scholar] [CrossRef]
- Molina, A.C.; De Troyer, T.; Massai, T.; Vergaerde, A.; Runacres, M.C.; Bartoli, G. Effect of turbulence on the performance of VAWTs: An experimental study in two different wind tunnels. J. Wind Eng. Ind. Aerodyn. 2019, 193, 103969. [Google Scholar] [CrossRef]
- Anthoine, J.; Olivari, D.; Portugaels, D. Wind-tunnel blockage effect on drag coefficient of circular cylinders. Wind Struct. 2009, 12, 541–551. [Google Scholar] [CrossRef]
- Maskell, E.C. A Theory of the Blockage Effects on Bluff Bodies and Stalled Wings in a Closed Wind Tunnel; No. ARC-R/M-3400; Aeronautical Research Council: London, UK, 1963.
- Oggiano, L.; Sætran, L.; Løset, S.; Winther, R. Reducing the athlete’s aerodynamical resistance. J. Comput. Appl. Mech. 2007, 8, 163–173. [Google Scholar]


| Wind Tunnel | Test Section [m] (Width × Height) | Blockage Ratio [%] (Standing/Tuck) | Max Wind Speed [m/s] | Force Balance | Ti [%] |
|---|---|---|---|---|---|
| NTNU | 2.7 × 1.8 (4.9) | 11.7/5.6 | 25 | Schenck 6-comp. | <0.24 |
| PoliMi | 4 × 3.84 (15.4) | 3.5/1.7 | 55 | RUAG Aerospace 6-comp. | <0.1 |
| Blockage Constant | Standing | Tuck | Combined |
|---|---|---|---|
| None (no correction) | 8.9 | 4.0 | 7.7 |
| θ = 2.58 | 9.4 | 1.8 | 6.6 |
| θ = 0.96 | 1.8 | 2.2 | 2.4 |
| θ1 = 1.15, θ2 = 2.52, θ3 = 1.21 | 1.5 | 1.8 | 2.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elfmark, O.; Reid, R.; Bardal, L.M. Blockage Correction and Reynolds Number Dependency of an Alpine Skier: A Comparison Between Two Closed-Section Wind Tunnels. Proceedings 2020, 49, 19. https://doi.org/10.3390/proceedings2020049019
Elfmark O, Reid R, Bardal LM. Blockage Correction and Reynolds Number Dependency of an Alpine Skier: A Comparison Between Two Closed-Section Wind Tunnels. Proceedings. 2020; 49(1):19. https://doi.org/10.3390/proceedings2020049019
Chicago/Turabian StyleElfmark, Ola, Robert Reid, and Lars Morten Bardal. 2020. "Blockage Correction and Reynolds Number Dependency of an Alpine Skier: A Comparison Between Two Closed-Section Wind Tunnels" Proceedings 49, no. 1: 19. https://doi.org/10.3390/proceedings2020049019
APA StyleElfmark, O., Reid, R., & Bardal, L. M. (2020). Blockage Correction and Reynolds Number Dependency of an Alpine Skier: A Comparison Between Two Closed-Section Wind Tunnels. Proceedings, 49(1), 19. https://doi.org/10.3390/proceedings2020049019




