Investigation of Influence of Adjustments in Cyclist Arm Position on Aerodynamic Drag Using Computational Fluid Dynamics †
Abstract
:1. Introduction
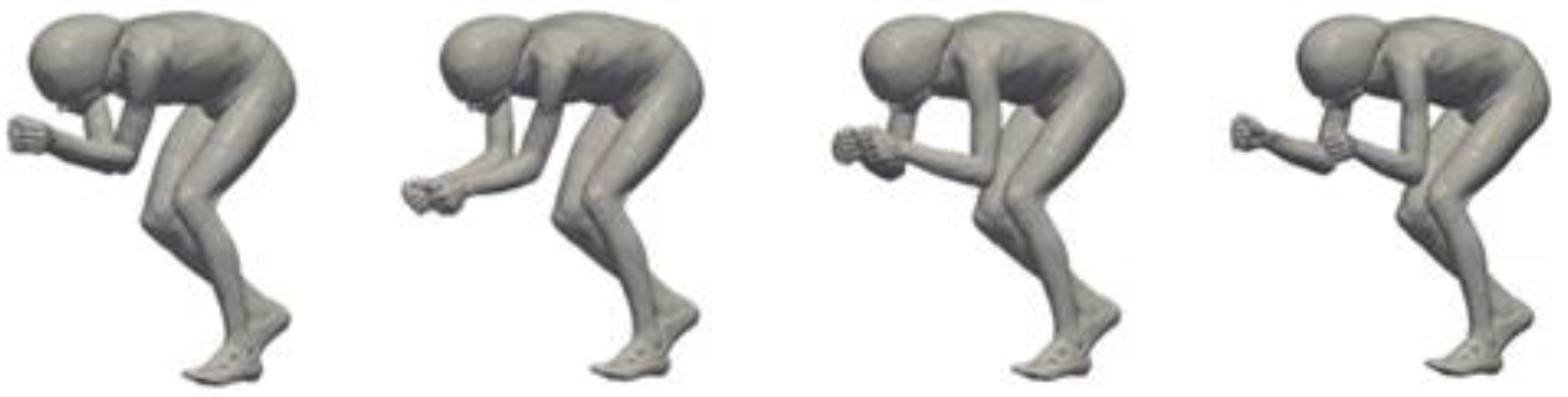
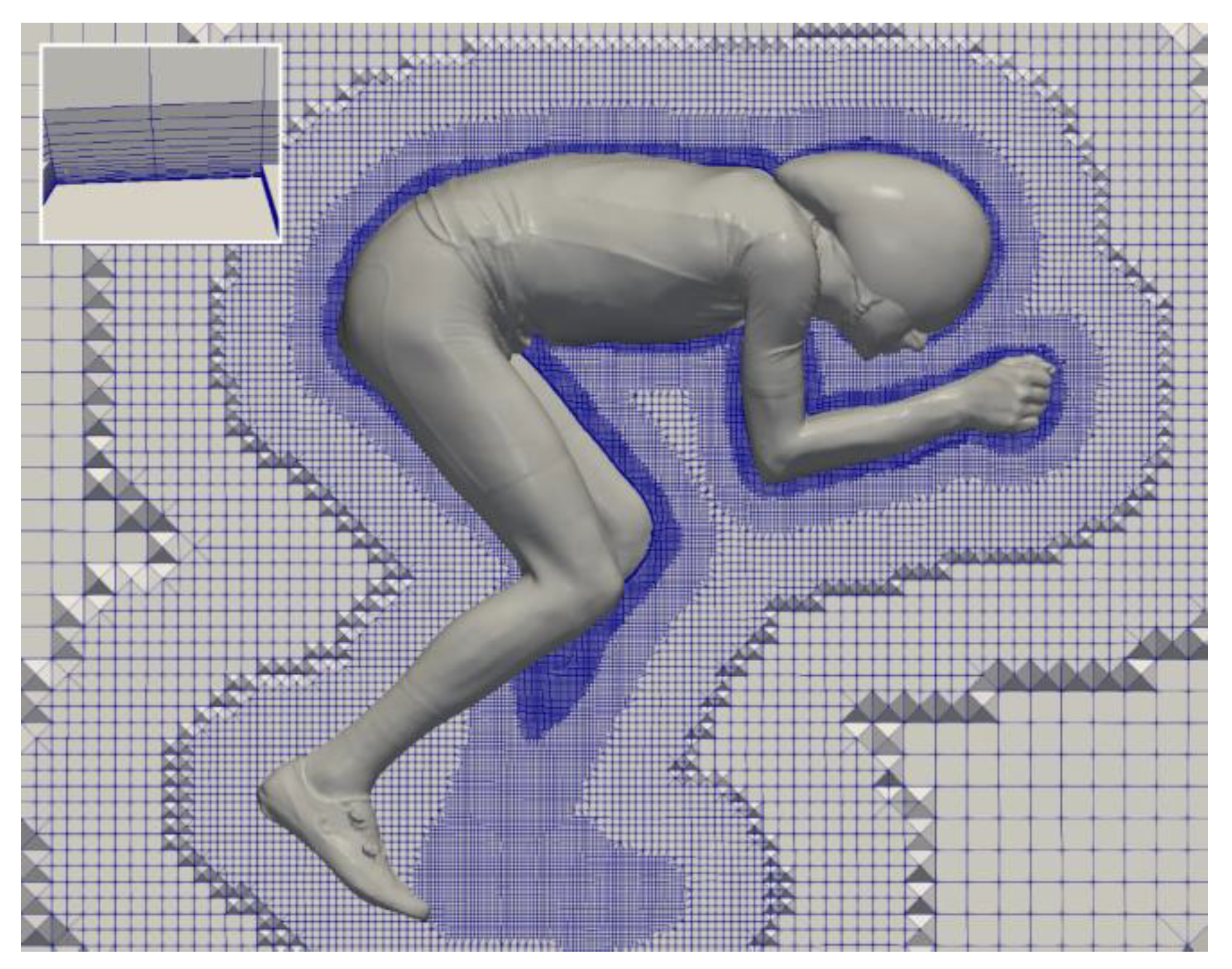
2. Materials and Methods
3. Results and Discussion
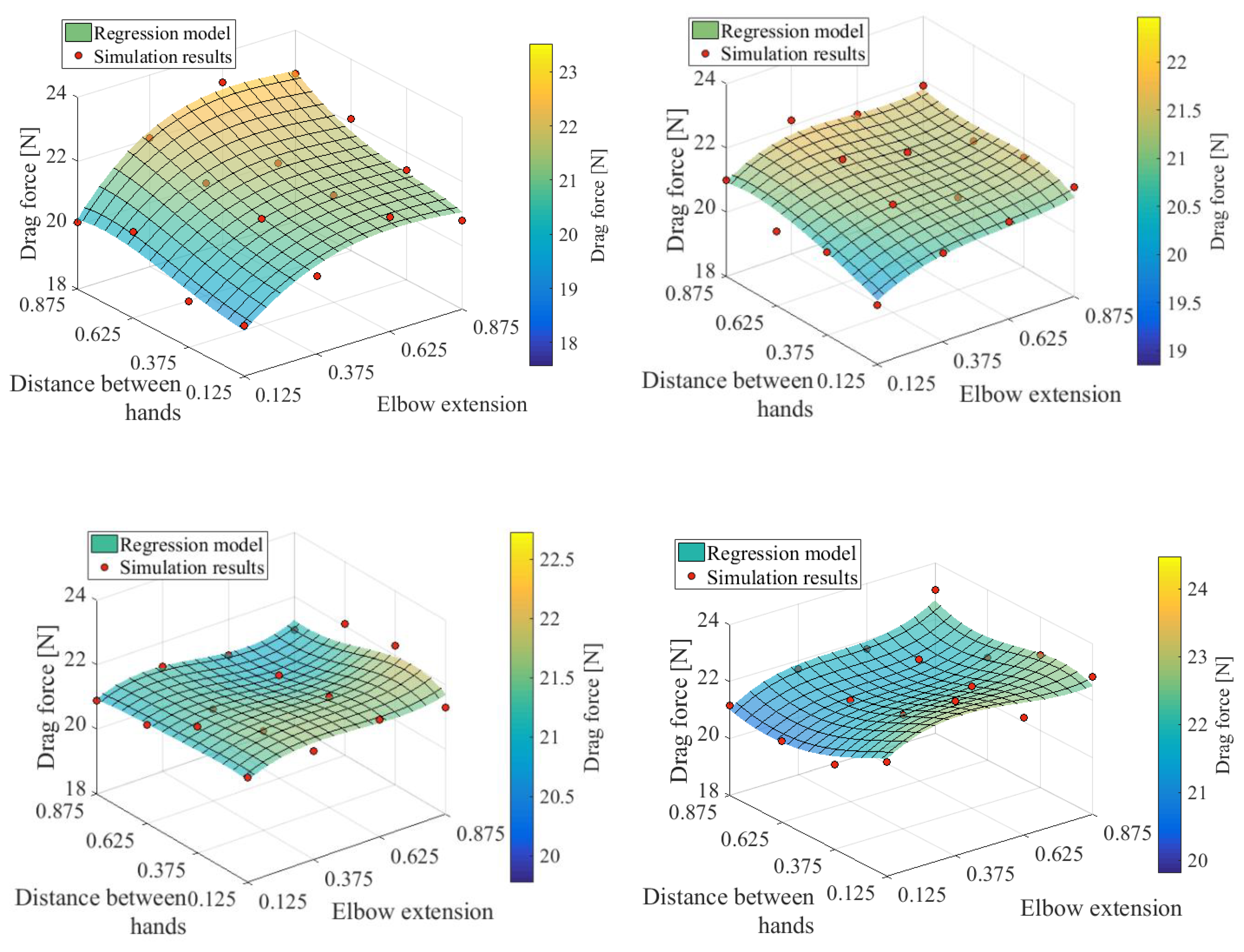
3.1. Overview of Drag Forces and Regression Model
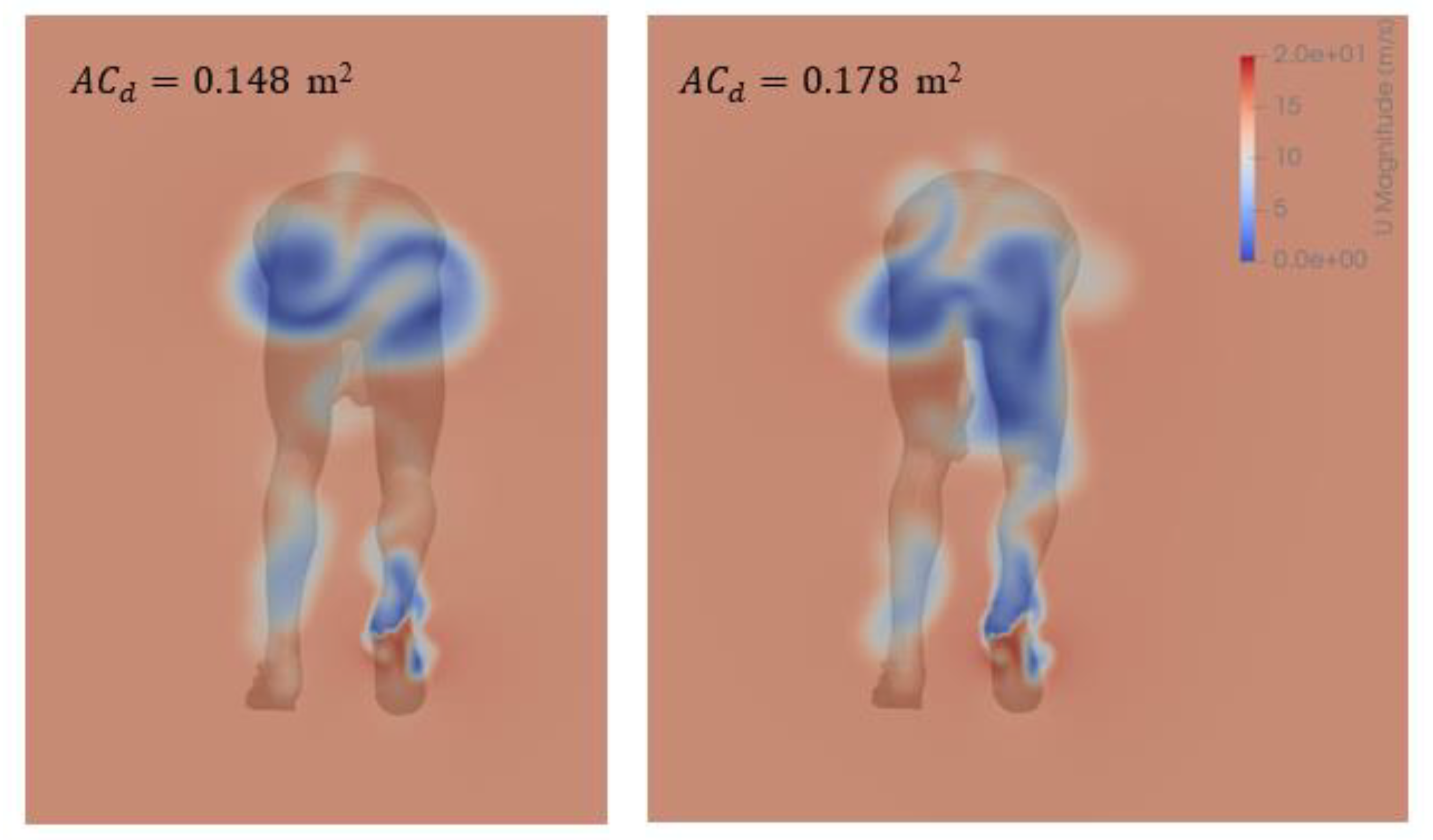
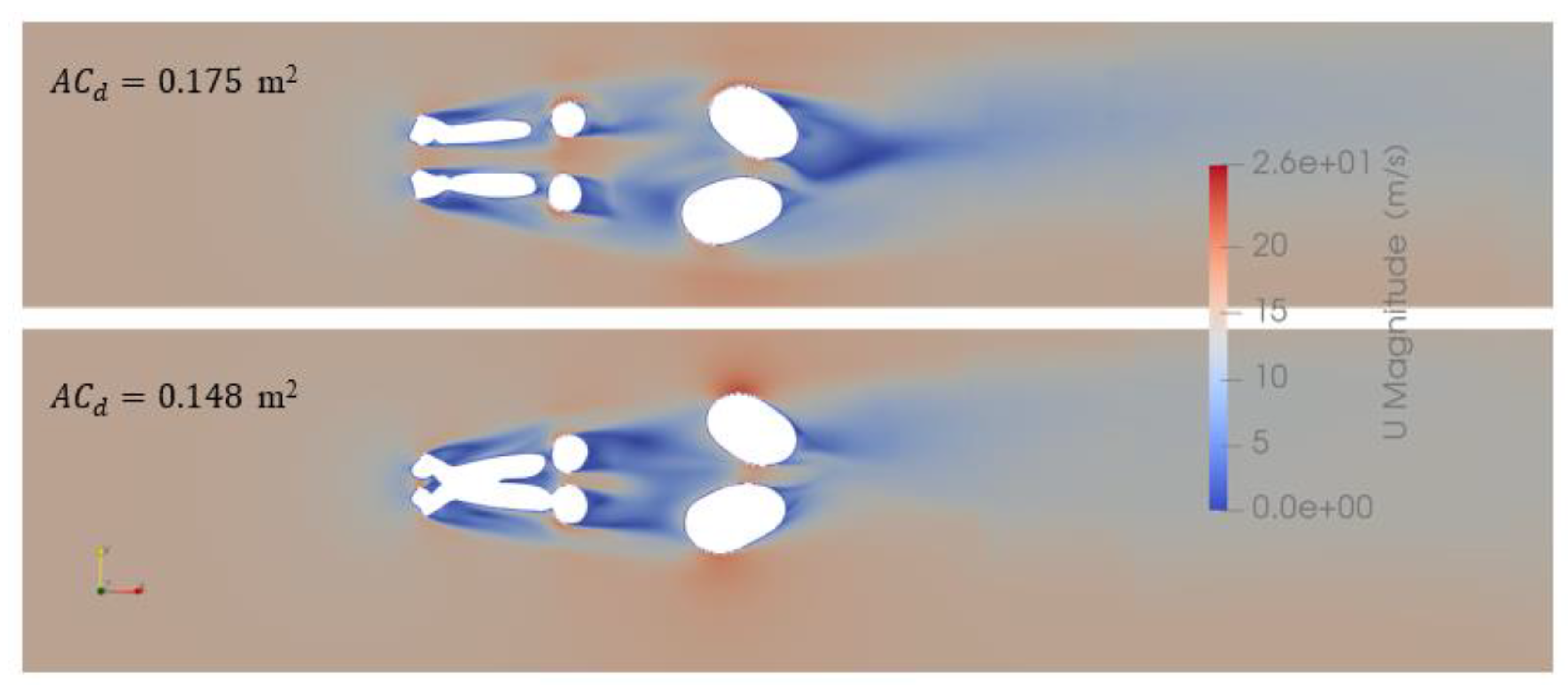
3.2. Influence of Elbow Extension
3.3. Influences of Shoulder Abduction and Elbow Rotation
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Grappe, F.; Candau, R.; Belli, A.; Rouillon, J.D. Aerodynamic drag in field cycling with special reference to the Obree’s position. Ergonomics 1997, 40, 1299–1311. [Google Scholar] [CrossRef]
- Defraeye, T.; Blocken, B.; Koninckx, E.; Hespel, P.; Carmeliet, J. Aerodynamic study of different cyclist positions: CFD analysis and full-scale wind-tunnel tests. J. Biomech. 2010, 43, 1262–1268. [Google Scholar] [CrossRef] [PubMed]
- García-López, J.; Rodríguez-Marroyo, J.A.; Juneau, C.E.; Peleteiro, J.; Martínez, A.C.; Villa, J.G. Reference values and improvement of aerodynamic drag in professional cyclists. J. Sports Sci. 2008, 26, 277–286. [Google Scholar] [CrossRef] [PubMed]
- Beaumont, F.; Taiar, R.; Polidori, G.; Trenchard, H.; Grappe, F. Aerodynamic study of time-trial helmets in cycling racing using CFD analysis. J. Biomech. 2018, 67, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Blocken, B.; Defraeye, T.; Koninckx, E.; Carmeliet, J.; Hespel, P. CFD simulations of the aerodynamic drag of two drafting cyclists. Comput. Fluids 2013, 71, 435–445. [Google Scholar] [CrossRef]
- Internationale, UC. Clarification Guide of the UCI Technical Regulation. In: Internationale UC, (ed.). 4/5/2020 ed.: Union Cycliste Internationale, 2020.
- Weller, H.G.; Tabor, G.; Jasak, H.; Fureby, C. A tensorial approach to computational continuum mechanics using object-oriented techniques. Comput. Phys. 1998, 12, 620–631. [Google Scholar] [CrossRef]
- Menter, F.R.; Kuntz, M.; Langtry, R. Ten years of industrial experience with the SST turbulence model. In Proceedings of the fourth international symposium on turbulence, heat and mass transfer, Antalya, Turkey, 12–17 October 2003; pp. 625–632. [Google Scholar]
- Mannion, P.; Toparlar, Y.; Blocken, B.; Hajdukiewicz, M.; Andrianne, T.; Clifford, E. Improving CFD prediction of drag on Paralympic tandem athletes: influence of grid resolution and turbulence model. Sports Eng. 2018, 21(2), 1–13. [Google Scholar] [CrossRef]
- Crouch, T.N.; Burton, D.; Brown, N.A.T.; Thompson, M.C.; Sheridan, J. Flow topology in the wake of a cyclist and its effect on aerodynamic drag. J. Fluid Mech. 2014, 748, 5–35. [Google Scholar] [CrossRef]
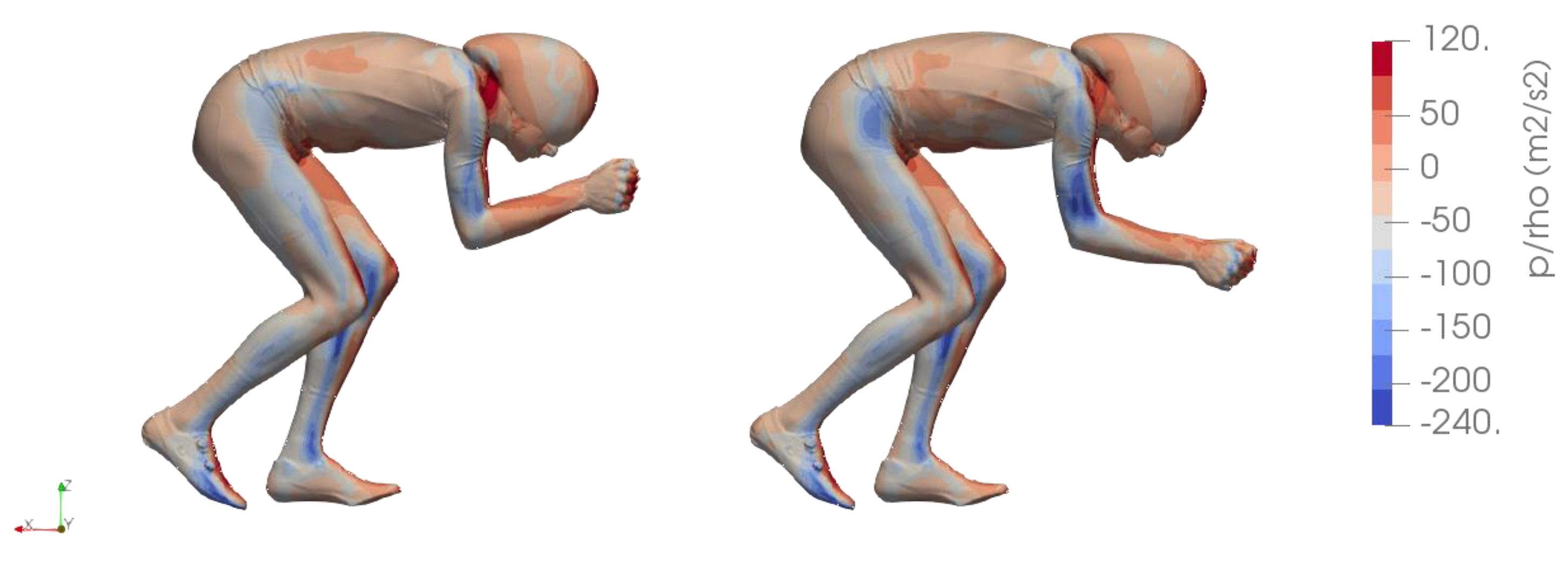
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giljarhus, K.E.T.; Stave, D.Å.; Oggiano, L. Investigation of Influence of Adjustments in Cyclist Arm Position on Aerodynamic Drag Using Computational Fluid Dynamics. Proceedings 2020, 49, 159. https://doi.org/10.3390/proceedings2020049159
Giljarhus KET, Stave DÅ, Oggiano L. Investigation of Influence of Adjustments in Cyclist Arm Position on Aerodynamic Drag Using Computational Fluid Dynamics. Proceedings. 2020; 49(1):159. https://doi.org/10.3390/proceedings2020049159
Chicago/Turabian StyleGiljarhus, Knut Erik Teigen, Daniel Årrestad Stave, and Luca Oggiano. 2020. "Investigation of Influence of Adjustments in Cyclist Arm Position on Aerodynamic Drag Using Computational Fluid Dynamics" Proceedings 49, no. 1: 159. https://doi.org/10.3390/proceedings2020049159
APA StyleGiljarhus, K. E. T., Stave, D. Å., & Oggiano, L. (2020). Investigation of Influence of Adjustments in Cyclist Arm Position on Aerodynamic Drag Using Computational Fluid Dynamics. Proceedings, 49(1), 159. https://doi.org/10.3390/proceedings2020049159



