Investigating the Influence of Shaft Balance Point on Clubhead Speed: A Simulation Study †
Abstract
1. Introduction
2. Materials and Methods
2.1. Shaft Modeling
2.2. Golfer Model
2.3. Golf Swing Optimization
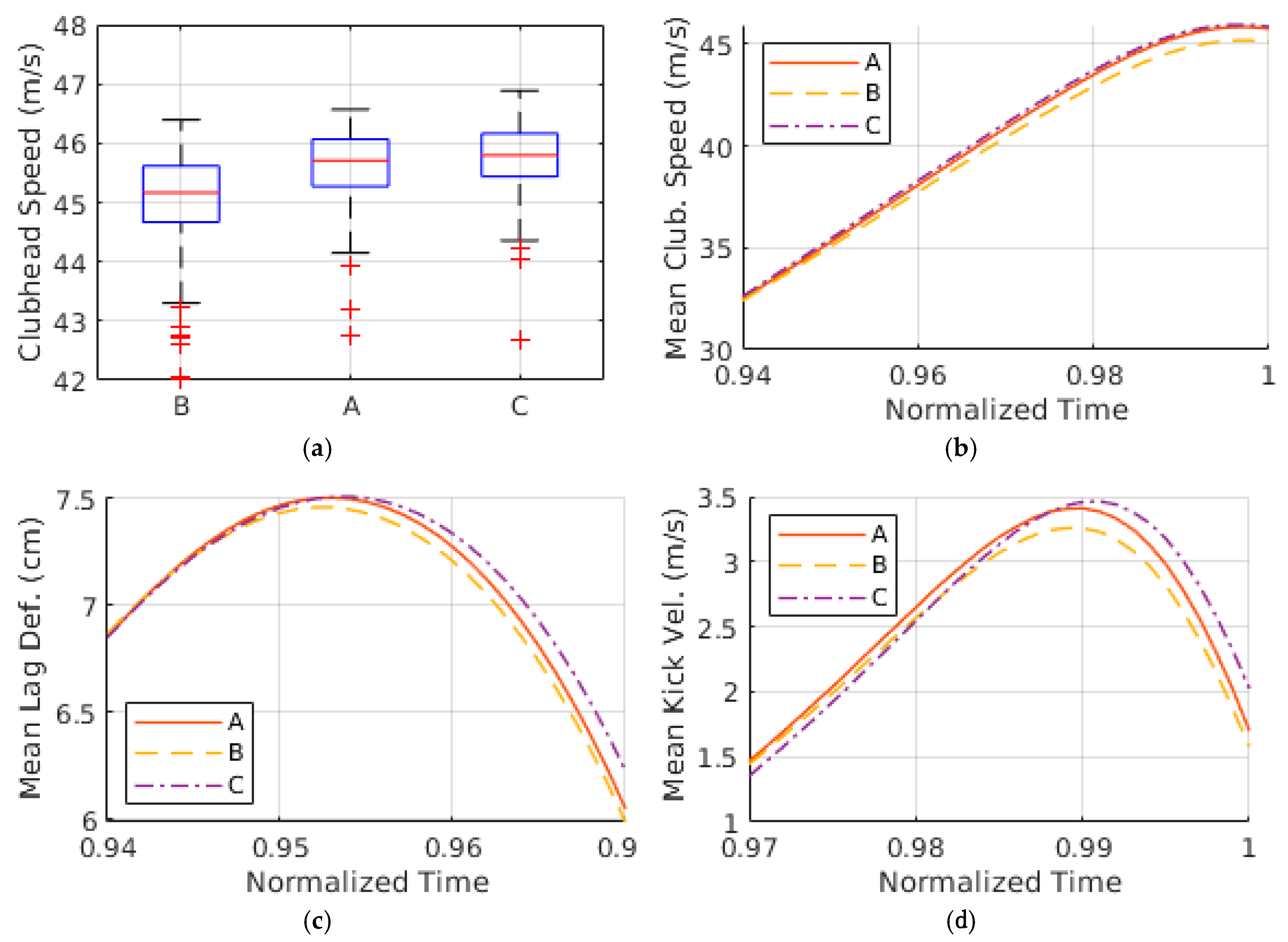
3. Results
4. Discussion
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- MacKenzie, S.J.; Sprigings, E.J. Understanding the role of shaft stiffness in the golf swing. Sports Eng. 2009, 12, 13–19. [Google Scholar] [CrossRef][Green Version]
- Betzler, N.F.; Monk, S.A.; Wallace, E.S.; Otto, S.R. Effects of golf shaft stiffness on strain, clubhead presentation and wrist kinematics. Sports Biomech. 2012, 11, 223–238. [Google Scholar] [CrossRef] [PubMed]
- MacKenzie, S.J.; Boucher, D.E. The influence of golf shaft stiffness on grip and clubhead kinematics. J. Sports Sci. 2017, 35, 105–111. [Google Scholar] [CrossRef] [PubMed]
- Jones, K.M.; Betzler, N.F.; Wallace, E.S.; Otto, S.R. Differences in shaft strain patterns during golf drives due to stiffness and swing effects. Sports Eng. 2019, 22. [Google Scholar] [CrossRef]
- Pelz, D. A simple, scientific, shaft test: Steel versus graphite. In Science and Golf: Proceedings of the First World Scientific Congress of Golf; Cochran, A.J., Ed.; Spon: London, UK, 1990. [Google Scholar]
- Sprigings, E.J.; Neal, R.J. An insight into the importance of wrist torque in driving the golfball: A simulation study. J. Appl. Biomech. 2000, 16, 356–366. [Google Scholar] [CrossRef]
- Mackenzie, S.J.; Sprigings, E.J. A three-dimensional forward dynamics model of the golf swing. Sports Eng. 2009, 11, 165–175. [Google Scholar] [CrossRef]
- Balzerson, D.; Banerjee, J.; McPhee, J. A three-dimensional forward dynamic model of the golf swing optimized for ball carry distance. Sports Eng. 2016, 16, 237–250. [Google Scholar] [CrossRef]
- McNally, W.; McPhee, J. Dynamic optimization of the golf swing using a six degree-of-freedom biomechanical model. In Proceedings of the 12th Conference of the International Sports Engineering Association, Brisbane, QLD, Australia, 26–28 March 2018. [Google Scholar]
- McNally, W.; Henrikson, E.; McPhee, J. A continuous analytical shaft model for fast dynamic simulation of the golf swing. Sports Eng. 2019. [Google Scholar] [CrossRef]
- Betzler, N.F.; Slater, C.; Strangwood, M.; Monk, S.A.; Otto, S.R.; Wallace, E.S. The static and dynamic stiffness behaviour of composite golf shafts and their constituent materials. Sports Eng. 2011, 14. [Google Scholar] [CrossRef]
- Petersen, W.; McPhee, J. Comparison of impulse-momentum and finite-element models for impact between golf ball and clubhead. In Science and Golf V: Proceedings of the World Scientific Congress of Golf; Crews, D., Lutz, R., Eds.; Energy in Motion: Mesa, AZ, USA, 2008. [Google Scholar]
- Quintavalla, S.J. A generally applicable model for the aerodynamic behavior of golf balls. In Science and Golf IV: Proceedings of the World Scientific Congress of Golf; Thain, E., Ed.; Routledge: Abingdon-on-Thames, UK, 2012. [Google Scholar]
- Werner, F.D.; Grieg, R.C. How Golf Clubs Really Work and How to Optimize Their Design; Origin Inc, 2000. [Google Scholar]
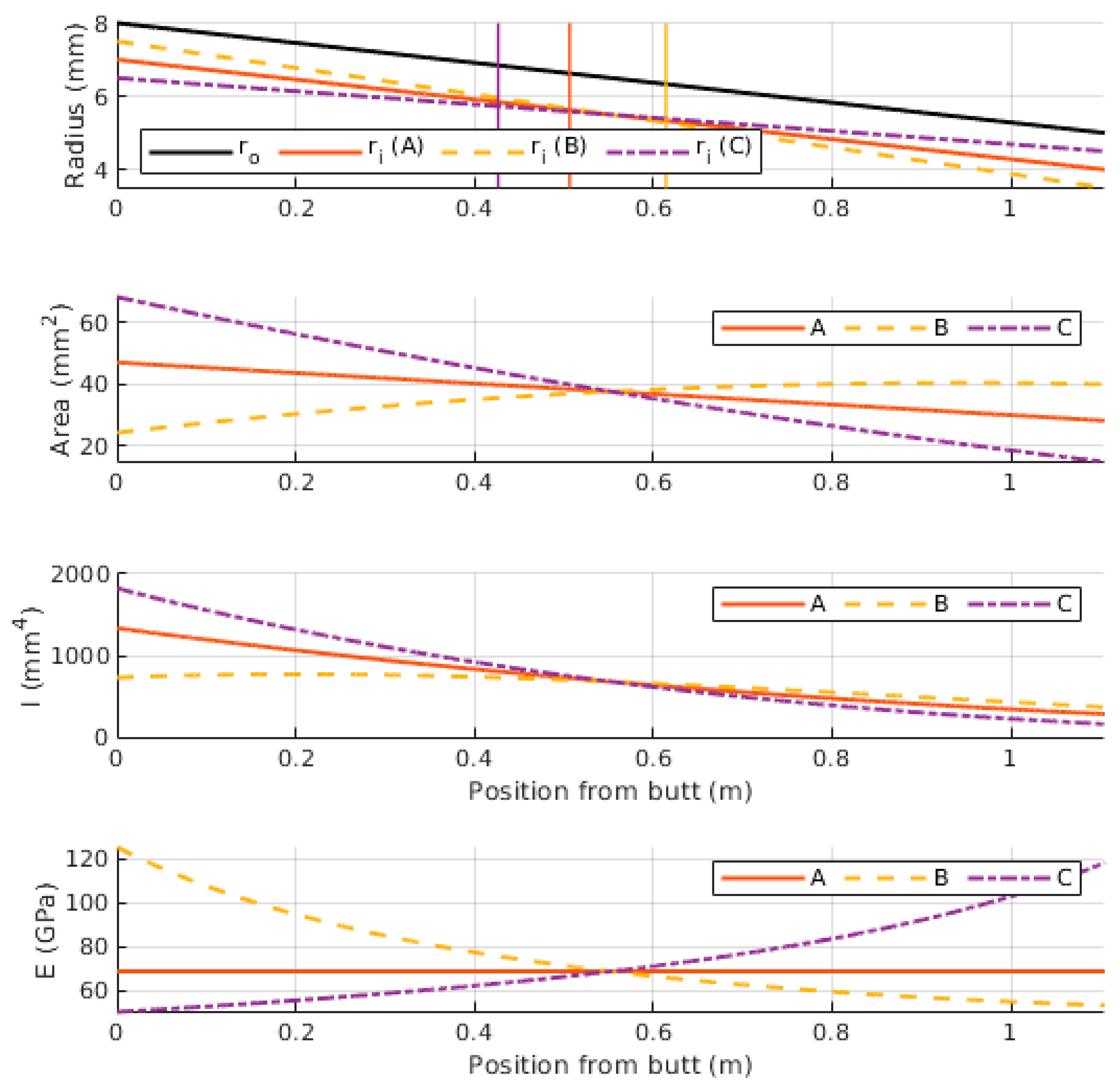
| Shaft | |||||
|---|---|---|---|---|---|
| A | 1 | 0 | 0.5064 | 23.17 | 1.561 |
| B | 0.5 | 1 | 0.6143 | 31.10 | 1.897 |
| C | 1.5 | -1 | 0.4264 | 17.58 | 1.508 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
McNally, W.; McPhee, J. Investigating the Influence of Shaft Balance Point on Clubhead Speed: A Simulation Study. Proceedings 2020, 49, 156. https://doi.org/10.3390/proceedings2020049156
McNally W, McPhee J. Investigating the Influence of Shaft Balance Point on Clubhead Speed: A Simulation Study. Proceedings. 2020; 49(1):156. https://doi.org/10.3390/proceedings2020049156
Chicago/Turabian StyleMcNally, William, and John McPhee. 2020. "Investigating the Influence of Shaft Balance Point on Clubhead Speed: A Simulation Study" Proceedings 49, no. 1: 156. https://doi.org/10.3390/proceedings2020049156
APA StyleMcNally, W., & McPhee, J. (2020). Investigating the Influence of Shaft Balance Point on Clubhead Speed: A Simulation Study. Proceedings, 49(1), 156. https://doi.org/10.3390/proceedings2020049156





