Kinematic Analysis of Figure Skating Jump by Using Wearable Inertial Measurement Units ^†

Abstract

The purpose of this study was to demonstrate the feasibility of measuring and analyzing characteristics of figure skating jumps using wearable sensors. One elite figure skater, outfitted with five inertial measurement units (IMUs), performed flip jumps with single, double, and triple revolutions. Take-off event and flight phase of each trial were under analysis. Kinematic differences among jumps with variant revolutions as well as key factors for performing successfully landed triple jumps were determined by IMU signals. Compared with a video-based method, this study revealed the following characteristics that coincide with previous studies: at take-off event, the skater performed pre-rotation and took off with preferred postural positions as revolutions increased (p < 0.01); during flight, the skater struggled more to maintain the smallest inertial of moment as revolutions increased (p < 0.01); in order to perform successfully landed jumps, it was crucial that the skater improved the control of preparation for flight at take-off (p < 0.05).

1. Introduction

Jumps are the most important technical element in figure skating competitions on account of their large proportion during the program and high basic value in discipline. Jump techniques have been so advanced these days that jumps with more than triple revolutions are performed widely by both male and female skaters in international competitions. Several studies have been conducted for kinematic analysis of figure skating jumps by using video-based motion capture. These studies have reported several kinematic differences among jumps with single, double, and triple revolutions [1,2,3,4,5].

Studies on the major difference in the successful and unsuccessful jumps has not been sufficiently made [5]. Particularly, the function of co-movement among body segments during successful jumps is confined. Recently, a requirement was raised for real-time feedback and automatic coaching during on-ice jump training [6]. However, video-based quantifying for kinematic characteristics has its own limitations due to the non-real-time analysis, as well as the uncertain results interfered by the environmental light.

A sensor-based method was used in a previous study to estimate the skaters’ training condition by a single inertial measurement unit (IMU), rather than to quantify (as well as analyze) the skaters’ jump techniques [7]. Thus, in this study, we used a sensor-based analysis to determine significant kinematic differences among jumps with variant revolutions, as well as key factors for performing successfully landed triple jumps. The purpose of this study was to demonstrate the feasibility of measuring and analyzing characteristics of figure skating jumps using wearable sensors.

2. Materials and Methods

2.1. Participant

The study was conducted with the assistance of Waseda University figure skating club (Saitama, Japan). One nationally ranked competitive male figure skater participated in the study to perform single, double, and triple flip jumps.

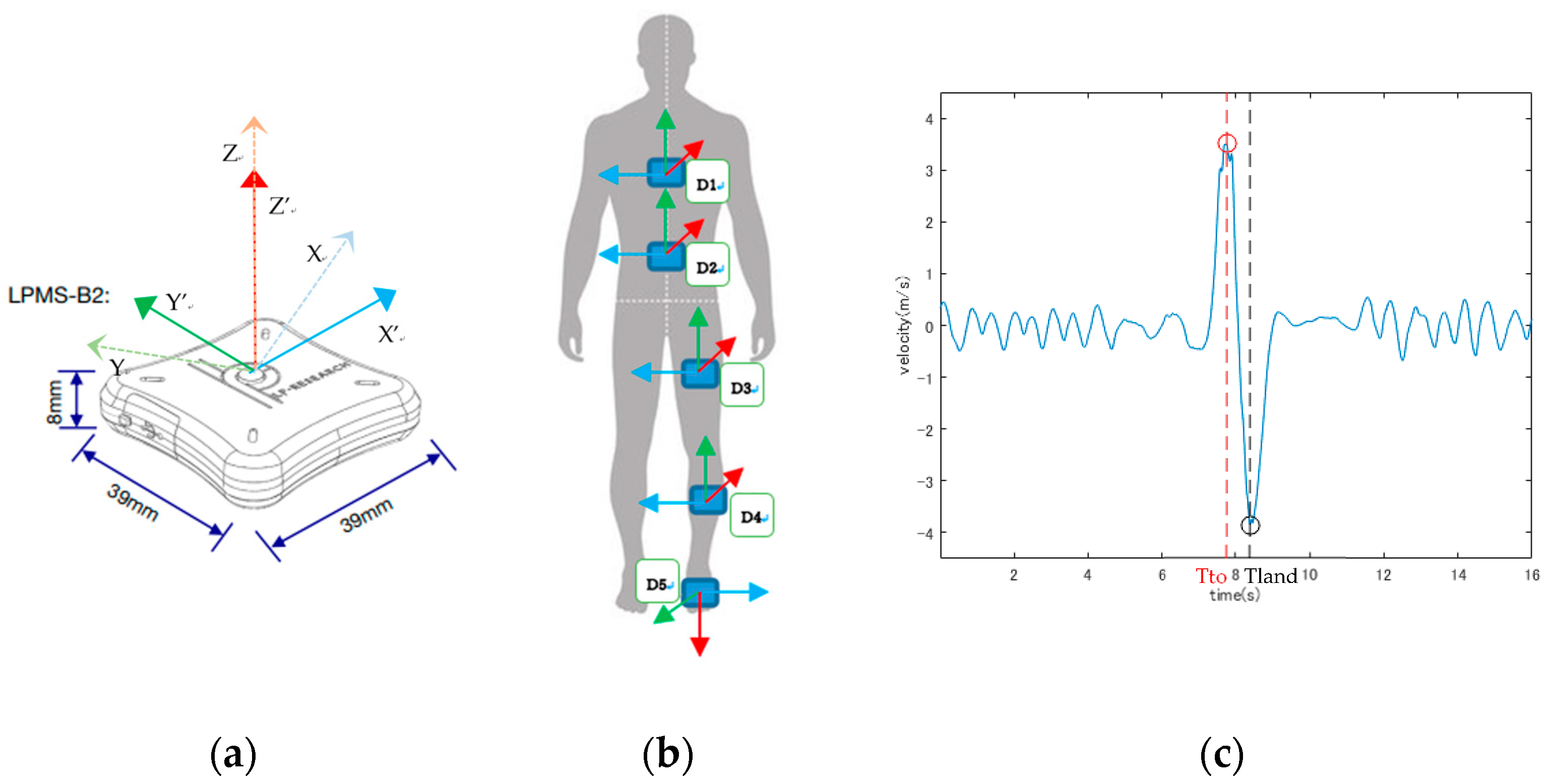
2.2. Data Collection

Data collection consisted of three sections: single, double, and triple flip jumps. All data were collected simultaneously by five IMUs (product series: LPMS-B2, LP-Research, Tokyo, Japan) and six high-resolution cameras (FDR-AX100, SONY). Five IMUs were attached to the skater with a special uniform. Real-time sensor signals were recorded at the rate of 100 Hz by a mobile phone based on wireless transmission. Five body segments of the skater were outfitted with IMUs on the posterior side at the following approximately positions: the 2nd thoracic vertebra (D1), the 4th–5th lumbar vertebra (D2), the center of mass of left thigh (D3), the center of mass of left shank (D4), and mid-sole of the left skate boot (D5; Figure 1b). Sensor coordinate system S (X’Y’Z’) was aligned with the global coordinate system G (XYZ) automatically based on gravity and magnetic field (Figure 1a). Six high-speed cameras were placed around the ice rink to record video data at a frame rate of 60 fps to be used as reference.

The skater warmed up both off-ice and on-ice for a total of 20 minutes, then performed seven single, fourteen triple, and nine double flip jumps successively. The received signals of triple jumps included nine successful jumps (3Fo), which were trials that landed clearly on the right outside edge, three unsuccessful jumps (3Fx), which are trials that landed with the center of mass of the body deviating from landing leg (landed two-foot, stepped out, and fell), as well as two popped jumps (3Fp), which are trials that performed with fewer rotations than intended (single rotation in these two cases). All received single (1F) and double signals (2F) were classified as successful trials.

2.3. Data Processing

Data processing was performed by MATLAB R2017a. In this study, kinematic parameters at take-off event and during the flight phase were calculated from raw signals. Raw signals consisted of three parts: angular velocity (degree/s), Euler angle (degree), and linear acceleration (g) [8]. These signals were filtered by Butterworth low-pass filter with cut-off frequency of 10 Hz. Then linear acceleration expressed in coordinate system S from D2, which was attached approximately to the center of mass of the body, was transformed to be expressed in coordinate system G by using Euler rotation matrix. Euler rotation sequence was set with the order of X’Y’Z’ in LPMS-B2. Since the indoor environment and mobile phone signal interfered with magnetometer during coordinate system alignment, only Z’-axis direction was precisely aligned to the vertical, upward Z-axis direction based on gravity (Figure 1a); vertical velocity (VV), which was the value of Z-axis velocity in coordinate system G, was acquired using rotation matrix with incomplete X’Y’ Euler rotation sequence to transform velocity vector from coordinate system S to coordinate system G. Firstly, D2 velocity in coordinate system S was obtained by numerically integrating D2 linear acceleration after removing the moving average in order to minimize the integral drift. Then the transformation of velocity vector between coordinate systems was conducted using incomplete rotation matrix:

$$\left[\begin{array}{c}{\mathit{v}}_{\mathit{X}-\mathit{Y}}\\ {\mathit{v}}_{\mathit{Y}-\mathit{X}}\\ {\mathit{v}}_{\mathit{Z}}\end{array}\right]=\left[\begin{array}{ccc}\mathit{c}\mathit{o}\mathit{s}{\mathbf{\theta }}_{\mathit{Y}’}& \mathbf{0}& \mathit{s}\mathit{i}\mathit{n}{\mathbf{\theta }}_{\mathit{Y}’}\\ \mathbf{0}& \mathbf{1}& \mathbf{0}\\ -\mathit{s}\mathit{i}\mathit{n}{\mathbf{\theta }}_{\mathit{Y}’}& \mathbf{0}& \mathit{c}\mathit{o}\mathit{s}{\mathbf{\theta }}_{\mathit{Y}’}\end{array}\right]·\left[\begin{array}{ccc}\mathbf{1}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& \mathit{c}\mathit{o}\mathit{s}{\mathbf{\theta }}_{\mathit{X}’}& -\mathit{s}\mathit{i}\mathit{n}{\mathbf{\theta }}_{\mathit{X}’}\\ \mathbf{0}& \mathit{s}\mathit{i}\mathit{n}{\mathbf{\theta }}_{\mathit{X}’}& \mathit{c}\mathit{o}\mathit{s}{\mathbf{\theta }}_{\mathit{X}’}\end{array}\right]·\left[\begin{array}{l}{\mathit{v}}_{\mathit{X}’}\\ {\mathit{v}}_{\mathit{Y}’}\\ {\mathit{v}}_{\mathit{Z}’}\end{array}\right]$$

(1)

where $v_{X-Y}$ and $v_{Y-X}$ are velocity components in two orthogonal directions in X-Y plane of coordinate system G; $v_Z$ is Z-axis velocity component in coordinate system G; $v_{X’}$, $v_{Y’}$, and $v_{Z’}$ are X’-axis, Y’-axis and Z’-axis velocity components in coordinate system S, respectively; ${\theta }_{X’}$, and ${\theta }_{Y’}$ are X’-axis and Y’-axis Euler angles, respectively. The value of $v_Z$ was defined as VV. In this study, none of Y’-axis rotations of IMUs exceeding the range of −89 to 89 degrees avoided singularity problem. The moment when vertical velocity reached maximum value was defined as take-off event (Tto), and the moment of minimum was defined as landing event (Tland) for all trials. The time interval between Tto and Tland was defined as flight phase. Flight time (FT) was calculated as Tland-Tto (Figure 1c). Video data was used to obtain the time interval between take-off and landing events as the gold standard for FT. Percent root-mean-square error (RMSE%) between gold standard FT and FT derived from D2 signals was computed for 1F, 2F, 3Fo, 3Fx, and 3Fp by the following formula:

$$\mathit{R}\mathit{M}\mathit{S}\mathit{E}\%=\mathbf{100}\%·\frac{\sqrt{\frac{\mathbf{1}}{\mathit{n}}{{\displaystyle \sum }}_{\mathit{i}=\mathbf{1}}^{\mathit{n}}{\left({\mathit{y}}_{\mathit{i}}-\widehat{{\mathit{y}}_{\mathit{i}}}\right)}^{\mathbf{2}}}}{\overline{\mathit{y}}}$$

(2)

where n is the number of 1F, 2F, 3Fo, 3Fx, and 3Fp trials; $y_i$ and $\widehat{y_i}$ are the $i$th values of D2 signal FT and gold standard FT, respectively; $\overline{y}$ is the arithmetic mean of $y_i$values. The RMSE% results were 5.97%, 5.79%, 11.82%, 9.14%, and 10.49% for 1F, 2F, 3Fo, 3Fx, and 3Fp, respectively.

Subsequently, seven kinematic parameters of the center of mass of the body were derived as follows:

• Horizontal velocity (HV): horizontal component of velocity at Tto, calculated using magnitude of resultant velocity and VV from D2.
• Flight Height (FH): maximum height during flight phase, calculated using FT from D2 ($g·{\mathrm{FT}}^2/8$, where $g$ is the acceleration of gravity).
• Take-off angle (ToA): angle between the resultant velocity vector and the horizontal plane at Tto, calculated using the magnitude of VV and HV from D2.
• Take-off Tilt (ToT): relative angle between longitude axis of the body (Y’-axis of D2) and the vertical axis (Z-axis) at Tto, calculated using X’-axis Euler angle from D2.
• Time to the tightest position (TtoTP): time to the moment when the skater achieved his maximum rotation speed during flight phase from Tto, calculated using Y’-axis angular velocity from D2.
• Revolutions in the air (RinA): revolutions performed during flight time, calculated using Z’-axis Euler angle from D2.
• Angular velocity (AV): average angular velocity during flight phase, calculated using RinA and FT.

Another four kinematic parameters derived from body segments were computed to determine the co-movement within body. These parameters are differences of angular velocity between thorax and pelvis (DiffAV(tho-pel)), pelvis and thigh (DiffAV(pel-thi)), thigh and shank (DiffAV(thi-sha)), as well as shank and sole (DiffAV(sha-sol)), calculated by subscribing Z-axis angular velocity expressed in coordinate system G from two adjacent IMUs.

2.4. Statistical Analysis

Statistical analysis was conducted by R Studio. A non-parametric Welch’s Heteroscedastic F-test was conducted with the same parameters for the 1F, 2F, and 3F trials to find the difference between variance rotations jumps [9]. Furthermore, a two sample t-test was conducted between 3Fo and 3Fx to find the key factors for successful triple flip jumps. Two trials of 3Fp were excluded from statistical analysis due to an insufficient sample size. Prior to the statistical test, all groups were determined by whether the samples were normally distributed by performing a Shapiro–Wilk normality test. Consequentially, a Bartlett test of homogeneity of variances was performed to determine whether the variances were the same among the groups compared. Statistical significance level was set to 0.05.

3. Results

Table 1. Kinematic parameters for 1F, 2F and 3Fo (Mean ± Standard deviation). parameters highlighted were found significant different among 1F, 2F and 3Fo (see definition of 1F, 2F and 3Fo in Section 2.2; see definition of all thirteen kinematic parameters in Section 2.3).

	FT (s)	VV (m/s)	FH (m)	AV (Degree/s)	HV (m/s)
1F	0.48 ± 0.01 †††	1.94 ± 0.24 †††	0.28 ± 0.01 †††	399.81 ± 26.31 †††	4.31 ± 0.18 †††
2F	0.54 ± 0.03 ***	3.35 ± 0.11 ***	0.36 ± 0.03 ***	849.48 ± 35.65 ***	2.78 ± 0.27 ***
3Fo	0.62 ± 0.07 ⋇⋇	3.71 ± 0.24 ⋇⋇⋇	0.48 ± 0.10 ⋇⋇	1071.44 ± 47.00 ⋇⋇⋇	2.97 ± 0.98
	ToA (Degree)	ToT (Degree)	TtoTP (s)	RinA (Revolution)
1F	25.17 ± 2.53 †††	50.19 ± 5.77 †††	0.08 ± 0.09 †††	0.53 ± 0.03 †††
2F	49.74 ± 2.44 ***	38.65 ± 7.81 **	0.20 ± 0.05 **	1.28 ± 0.08 ***
3Fo	51.45 ± 9.56	32.08 ± 12.61	0.42 ± 0.08 ⋇⋇⋇	1.84 ± 0.13 ⋇⋇⋇
	DiffAV (tho-ple) (Degree/s)	DiffAV (ple-thi) (Degree/s)	DiffAV (thi-sha) (degree/s)	DiffAV (sha-sol) (degree/s)
1F	−826.51 ± 78.61▿	467.72 ± 116.10 ***	−195.75 ± 352.64	−169.78 ± 188.34
2F	−1056.52 ± 245.44	825.95 ± 151.25	−433.60 ± 99.95	−310.57 ± 197.13
3Fo	−1131.87 ± 381.82	749.55 ± 466.01	−286.65 ± 224.10	−308.92 ± 331.32

p < 0.03: ** 1F vs 2F, ⋇⋇ 2F vs 3Fo; p < 0.01: *** 1F vs 2F, ††† 1F vs 3Fo, ⋇⋇⋇ 2F vs 3Fo; p < 0.1: ▿1F vs 2F.

demonstrates an overview mean ± standard deviation for all thirteen kinematic parameters as well as the results of F-test among 1F, 2F, and 3Fo. Nine parameters derived from the center of mass of the body at Tto and during flight phase were observed to have significant statistical differences among 1F, 2F, and 3Fo. VV of 1F at Tto increased dramatically by 72.7% compared with 2F on average (p < 0.0001), whereas this increment was 10.7% from 2F to 3Fo (p = 0.006). AV during flight phase increased by 112.5% from 1F to 2F (p < 0.0001), 26.1% from 2F to 3Fo (p < 0.0001), and 168.0% from 1F to 3F (p < 0.0001). HV at Tto decreased by 35.50% from 1F to 2F (p < 0.0001) and 31.09% from 1F to 3Fo (p < 0.0001). ToA at Tto increased by 97.62% from 1F to 2F (p < 0.0001) and 104.41% from 1F to 3Fo (p = 0.01). ToT at Tto for 3Fo increased by 56.5% (p = 0.008), and in the case of 2F, increased by 29.9% (p = 0.01) on average when compared with 1F. Comparing TtoTP during flight phase, it takes the skater 0.42 s to hold his limbs close to the body to the tightest position in order to achieve his maximum angular velocity during performing a 3Fo, which was 67.7% of FT, while this duration was reduced by 52.4% on average in 2F (p < 0.0001), which was 37.0% of FT. Concerning 1F, TtoTP was approximately 0.08 s on average. RinA in the case of 3Fo showed as an average of 1.84, which was 61.3% of completed revolutions. Concerning 2F and 1F, RinA were 64.0% and 53% of completed revolutions. When comparing four kinematic parameters derived from body parts, DiffAV(tho-ple) and DiffAV(ple-thi) at Tto showed a significant difference between group 1F and 2F (p = 0.02; p = 0.0005).

Table 2. Kinematic parameters for 3Fo and 3Fx (Mean ± Standard deviation). Parameters highlighted were found significant different between 3Fo and 3Fx (see definition of 3Fo and 3Fx in Section 2.2; see definition of all thirteen kinematic parameters in Section 2.3).

	FT (s)	VV (m/s)	FH (m)	AV (Degree/s)	HV (m/s)
3Fo	0.62 ± 0.07	3.71 ± 0.24	0.48 ± 0.10	1071.44 ± 47.00	2.97 ± 0.98
3Fx	0.53 ± 0.04	3.77 ± 0.41	0.34 ± 0.05	1048.22 ± 119.27	2.91 ± 0.97
	ToA (degree)	ToT (degree)	TtoTP (s)	RinA (revolution)
3Fo	51.45 ± 9.56	32.08 ± 12.61	0.42 ± 0.08	1.84 ± 0.13
3Fx	25.17 ± 2.53	51.64 ± 14.29	0.37 ± 0.06	1.67 ± 0.07
	DiffAV(tho-ple) (Degree/s)	DiffAV(ple-thi) (Degree/s)	DiffAV (thi-sha) (Degree/s)	DiffAV(sha-sol) (Degree/s)
3Fo	−1131.87 ± 381.82	749.55 ± 466.01	−286.65 ± 224.10	−308.92 ± 331.32
3Fx	−805.58 ± 342.48	960.58 ± 401.46	−708.82 ± 294.10	−306.89 ± 435.55

p < 0.05; p < 0.1.

demonstrates an overview mean ± standard deviation for all thirteen kinematic parameters of 3Fo and 3Fx, as well as results of t-test between these two groups. FT, FH, and ToT at Tto were found significant differences between successful and unsuccessful landed triple flips. Fewer RinA during flight phase was observed in 3Fx, which was 1.67 compared with 1.84 for 3Fo (p = 0.056). Conversely, ToT at Tto was 61.0% larger than 32.08 degrees for 3Fo (p = 0.047).

4. Discussion

In this study, we used sensor-based analysis to determine significant kinematic differences amongst jumps with variant revolutions, as well as key factors for performing successfully landed triple jumps. The purpose of this study was to demonstrate the feasibility of measuring and analyzing characteristics of figure skating jumps using wearable sensors.

According to conclusions drawn in previous studies, vertical and angular momentum at take-off event are two key factors for jump techniques in figure skating [2,3,4]. The former results in a sufficient vertical velocity, accompanied by a sufficient flight time for skaters to complete revolutions in the air by generating a jump height calculating by $g·{\mathrm{FT}}^2/8$. The latter guarantees a great angular velocity for body rotations [1,2,3,4,5]. Some previous studies comparing multi-revolutions axel jumps observed no differences in vertical velocity, flight time, and jump height among single, double, and triple axels. Consequently, skaters were considered to complete more revolutions solely by a greater angular velocity [1,2]. In contrast, studies comparing multi-revolution jump take-offs from the backward edge, which is opposite to axel jumps that take-off from the forward edge, observed increments in all these four parameters as revolutions increased [3]. In this study, flip jump take-offs from backward edge showed consistent results in these four parameters with those backward take-off jumps in the previous studies, which indicated that the skater not only jumped higher but also rotated faster in order to complete more revolutions in the air. A possible explanation for constant vertical momentum in axel jumps is that it is more difficult to gain vertical velocity from “tangential motion” when performing axel jumps than performing other types. Tangential motion reported in the previous study is determined as an angular motion of toe-CM position vector, which was defined as a vector has terminal point at center of mass of the body and initial point at the toe of supporting leg) [1]. Due to the backward take-off and counterclockwise rotations in the air, jumps except axels are given a spare half pre-rotation on the ice prior to take-off. This half rotation probably enables skaters to generate more tangential motion on the ice, with a result that the tangential component of velocity increases easily. This spare half revolution can also be affirmed by RinA computed from IMU signals in this study. In triple, double, and single flips, the skater rotated in the air 61.3%, 64.0%, and 53.0% of completed revolutions respectively. Concluding from previous studies, approximately 78% (2.75 of 3.5 revolutions) of completed revolutions were performed in the air in a triple axel [1,4].

HV at Tto decreased from single to double and triple flips, accompanied by ToA increasing from single to double and triple flips, indicating that the skater improved the control of preparation for flight at take-off. ToT at Tto increased from triple to double as well as from double to single flips, indicating that the skater took off with a preferred postural position of the upper body while performing triple flips than double and single trials. During a high rated jump, tilt of the body was considered to decrease at the last contact with ice and then maintained a constant value of 10–15 degrees during flight phases [2,4]. As there are few opportunities for skaters to correct their flight position once they leave the ice into the air, this negative correlation between revolutions and ToT can be explained as the skater prepared more adequately for the best flight position in triple flip than in double and in single [4].

Furthermore, TtoTP was longer in triple flips than in double and in single trials in this study. Considering the faster angular velocity shown during the flight phase in triple flips, the centrifugal force accompanied by torso rotations was also theoretically greater in triple than in double and in single flips [2]. This is a possible explanation for a longer time to the tightest position in triple flips, since the skater had to resist a greater centrifugal force to maintain a tighter position in the air (a smaller moment of inertial), which as a consequence, reaches a faster angular velocity for more revolutions during the flight phase. As for kinematic parameters calculated from body segments, a difference in angular velocity between thorax and pelvis was found to vary between single and double flips. This indicates that possibly some co-ordination of motions existing among the upper and lower trunk at take-off varied between flip jumps with various revolutions. As for correlation between the movement of upper and lower body at take-off reported in previous studies [3], difference of angular velocity between pelvis and thigh was found to vary between single and double flips in this study, indicating that possible differences of co-movement exist between upper and lower body at take-off in flips with various revolutions. Since no statistical differences were verified between group 2F and 3F, as well as 1F and 3F, further consideration is necessary in future studies for more parameters calculated from body segments to determine the mechanism of co-movement among body segments when performing figure skating jumps.

ToT at Tto also showed smaller trends in successful trials compared to unsuccessful trials. Meanwhile, a slightly more RinA were performed for successful trials as well. Previous studies for successful and unsuccessful axel jumps reported greater pre-rotation at take-off and closer completing to landing in successful jumps [5], which can be explained as skaters intending to gain more controllable time prior to take-off and landing with more completed rotations, since it makes them match perfectly with the correct backward gliding direction after landing. In this study, ToT was smaller meaning also that during successful triple flips, the skater was in a better preparation position, which kept the upper body in a preferred postural position at the take-off event. In order to determine detailed information of the skater’s ability to control his take-off, quantifying for pre-rotation is critical.

5. Conclusions

In this study, we have presented a protocol of quantitative analysis for figure skating jumps based on multiple IMUs. This sensor-based analysis figured out kinematic significant differences among flip jumps with variant revolutions, as well as key factors for performing successfully landed triple flips. These experimental results showed that most of the kinematic characteristics coincided with those of previous video-based studies, which indicates that kinematic analysis based on IMUs provides feasibility to measure and analyze characteristics of figure skating jumps. Also, the IMU-based method we used allows real-time measurements and has potential to develop an automatic coaching system.