Impact Characteristics of a Badminton Racket with Realistic Finite Element Modeling ^†

Abstract

The tension of strings on a badminton racket can be adjusted by players according to their personal experiences. The best way to execute such an adjustment remains unclear. A finite element model was employed in this study to investigate the effect of having nonuniform string tension on string-bed deformation, and the direction of force applied to shuttlecock head upon impact. The racket model was based on a commercially available racket with a simplified string-bed of 16 strings established using SolidWorks. A displacement was applied to the ball to simulate impacting on the string-bed. The simulations revealed that slightly lowering the tension of off-centered strings had a minimal effect on the von Mises stress distribution of the ball and string-bed. The off-centered impact caused comparable contact force magnitude but altered force direction. Further investigation is needed for understanding the effect of varying string tension on badminton racket performance.

1. Introduction

Enhancing performance and reducing injury, as the main goals of athletes and coaches, can be achieved through research in sports biomechanics [1]. In addition to analyzing human movement kinetics/kinematics, applying material science and structural engineering to designing better equipment is also a growing field in sports biomechanics studies. There is no doubt that for sports activities in which a racket is held (e.g., tennis, badminton), the most important equipment is the racket itself. The most crucial performance factors of a racket are impact performance and control. The former refers to post-impact ball speed, which is described by the coefficient of restitution (COR). The latter refers to the accuracy of the landing after hitting the ball [2,3].

The mechanical property of the string-bed of a racket is key to athletic performance. How the strings affect the ball-racket impact requires in-depth investigation. The common practice of tennis/badminton racket stringing is to have a constant spring tension (in pounds) regardless of its length. This is questionable because theoretically the response to external loading (due to ball impact) is different for strings under the same tension but of different lengths [4]. Therefore, in considering minimum racket frame deformation and evenly distributed external loading, it is more plausible to allow the string tension to be adjusted based on its length.

The present study attempts to build a finite element model to simulate the impact between a shuttlecock and the string-bed of a badminton racket. Since the effect of having nonuniform string tension on racket performance remains unclear, the post-impact response is investigated by adjusting string tension. The simulation results will be helpful for performance enhancement by allowing the athletes to select and fine-tune the spring tension according to their needs.

2. Materials and Methods

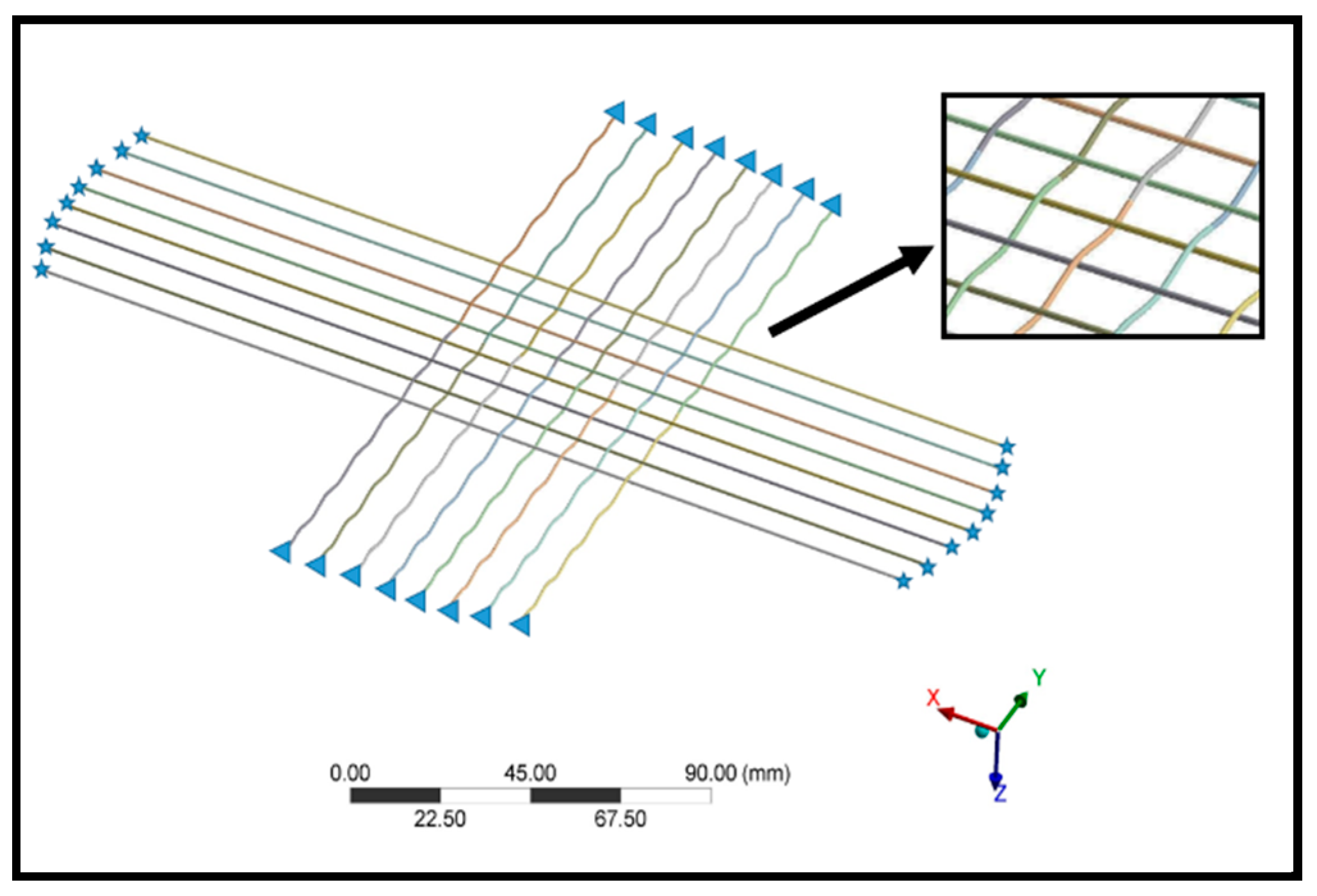
The finite element method was employed to evaluate von Mises stress distribution of the string-bed of a badminton racket upon ball impact. The lengths of the badminton racket strings were determined based on the commercially available Victor VS-800 with the length and width of the racket head being 253 mm and 188 mm, respectively (Figure 1). The diameter of the racket string was set at 0.7 mm. The Young’s modulus, Poisson’s ratio, and density of the string (made of Nylon) were 7200 MPa, 0.3, and 1100 kg/m³, respectively [5]. For simplicity, a half ball instead of a realistically modeled shuttlecock was used to simulate the impact on the string-bed consisting of 8 by 8 perpendicularly intertwined strings. The half-ball model has the same diameter (21 mm) as a real shuttlecock head. The material property of the strings and the ball was assumed to be linear, isotropic, and homogeneous. According to ANSYS database, the Young’s modulus, Poisson’s ratio, and density of the half-ball model (made of structural steel) were 200,000 MPa, 0.3, and 7850 kg/m³, respectively.

The ANSYS workbench was used for mesh generation and model simulation. The triangle mesh type was employed for the ball and strings with an element size of 3 and 0.4 mm, respectively. Furthermore, nonlinear contact (frictional contact) was applied between all strings. The string–string and ball–string friction coefficient were assumed to be 0.1 [5]. The positions of both ends of each string were fixed. A 5 mm displacement was applied to the ball to simulate impacting on the string-bed. To reduce computation error due to model nonlinearity, the simulation was divided into three steps. The tension was applied to strings first in the longitudinal (X) direction, and then to strings in the medial-lateral (Y) direction. Finally, the ball was displaced to impact the string-bed.

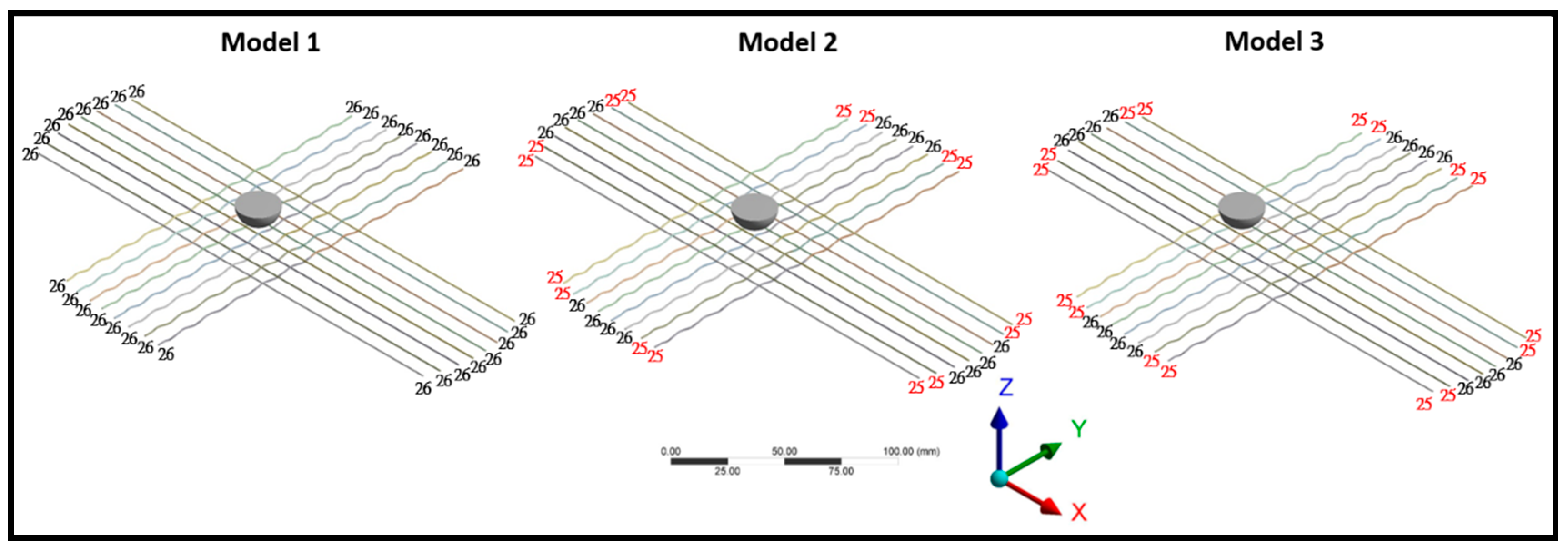
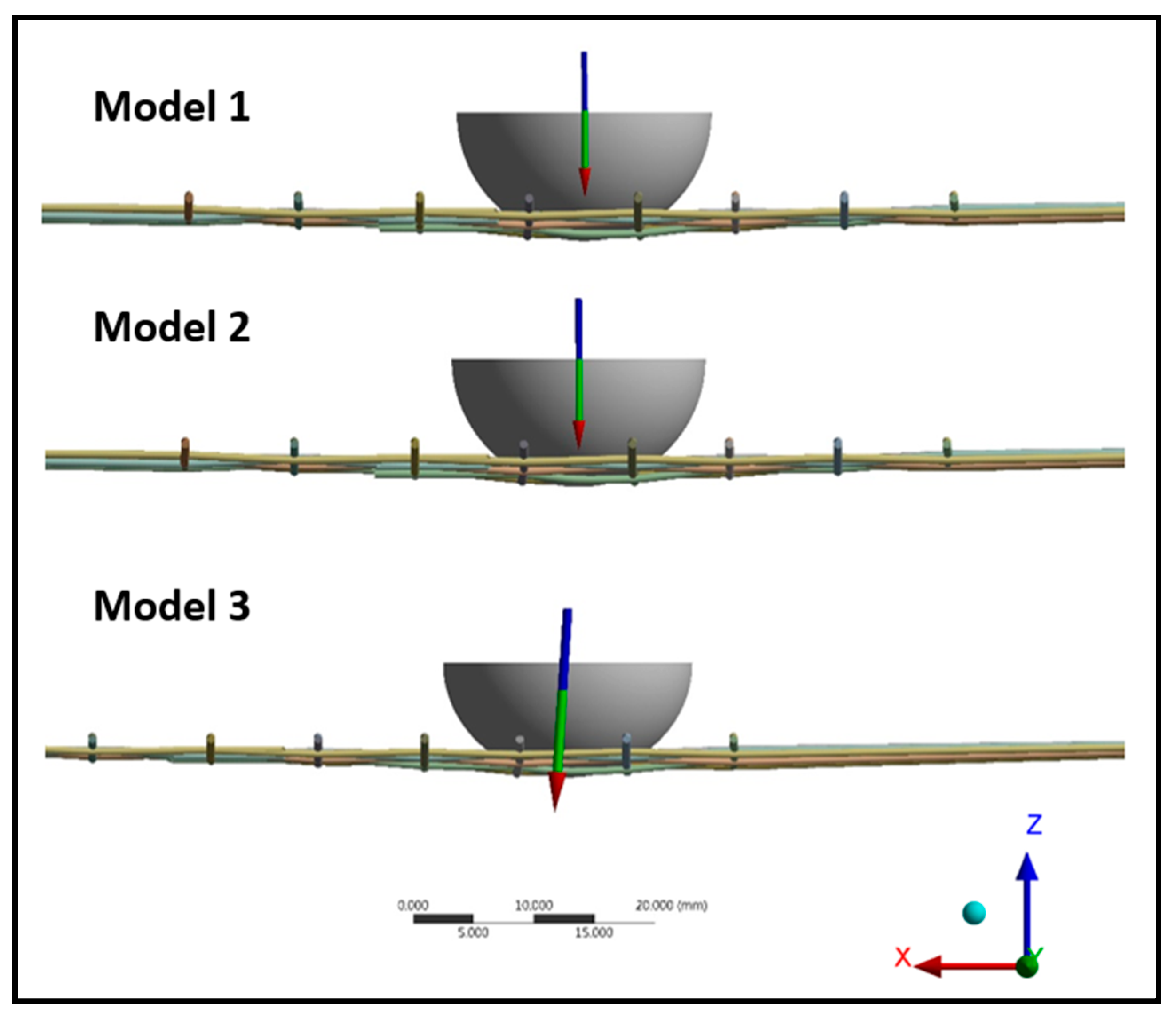
Three string tension-impact models were tested. Model 1 (Figure 2) assumed uniform string tension of 26 lbs (which is the amount commonly chosen by players) with ball impact in the middle. For model 2 and 3, the inner four strings (in both x and y directions) had the tension of 26 lbs but the outer strings had lower tension of 25 lbs. Impact occurred in the middle for model 2 (Figure 2), and between the 25 and 26 lbs strings in negative X direction for model 3 (Figure 2).

3. Results

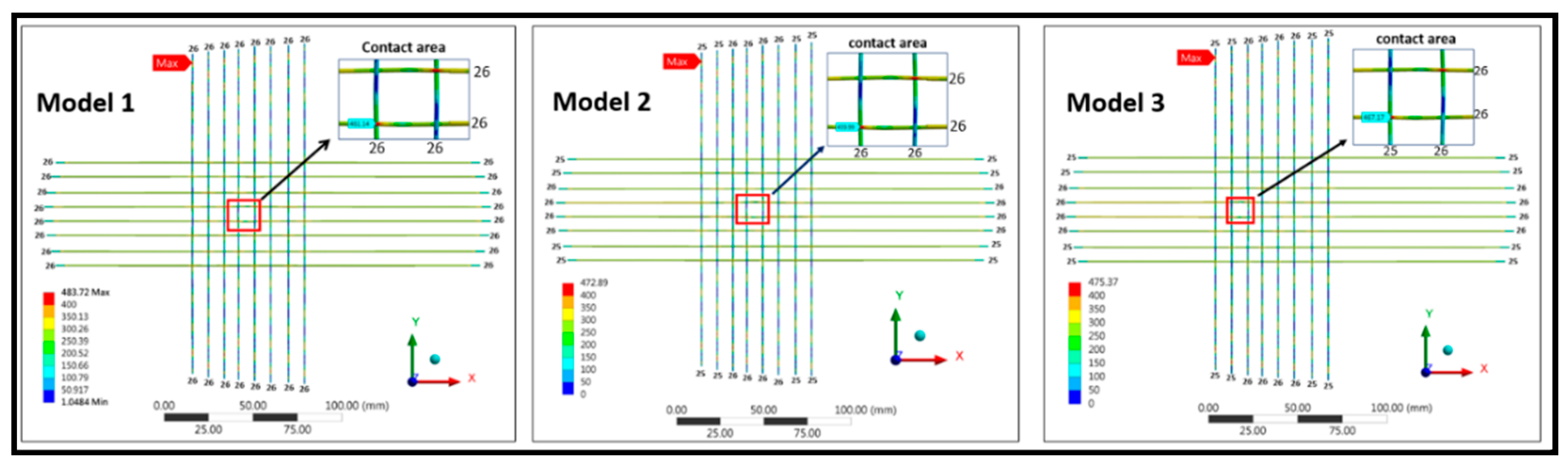
The simulation results revealed that the maximum von Mises stress of the strings occurred near the edge of the shortest medial-lateral string (Figure 3 and

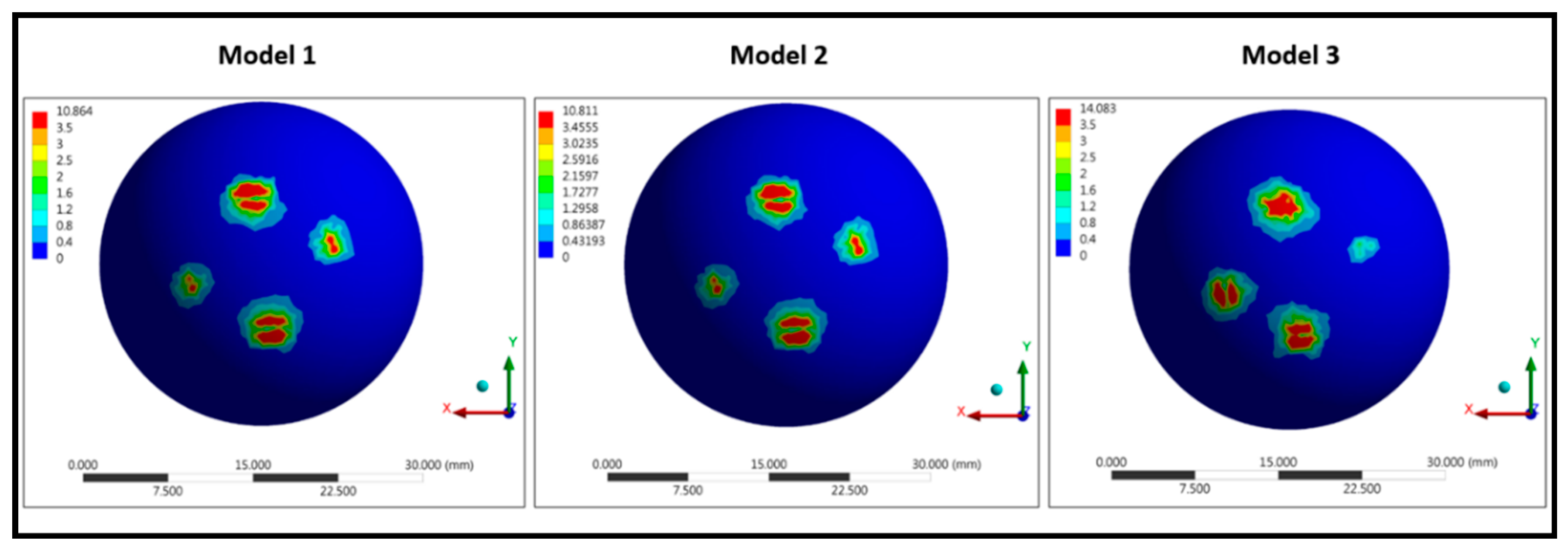
Table 1. Maximum von Mises stress (MPa).

	Model 1	Model 2	Model 3
String-bed	483.72	472.89	475.37
Contact area	461.14	459.99	467.17
Ball	10.86	10.81	14.08

). Maximum von Mises stress values for model 1, 2, and 3 were 483.72, 472.89, and 475.37 MPa, respectively. Maximum von Mises stress values at the contact region of the spring-bed/ball head for model 1, 2, and 3 were 461.14/10.86, and 459.99/10.81, and 467.17/14.08 MPa, respectively (Figure 3 and Figure 4 and Table 1). Although magnitudes of the forces between the string-bed and ball head (47.91, 47.29, and 47.77 N for model 1, 2, and 3, respectively) were comparable for the three models (Figure 5 and

Table 2. Force magnitude and components (N) for the three models.

	Model 1	Model 2	Model 3
Magnitude	47.91	47.29	47.77
X component	−0.27	−0.097	2.81
Y component	0.00987	0.63	−0.90
Z component	−47.91	−47.28	−47.68

), distinct features could be identified for each model. With nonuniform string tension, the same impact position resulted in a considerably greater magnitude of Y force component (and slightly less magnitude in the X direction) for model 2. Moving the impact position in the negative X direction (in model 3) resulted in a greater magnitude of force component in both X and Y directions (Table 2) and disparate von Mises stress distribution pattern on the ball (Figure 4).

4. Discussion

The present study investigated von Mises stress responses of badminton racket-shuttlecock impact with finite element modeling. The nonlinear behavior due to friction between strings increased difficulty in achieving numerical convergence upon string tension application. To have reasonable results without extensive computation effort, the present models included 16 intertwined strings around the sweet spot. With the same impact location (in the middle), slightly lowering the tension of outer strings (from 26 to 25 lbs) caused small changes in maximum von Mises stress on the string-bed and ball head. It is noteworthy that the off-centered impact (in the negative X direction) in model 3 resulted in a substantial increase in maximum von Mises stress on the string-bed and ball head, probably due both to nonuniform string tension and shortened string length toward the top of the racket. In addition, the direction of the ball-racket contact force was also changed by this off-centered impact due to the largely increased horizontal force component (especially in the X direction). This change in force direction would possibly cause greater difficulty in controlling the ball (shuttlecock) landing position, which might be the reason for players to use rackets with uniform string tension.

There are certain limitations to this study. To reduce computation effort, 16 perpendicularly intertwined strings were used in the simulation instead of modeling the whole string-bed. Neglecting part of the strings may lower the overall stiffness of the string-bed during ball impact, resulting in lower stress values in the current results.

5. Conclusions

The present study revealed the possibility of investigating badminton ball-racket impact responses with realistic finite element modeling. Slightly lowering the tension of off-centered strings had minimal effect on von Mises stress distribution of the ball and string-bed, but off-centered impact resulted in greater maximum von Mises stress values. The off-centered impact caused comparable contact force magnitude but altered force direction. Further investigation is needed for understanding the effect of varying string tension on sweet spot location and racket frame endurance.