Effectiveness of a Snowboarding Simulation Using the Distinct Element Method †
Abstract
:1. Introduction
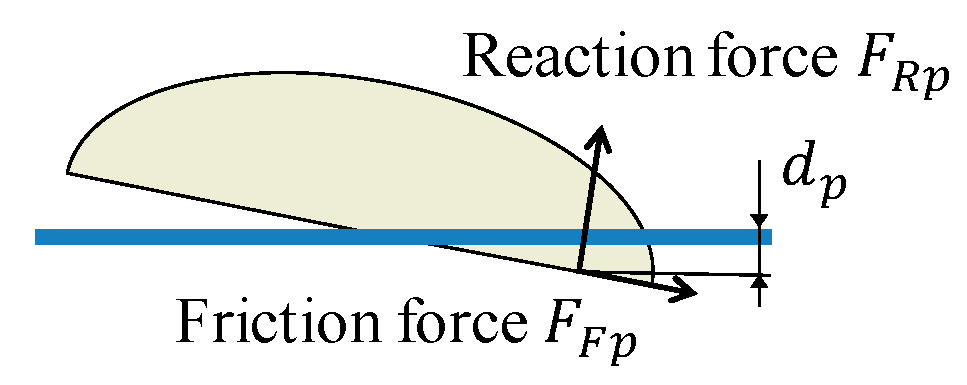
2. Mechanism of Snowboard Turn
3. Simulation Method
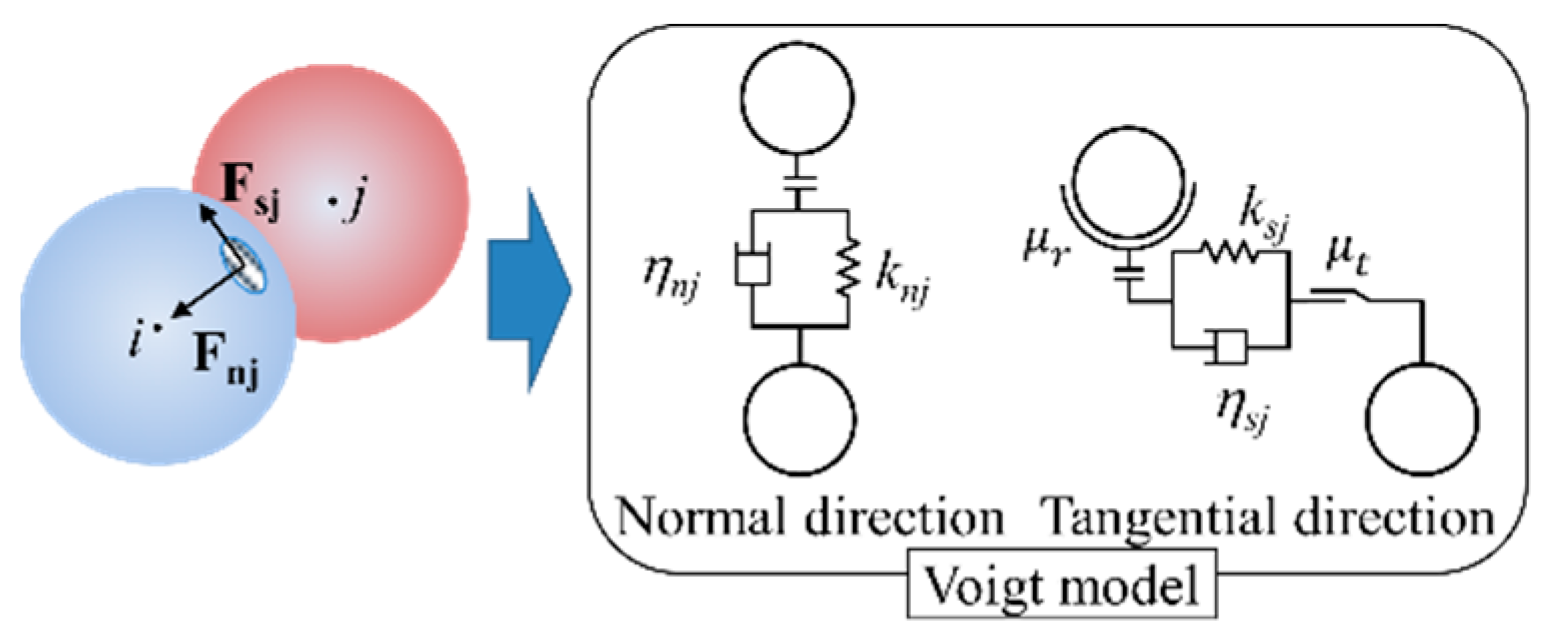
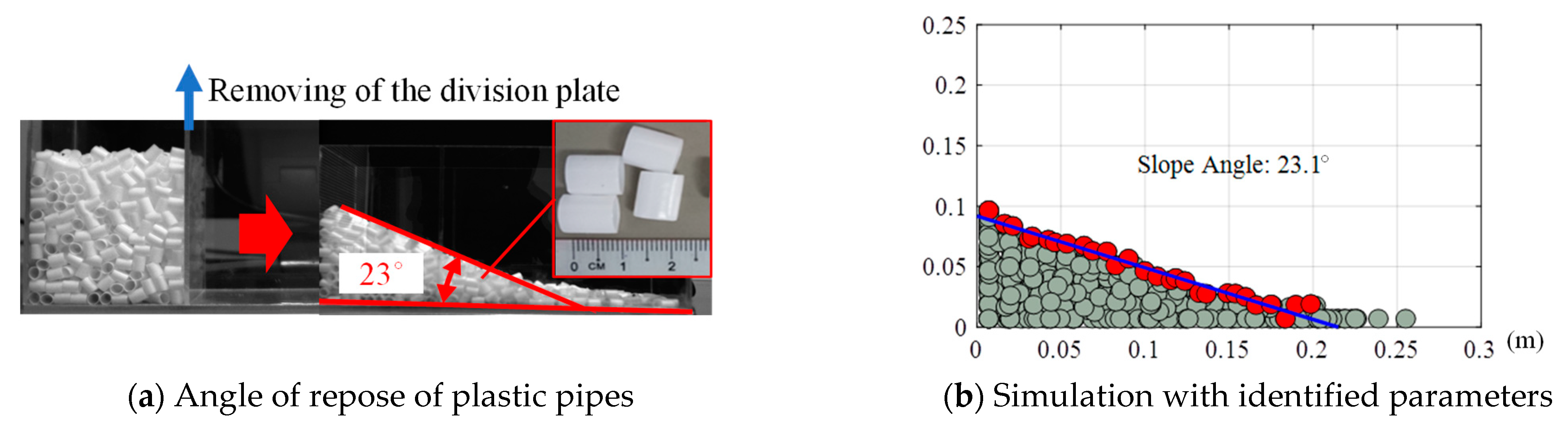
3.1. Snow Model in Distinct Element Method (DEM)
3.2. Conventional Snow Model (Linear Spring Model)
4. Test Equipment
5. Test and Simulation Conditions
6. Test Results and Simulation Results
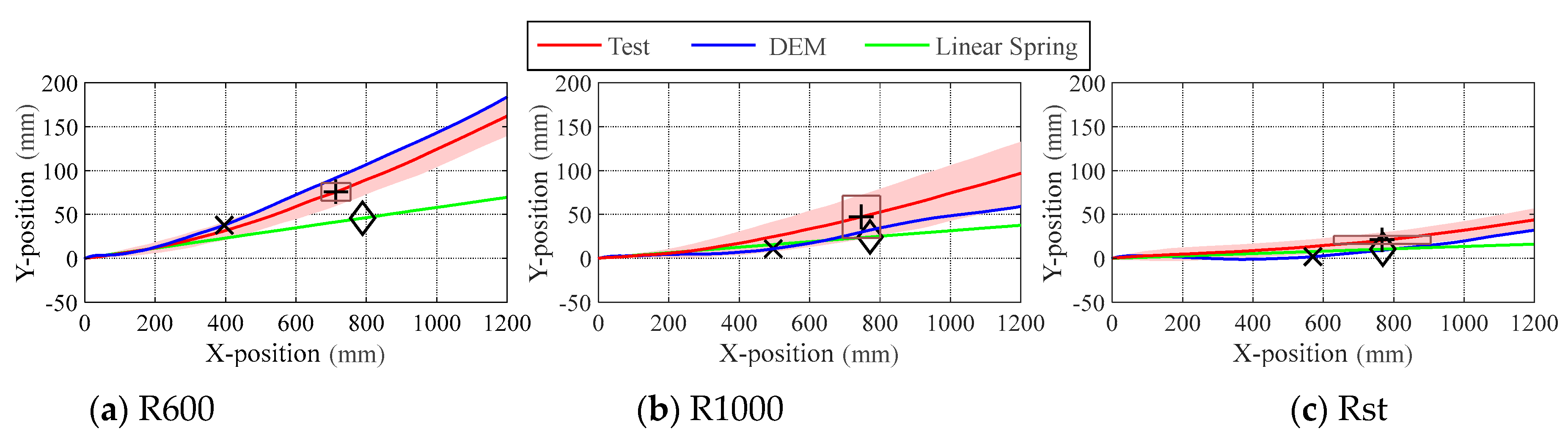
6.1. Trajectory
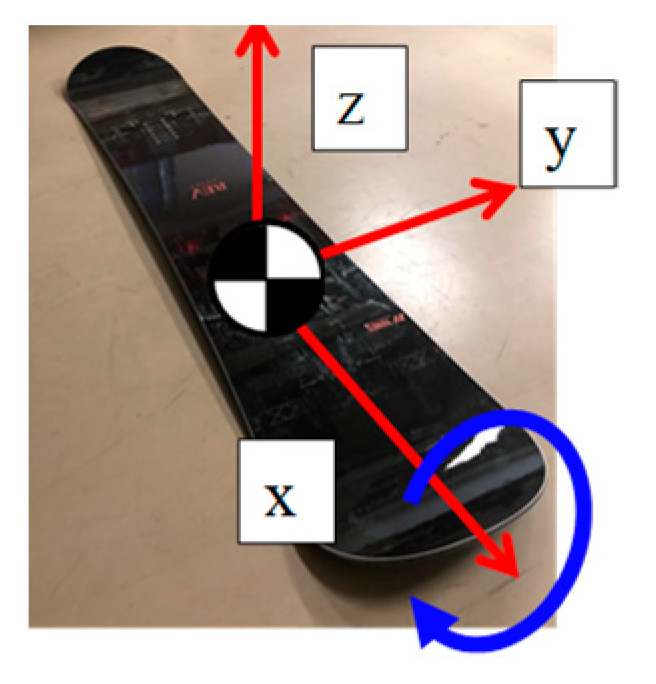
6.2. Board Postures
7. Conclusions
Acknowledgments
References
- Sakata, T.; Tsukiyama, M.; Hosokawa, K. Study on Simulation of Snowboard Turn. Mech. Eng. J. 1999, 65, 4431–4437. [Google Scholar] [CrossRef]
- Scott, N.; Yoneyama, T.; Kagawa, H.; Osada, K. Measurement of ski snow-pressure profiles. Sports Eng. 2007, 10, 145–156. [Google Scholar] [CrossRef]
- Petrone, N. The use of an Edge Load Profile static bench for the qualification of alpine skis. Procedia Eng. 2012, 34, 385–390. [Google Scholar] [CrossRef]
- Federolf, P.; JeanRichard, F.; Fauve, M.; Lüthi, A.; Rhyner, H.-U.; Dual, J. Deformation of snow during a carved ski turn. Cold Reg. Sci. Technol. 2006, 46, 69–77. [Google Scholar] [CrossRef]
- Mössner, M.; Heinrich, D.; Schindelwig, K.; Kaps, P.; Lugner, P.; Schmiedmayer, H.-B.; Schretter, H.; Nachbauer, W. Modeling of the Ski-Snow Contact for a Carved Turn. In The Engineering of Sport 6; Springer: New York, NY, USA, 2006; pp. 195–200. [Google Scholar]
- Abe, M.; Fujino, T.; Saito, F.; Takahata, K.; Iwamoto, K. Three-Dimensional Dynamic Simulation Analysis of Snow Removal Characteristics of Rotary Equipment. J. Syst. Des. Dyn. 2011, 5, 982–993. [Google Scholar] [CrossRef]
- Yoshida, T.; Hojo, A.; Kuratani, F. Simulation of snowboarding on snow surface modelled with particle elements. In Proceedings of the 6th International Congress on Sport Sciences Research and Technology Support, Seville, Spain, 20–21 September 2018; pp. 23–26. [Google Scholar]
- Fukumoto, Y.; Sakaguchi, H.; Murakami, A. The role of rolling friction in granular packing. Granul. Matter 2013, 15, 175–182. [Google Scholar] [CrossRef]





| Sidecut Radius | R600 | R1000 | Rst | ||
|---|---|---|---|---|---|
| Mass (g) | Weight | 154 | |||
| Board | 419 | 537 | 603 | ||
| Center of gravity (mm) | x | 0.2 | 0.2 | −1.1 | |
| y | 11 | 10 | 8.1 | ||
| z | 19 | 18 | 16 | ||
| Particle number | 22,821 | ||
| Radius r (mm) | 7 | ||
| Mass (g) | 0.11 | ||
| Friction coefficient | Board–Particle | 0.167 | |
| 0.122 | |||
| 0.12 | |||
| Spring constant | (N/mm) | 8.91 | |
| (N/mm) | 3.18 | ||
| 28.6 | |||
| Damping coefficient | (Ns/mm) | 1.90 × 10−3 | |
| (Ns/mm) | 1.14 × 10−3 | ||
| Spring constant K ((N/m)/m2) | 1.67 × 105 |
| 0.122 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yoshida, T.; Nakamura, S.; Kuratani, F. Effectiveness of a Snowboarding Simulation Using the Distinct Element Method. Proceedings 2020, 49, 101. https://doi.org/10.3390/proceedings2020049101
Yoshida T, Nakamura S, Kuratani F. Effectiveness of a Snowboarding Simulation Using the Distinct Element Method. Proceedings. 2020; 49(1):101. https://doi.org/10.3390/proceedings2020049101
Chicago/Turabian StyleYoshida, Tatsuya, Shogo Nakamura, and Fumiyasu Kuratani. 2020. "Effectiveness of a Snowboarding Simulation Using the Distinct Element Method" Proceedings 49, no. 1: 101. https://doi.org/10.3390/proceedings2020049101
APA StyleYoshida, T., Nakamura, S., & Kuratani, F. (2020). Effectiveness of a Snowboarding Simulation Using the Distinct Element Method. Proceedings, 49(1), 101. https://doi.org/10.3390/proceedings2020049101




