Abstract
In this paper, we present the results of a numerical simulation of thermodynamics for the array of Classical Heisenberg spins placed on a 2D square lattice, which effectively represents the behaviour of a single layer. Using the Metropolis algorithm, we show the temperature behaviour of the system with a competing Heisenberg and Dzyaloshinskii–Moriya interaction (DMI) in contrast with the classical Heisenberg system. We show the process of nucleation of the skyrmion depending on the value of the external magnetic field. We proposed the controlling method for the movement of skyrmions.
Keywords:
Monte Carlo method; magnetic skyrmion; Heisenberg model; Dzyaloshinskii–Moriya interaction PACS:
05.10.Ln; 75.10.Hk; 75.70.Cn
1. Introduction
Spintronics or magnetic electronics is continually evolving, and new promising materials for new storage and processing data devices are emerging. Racetrack memory (RM) is considered as one of the most attractive non-volatile data storages in future advanced computer architectures. The existing RM samples are based on the motion of the domain wall (DW), which, however, has some internal limitations, such as scalability, density, and energy consumption due to the physical properties inherent in the DW. Recently, magnetic skyrmions have been proposed as an alternative to DW in racetrack memory. The skyrmion’s characteristics, such as the nanoscale size, topological stability, and an ultra-low current (depinning current) make it a promising element of data storage in future electronics with an extremely low power consumption, high-speed read-write, and ultra-high recording density. A magnetic skyrmion is a topological object consisting of a skyrmion core, an outer domain, and a wall that separates the skyrmion core from the outer domain. The skyrmion size and wall width are two fundamental quantities of a skyrmion that depend primarily on material parameters, such as exchange energy, magnetic anisotropy, the Dzyaloshinskii–Moriya interaction, and magnetic field [1,2,3,4,5]. At the moment, theoretical and numerical studies are primarily being carried out, and experimental approaches to the construction of magnetic running memory based on skyrmions are being developed. The superiority of such technology over racetrack memory based on the motion of the domain wall has already been demonstrated [6,7].
2. Models and Methods
The Heisenberg model is one of the models used in statistical physics to model ferromagnetism. It is used in the study of critical points and phase transitions of different magnetic systems. We used the lattice Hamiltonian, consisting of the Heisenberg exchange and DMI interaction terms for the microscopic description of a chiral helimagnet [8,9], see Formulas (1)–(3).
where is the atomic spin, J is the ferromagnetic short-range exchange interaction, and the DMI interaction [8,9].
The Formulas (2) and (3) were used for calculating the interaction between and its neighbours along the X axis and Y axis for the 2D lattice. When calculating the total energy of the system, only unique neighbours standing “above” along the Y axis and “right” along the X axis were taken into account for a pairs interaction.
A spin was introduced as a three-dimensional unit-length vector in accordance with formulas:
where .
In the frame of our computer model, the magnetic film had a size of . The magnetic film representing the system of Heisenberg spins was placed in the nodes of a 2D square lattice, where a spin had four nearest neighbours in the film (with periodic boundary conditional).
For the computer simulation, we used parallel modification of the Metropolis algorithm [10,11].
3. Results and Discussion
Below, we show the step-by-step process of nucleation of the skyrmion and skyrmion lattice by using the Metropolis algorithm. It is dependent on the value of the external out-of-plane magnetic field. The parameters of simulation were , and the size of the system was . Visualisation was made in Paraview [12].
In Figure 1, we have the stripe structure, because of the competition of the direct Heisenberg exchange and DM interaction. However, we had more than one spin in one stripe, which was the result of the impact of direct interaction. The external magnetic field was zero.
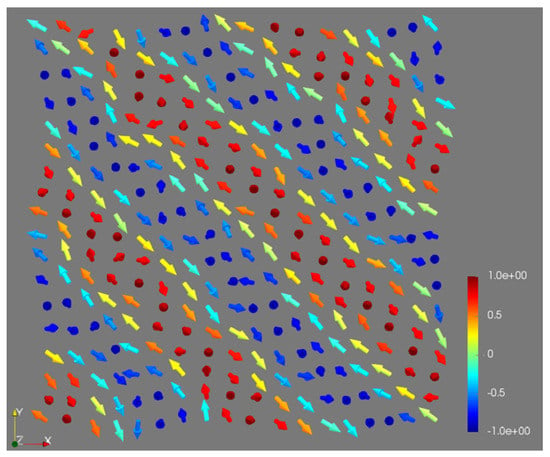
Figure 1.
A ground state of the system with DMI and the Heisenberg exchange—a Spiral state.
When we added a small external magnetic field, , we had the beginning of the process of nucleation of the skyrmion. Under the influence of an external magnetic field, a skyrmion was being formed in strips, and in general, we could see it changing in a distribution of a magnetic spin configuration. Finally, when we applied , we had skyrmion’s lattice in Figure 2.
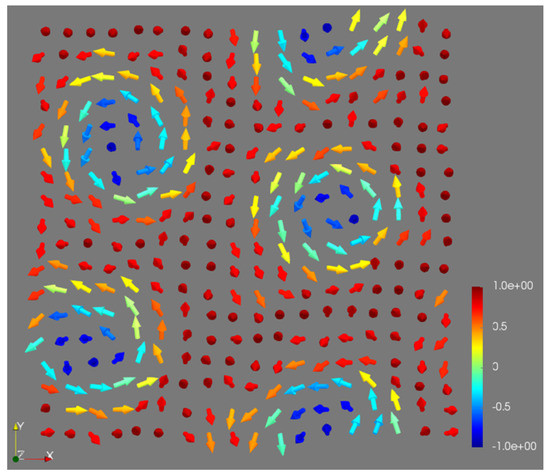
Figure 2.
Skyrmion’s lattice.
For solving the problem with a random point for nucleation of the skyrmion, we applied an in-plane magnetic field to a small area of the sample to create the skyrmion at a specific point.
We could also “push” the skyrmion from one side to another using this in-plane magnetic field. This is a rather precise method—see Figure 3. The main problem is that it is really difficult to reproduce this in a physical experiment, but our colleagues are working with this experimental realisation. Now, we are working under another method, using control of the anisotropy by applying a voltage to a sample.

Figure 3.
Movement of the skyrmion.
4. Conclusions
In the frame of the classical Heisenberg model, lattice spin systems with direct short- and Dzyaloshinskii–Moriya interactions were investigated by using Monte Carlo methods.
The energy of direct interaction, which contributes to the collinear alignment of neighbouring spins and controls the ordering in the system, is given by the Heisenberg exchange integral. A much weaker interaction, favouring the perpendicular orientation of neighbouring spins, exists in some Heisenberg magnets, in which electrons have a strong spin-orbit coupling. The energy of this interaction is described by the DMI interaction and leads to the fact that the spins deviate from the parallel orientation. As a result, there is a competition between collinear and non-collinear alignments of spins.
In this paper, we proposed a method for manipulation of the position of a skyrmion using an in-plane magnetic field.
Author Contributions
V.K., concept and model, A.P. and E.V., software and visualization. All authors have read and agreed to the published version of the manuscript.
Funding
The research was carried out within the state assignment of FASO of Russia No. 075-00400-19-01.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bogdanov, A.; Hubert, A. Thermodynamically stable magnetic vortex states in magnetic crystals. J. Magn. Magn. Mater. 1994, 138, 255–269. [Google Scholar] [CrossRef]
- Dzyaloshinsky, I. A thermodynamic theory of “weak” ferromagnetism of antiferromagnetics. J. Phys. Chem. Solids 1958, 4, 241–255. [Google Scholar] [CrossRef]
- Moriya, T. Anisotropic superexchange interaction and weak ferromagnetism. Phys. Rev. 1960, 120, 91. [Google Scholar] [CrossRef]
- Kapitan, V.Y.; Shevchenko, Y.A.; Perzhu, A.V.; Vasiliev, E.V. Thermodynamic Properties of Heisenberg Spin Systems. Key Eng. Mater. 2019, 806, 142–154. [Google Scholar] [CrossRef]
- Wang, X.; Yuan, H.; Wang, X. A theory on skyrmion size. Commun. Phys. 2018, 1, 31. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, Y.; Ezawa, M.; Zhao, G.; Zhao, W. Magnetic skyrmion transistor: Skyrmion motion in a voltage-gated nanotrack. Sci. Rep. 2015, 5, 11369. [Google Scholar] [CrossRef] [PubMed]
- Kang, W.; Zheng, C.; Huang, Y.; Zhang, X.; Lv, W.; Zhou, Y.; Zhao, W. Compact modeling and evaluation of magnetic skyrmion-based racetrack memory. IEEE Trans. Electron Devices 2017, 64, 1060–1068. [Google Scholar] [CrossRef]
- Do Yi, S.; Onoda, S.; Nagaosa, N.; Han, J.H. Skyrmions and anomalous Hall effect in a Dzyaloshinskii–Moriya spiral magnet. Phys. Rev. B 2009, 80, 054416. [Google Scholar]
- Belemuk, A.; Stishov, S. Phase transitions in chiral magnets from Monte Carlo simulations. Phys. Rev. B 2017, 95, 224433. [Google Scholar] [CrossRef]
- Kapitan, V.Y.; Nefedev, K. Labyrinth domain structure in the models with long-range interaction. J. Nano- Electron. Phys. 2014, 6, 03005. [Google Scholar]
- Andriushchenko, P.D.; Peretyatko, A.A.; Kapitan, V.Y.; Perzhu, A.V.; Nefedev, K.V. Interplay of frustrations, interaction length, and dilution on magnetic transitions in vector models. J. Phys. 2017, 936, 012081. [Google Scholar] [CrossRef]
- Ahrens, J.; Geveci, B.; Law, C. Paraview: An end-user tool for large data visualization. In The Visualization Handbook; Los Alamos National Laboratory: Los Alamos, NM, USA, 2005; Volume 717. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).