Fast Tuning of Topic Models: An Application of Rényi Entropy and Renormalization Theory ^†

Abstract

In practice, the critical step in building machine learning models of big data (BD) is costly in terms of time and the computing resources procedure of parameter tuning with a grid search. Due to the size, BD are comparable to mesoscopic physical systems. Hence, methods of statistical physics could be applied to BD. The paper shows that topic modeling demonstrates self-similar behavior under the condition of a varying number of clusters. Such behavior allows using a renormalization technique. The combination of a renormalization procedure with the Rényi entropy approach allows for fast searching of the optimal number of clusters. In this paper, the renormalization procedure is developed for the Latent Dirichlet Allocation (LDA) model with a variational Expectation-Maximization algorithm. The experiments were conducted on two document collections with a known number of clusters in two languages. The paper presents results for three versions of the renormalization procedure: (1) a renormalization with the random merging of clusters, (2) a renormalization based on minimal values of Kullback–Leibler divergence and (3) a renormalization with merging clusters with minimal values of Rényi entropy. The paper shows that the renormalization procedure allows finding the optimal number of topics 26 times faster than grid search without significant loss of quality.

1. Introduction

Machine learning algorithms (ML) are increasingly adopted to solve numerous problems arising from the abundance of data in a growing number of research fields. However successful they are, these solutions are too often expensive in terms of time and computing resources. Here, one bottleneck is the problem of hyperparameter optimization, traditionally approached with the so-called grid search strategy, which is an exhaustive search for optimal values in a manually defined subspace. One possible way to overcome this limitation, at least for some models, could be found in ideas from statistical physics.

Among ML models, topic modeling (TM) has a special place. Due to its power to reduce the dimensionality of large text data and ease of integrating into numerous types of research design, TM has become a highly valuable technique for social sciences [1]. However, TM requires to specify the number of topics manually, which is problematic as it is unknown for most data. Available approaches to the problem of finding the optimal number of topics are built on the grid search strategy [2,3]. One alternative approach is to look for the minimum of Rényi entropy [4]. Moreover, it is possible to speed up the entropy approach by incorporating the renormalization procedure, exploiting the fact that the mathematical formalism of Rényi entropy is closely related to the fractal approach where the deformation parameter q plays the scaling role [5].

Basics of Topic Modeling

Topic modeling is based on the assumption that a document collection has a finite set of word distributions. Each such word distribution could be called a ‘topic’ or a thematical cluster. In such a model, every word has a varying probability of appearing in each cluster; it is a so-called fuzzy algorithm of bi-clustering where words and documents are simultaneously assigned to topics (clusters). Here, the probability of encountering a word w in a given document d is expressed as follows [6]:

$$p\left(w\right|d)=\sum _{t\in T}p\left(w\right|t)p\left(t\right|d)=\sum _{t\in T}{\varphi }_{wt}{\theta }_{td},$$

(1)

where t is a topic, $p\left(w\right|t)$ is the distribution of words by topics and $p\left(t\right|d)$ is the distribution of topics by documents. Building a topic model involves finding a set of one-dimensional conditional distributions $p\left(w\right|t)\equiv \varphi (w,t)$, which constitute matrix $\mathsf{\Phi }$ (the distribution of words by topics), and $p\left(t\right|d)\equiv \theta (t,d)$ which form matrix $\mathsf{\Theta }$ (the distribution of documents by topics). Each of these distributions is latent as the probabilities of words in these distributions are unknown. In this paper, we consider the Blei model [7], where the distribution of topics by documents is assumed to be Dirichlet distribution with parameter $\alpha$.

2. Methods

2.1. Entropic Approach for Determining the Optimal Number of Topics

The entropy approach to TM tuning is based primarily on computing Rényi entropy for each topic solution while varying the number of topics and hyperparameters [4,8]. For TM, the Rényi entropy is expressed as follows:

$$S_q^R=\frac{ln\left(Z_q\right)}{q-1}=\frac{qln\left(q\tilde{P}\right)+q^{-1}ln\left(\tilde{\rho }\right)}{q-1}$$

(2)

where in $q=1/T$, T is the number of clusters or topics, $\tilde{\rho }=\frac{N}{WT}$ is the density-of-states function, W is the number of unique words in the dataset, N is the number of words with high probability (i.e., with ${\varphi }_{wt}>1/W$), $\tilde{P}=\frac{1}{T}{\sum }_{w,t}{\varphi }_{wt}·{𝟙}_{({\varphi }_{wt}-1/W)}$ is the sum of probabilities of all words with high probability, ${𝟙}_{(x-y)}=1$ if $x\ge y$ and ${𝟙}_{(x-y)}=0$ if $x<y$. Thus, $E=-Tln\left(\tilde{P}\right)$ is the energy of a topic model, $ln\left(\tilde{\rho }\right)$ is the Gibbs–Shannon entropy, $Z_q=e^{-qE+S}=\tilde{\rho }{\left(\tilde{P}\right)}^q$ is the partition function of a topic solution.

Rényi entropy has at least two benefits for topic modeling. (1) Rényi entropy allows measuring the degree of non-equilibrium in a topic model with varying number of topics and hyperparameters. (2) Rényi entropy captures two divergent processes; on the one hand, the increase of the number of topics leads to the dropping of the Gibbs–Shannon entropy, and, on the other, it leads to an increase of internal energy. The difference between these two processes has an area of equilibrium where they counterbalance each other. In this area, $S_q^R$ reaches its minimum. It has been shown that the minimum Rényi entropy corresponds to the number of topics identified by human coders [8]. Hence, the search for the $S_q^R$ minimum could, at least partly, substitute the manual labor of marking up document collections, substantially simplifying TM tuning on uncoded datasets.

The fractal-like behavior of TM has been shown in [9], demonstrating the existence of areas where the logarithm of the density-of-states function $\tilde{\rho }\left(ϵ\right)$ ($ϵ=\frac{1}{WT}$) changes linearly. At the same time, the transition between these areas corresponds to the regions of minimum Massieu function and, consequently, to the Rényi entropy minimum. Thus, the problem of finding the optimal number of topics (clusters) in TM could be reduced to locating the area that separates regions of self-similarity.

From the formal point of view, Rényi entropy of the statistical ensemble describes a multifractal structure that exhibits a renormalization effect related to the deformation parameter q [5]. Based on this property, it is possible to hypothesize that Rényi entropy being a deformed logarithm and following the logarithm of the density-of-states function can have renormalization properties. It is, thus, possible to examine the renormalization procedure of a single topical solution with a high enough number of topics.

2.2. General Formulation of the Renormalization Approach in Topic Modeling

In general, the renormalization procedure is a consequent coarsening of a single topic solution while varying the number of topics and computing Rényi entropy at each step of the procedure. The coarsening procedure involves merging of topic couples (columns in $\mathsf{\Phi }$ matrix) into a single topic (one column). After merging, the resulting topic is scaled as the sum of all word probabilities (in a topic) must be equal to 1 regardless of the total number of topics. Because the computation of the $\mathsf{\Phi }$ matrix depends on the used algorithm, the mathematical formulation of the renormalization procedure is algorithm-specific. Moreover, the results of merging depend on what particular topics are merged.

This paper investigates three criteria of merging. (1) Merging of similar topics, where the similarity is estimated with symmetric Kullback–Leibler (Jensen–Shannon) divergence, and the topic pair is chosen based on the minimal value computed pairwisely. (2) Merging based on the minimum of Rényi entropy, where the topics with local minima values are summed together. Here, local Rényi entropy is computed for a single topic. (3) Merging randomly selected columns.

2.3. Renormalization of Topic Models with Variational Inference

Let us consider the LDA model with a variational E-M algorithm [7]. Let T be a given number, which is set by the user. This model assumes that distribution over topics (topic proportions or topic weights) is the Dirichlet distribution with parameter $\alpha$. The output of this model is a vector $\alpha$ with T components and a matrix containing a distribution of words by topics: $\mathsf{\Phi }={\left({\varphi }_{wt}\right)}_{w\in W,t\in T}$, W is the number of rows (number of unique words), T is the number of columns (number of topics). Calculation of matrix $\mathsf{\Phi }$ is based on the variational expectation-maximization (E-M) algorithm, while for estimation of vector $\alpha$, the Newton–Rapson method is used. A key formula of this algorithm is the following [7]:

$${\mu }_{wt}={\varphi }_{wt}exp\left(\psi \left({\alpha }_t+\frac{L}{T}\right)\right),$$

(3)

where L is a document length, w is the current word, $\psi$ is digamma function, ${\mu }_{wt}$ is an auxiliary variable, which is used for updating ${\varphi }_{wt}$ during the variational E-M algorithm. We use an analog of Equation (3) for the task of renormalization. Thus, the renormalization algorithm consists of the following steps:

• We choose a pair of topics for merging according to one of the three possible criteria described in Section 2.2. Let us denote the chosen topics by $t_1$ and $t_2$.
• We merge the chosen topics. The word distribution of a ‘new’ topic resulted from merging of $t_1$ and $t_2$ is stored in column ${\varphi }_{·t_1}$ of matrix $\mathsf{\Phi }$:

  $${\varphi }_{w{t}_1}:={\varphi }_{w{t}_1}exp\left(\psi \left({\alpha }_{t_1}\right)\right)+{\varphi }_{w{t}_2}exp\left(\psi \left({\alpha }_{t_2}\right)\right),$$

  (4)

  where $\psi$ is a digamma function. Then, we normalize the obtained column ${\varphi }_{·t_1}$ so that ${\sum }_{w\in W}{\varphi }_{w{t}_1}=1$. We also recalculate ${\alpha }_{t_1}:={\alpha }_{t_1}+{\alpha }_{t_2}$, which corresponds to the hyper-parameter of the ‘new’ topic. Then, we delete column ${\varphi }_{·t_2}$ from matrix $\mathsf{\Phi }$ and element ${\alpha }_{t_2}$ from vector $\alpha$. Let us note that this step leads to a decrease in the number of topics by one, i.e., we have $T-1$ topics at the end of this step. Further, vector $\alpha$ is normalized so that ${\sum }_t{\alpha }_t=1$.
• We calculate the overall value of the global Rényi entropy. Since a new topic solution (matrix $\mathsf{\Phi }$) is formed in the previous step, we recalculate the global Rényi entropy for this solution. We refer to entropy calculated according to Equation (2) as global Rényi entropy since it accounts for distributions of all topics.

Steps 1–3 are repeated until only two topics remain. Then, based on the results of renormalization, a curve of the global Rényi entropy as a function of the number of topics is drawn.

In order to determine the quality of the renormalization procedure, one needs to compare the Rényi entropy curve, which is obtained through the renormalization and Rényi entropy curve, which is obtained through successive calculations of topic models with a varying number of topics. Below, we demonstrate and discuss the results of computer experiments on renormalization.

3. Results

3.1. Description of Datasets and Experiments

For experiments two datasets were employed:

• Dataset in Russian (Lenta.ru). This dataset contains news articles in the Russian language where each news item was manually assigned to one of ten topic classes by the dataset provider [10]. However, as some of these topics could be considered folded or correlated (i.e., topic ‘soccer’ is a part of topic ‘sports’), this dataset could be represented by 7–10 topics. We considered a class-balanced subset of this dataset, which consisted of 8624 news texts (containing 23,297 unique words).
• Dataset in English (20 Newsgroups dataset [11]). This well-known dataset contains articles assigned by users to one of 20 newsgroups. Since some of these topics can be unified, this document collection can be represented by 14–20 topics [12]. The dataset is composed of 15,404 documents with 50,948 unique words.

For each dataset, we performed topic modeling (LDA with variational E-M algorithm) in the range of 2–100 topics in the increments of one topic. Then, topic solutions on 100 topics undergone renormalization. Based on the results of the renormalization, curves of Rényi entropy as a function of the number of topics were plotted. Finally, the obtained curves were compared to Rényi entropy curves obtained using successive topic modeling.

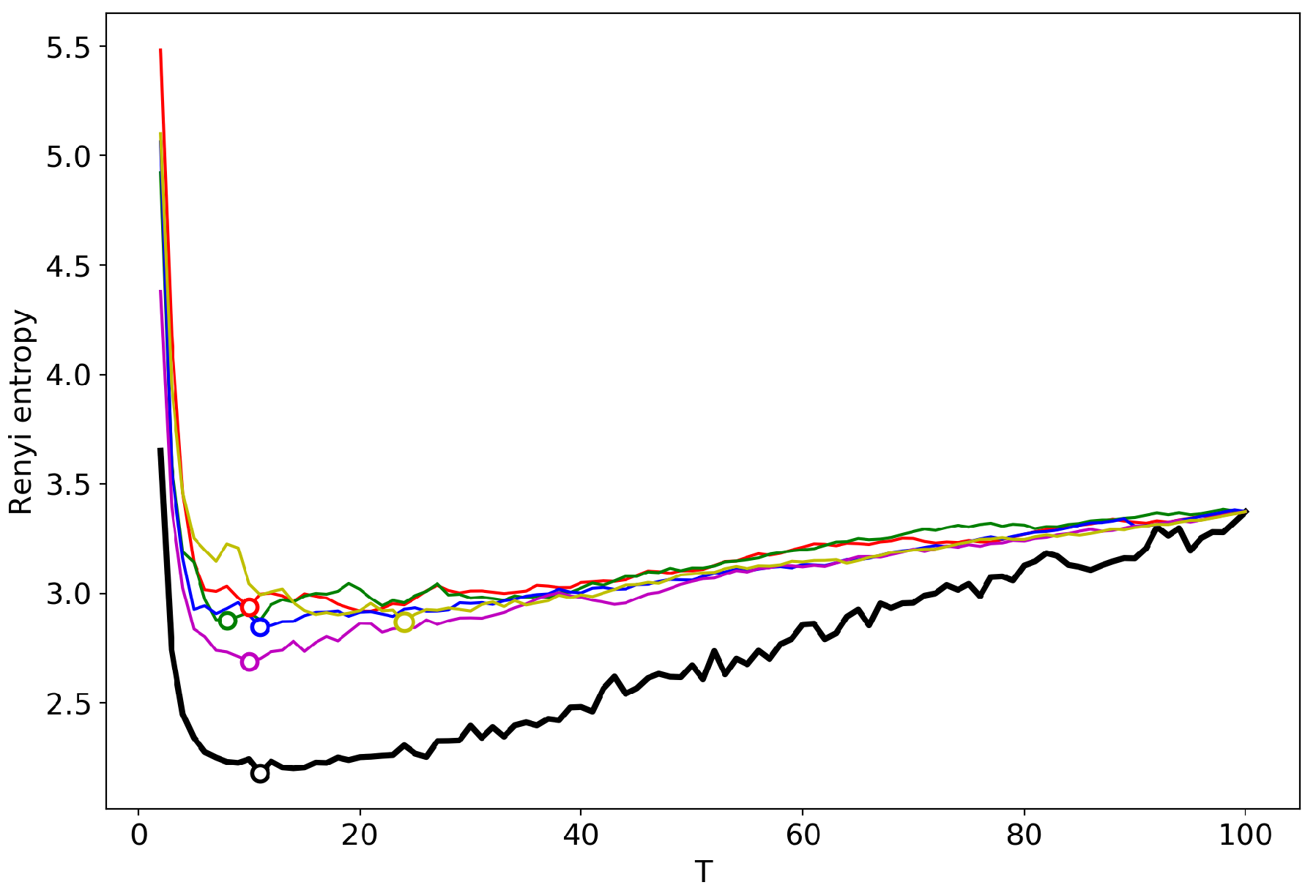
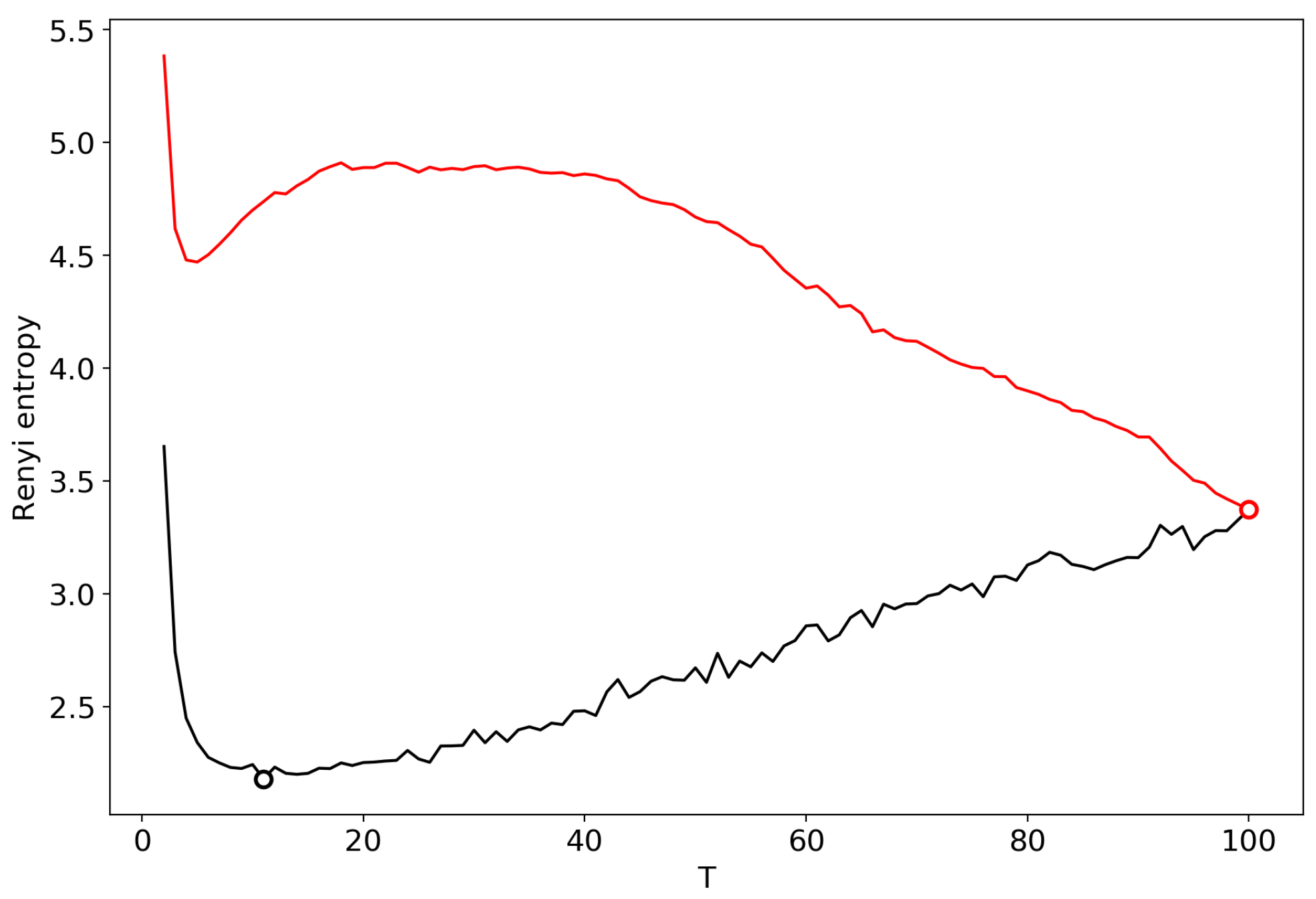
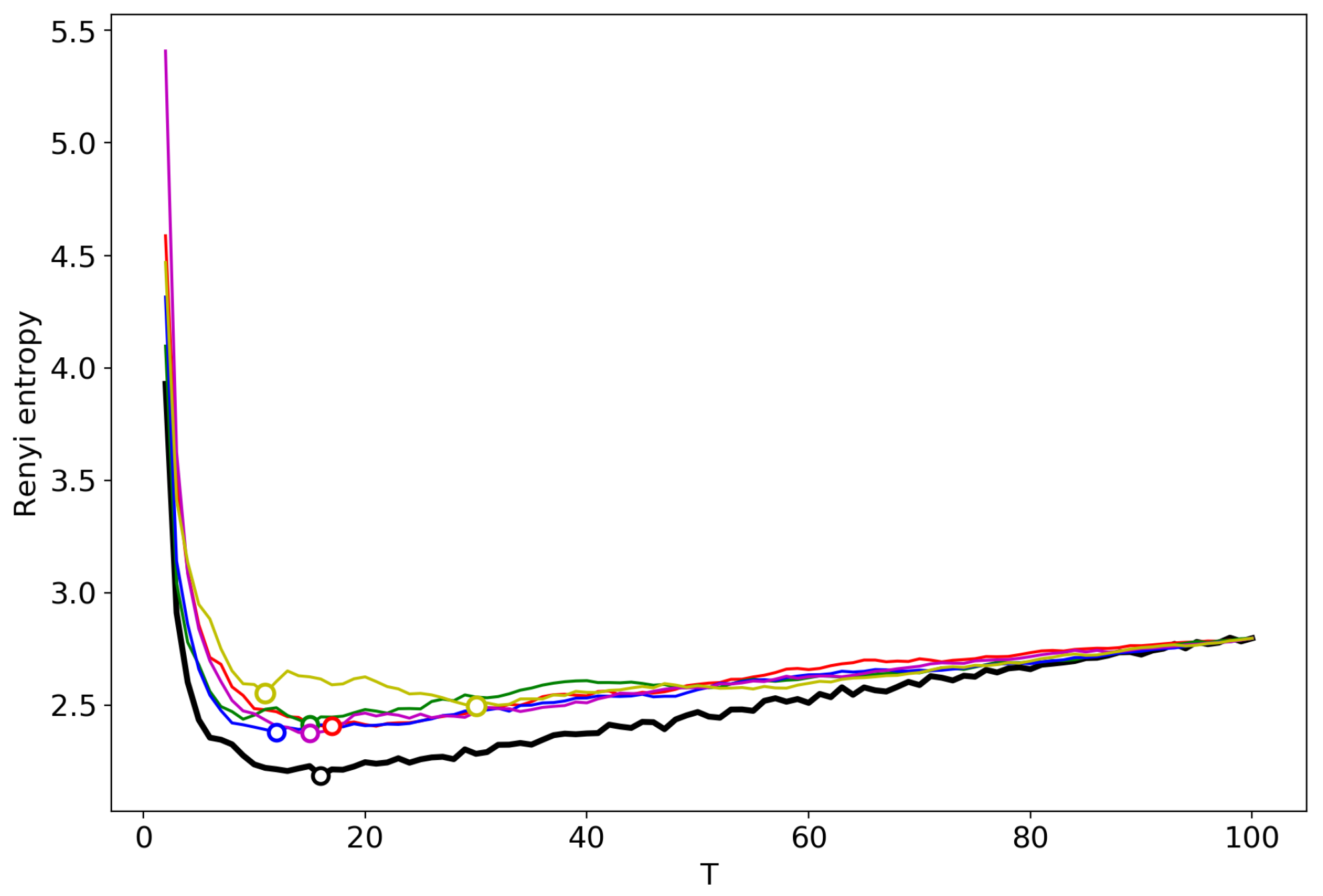
3.2. Results for the Dataset in Russian

Figure 1 demonstrates the Rényi entropy curve obtained by successive topic modeling with varying number of topics (black line) and Rényi entropy curves obtained by renormalization with merging of randomly chosen topics. Here and further, minima are denoted by circles in the figures. The minimum of original Rényi entropy (black line) corresponds to 11 topics for the dataset in Russian. The minima of ‘renormalized’ Rényi entropy fluctuate in the range of 8–24 topics. However, after averaging over five runs of renormalization, the minimum corresponds to 12–13 topics, which is very close to the result obtained by successive calculation of topic models. Even though, on average, renormalized Rényi entropy has larger values than that without renormalization, the overall behavior is similar.

Figure 2 demonstrates the renormalized Rényi entropy curve where topics for merging are selected according to minimum local Rényi entropy calculated for separate topics. The renormalized curve reaches its minimum on ten topics, which is very close to the result obtained without renormalization and matches the original human markup.

Figure 3 shows a renormalized Rényi entropy curve, where topics for merging are selected according to minimum Kullback–Leibler (KL) divergence between each topic pairs. Figure 3 displays significant distortion of the Rényi entropy curve obtained using renormalization. Thus, we conclude that renormalization based on minimum KL divergence does not apply to the task of searching for the optimal number of topics.

3.3. Results for the Dataset in English

Figure 4 demonstrates the renormalized Rényi entropy curves with randomly chosen topics for merging.

The minimum points of renormalized Rényi entropy for five runs lie in the range of 11–17 topics. Averaging over five runs of renormalization, we obtain that minimum corresponds to 14 topics. The minimum of Rényi entropy obtained by successive topic modeling with varying number of topics (black line) corresponds to 16 topics.

Figure 5 demonstrates the renormalized Rényi entropy curve where topics for merging are selected according to the minimum local Rényi entropy calculated for separate topics. The minimum of the renormalized curve corresponds to 17 topics. Thus, a renormalization of topic models based on merging of topics with minimal values of local entropy leads to the result, which is almost identical to that obtained with the successive calculation of topics models (i.e., without renormalization).

Figure 6 shows renormalized Rényi entropy, where the topics for merging are selected according to minimum KL divergence. This figure demonstrates that such type of renormalization does not allow us to determine the optimal number of topics since there is no definite minimum of Rényi entropy. Therefore, we recommend applying renormalization with the random merging of topics or with minimum local Rényi entropy.

3.4. Computational Speed

Table 1. Computational speed.

Dataset	Successive TM Simulations	Renormalization (Random)	Renormalization (Minimum Rényi Entropy)	Renormalization (Minimum KL Divergence)
Russian dataset	780 min	1 min	1 min	4 min
English dataset	1320 min	3 min	3 min	10 min

demonstrates time costs of Rényi entropy calculations for $T=[2,100]$ according to different methods. The first column corresponds to successive runs of topic modeling for $T=[2,100]$ in the increments of one topic. The second, the third and the fourth columns demonstrate time costs of renormalization of a single topic solution on 100 topics with random merging of topics, with merging of topics with minimum local Rényi entropy and with merging of topics with minimum KL divergence, where calculation of a single topic solution on 100 topics takes 26 min for the dataset in Russian and 40 min for the dataset in English. One can see that renormalization provides a significant gain in time that is essential when dealing with big data.

4. Discussion

In this work, we propose a renormalization approach to the LDA topic model with variational inference. Our approach allows us to efficiently determine the location of minimum Rényi entropy without a computationally intensive grid search technique. We demonstrate that renormalization based on merging of topics with minimum local Rényi entropy provides the best result in terms of accuracy and computational speed simultaneously. It was shown that for this type of renormalization, the global minimum point of Rényi entropy is almost equal (with an accuracy of $\pm 1$ topic) to the minimum point of Rényi entropy calculated according to successive topic modeling. Renormalization with the merging of random topics also leads to satisfactory results; however, it requires multiple runs and subsequent averaging over all runs. Let us note that renormalization is applicable to datasets in different languages and with a different number of topics in the collections. Application of renormalization allows us to speed up the searching of the optimal number of topics by at least 26 times. The proposed renormalization approach could be adapted for topic models with a sampling procedure. Furthermore, our renormalization approach can be adapted for simultaneous estimation of the number of topics and fast tuning of other hyper-parameters of topic models, including regularization parameters.