The New Method Using Shannon Entropy to Decide the Power Exponents on JMAK Equation  ^†

Abstract

The JMAK (Johnson–Mehl–Avrami–Kolmogorov) equation is exponential equation inserted power-law behavior on the parameter, and is widely utilized to describe the relaxation process, the nucleation process, the deformation of materials and so on. Theoretically the power exponent is occasionally associated with the geometrical factor of the nucleus, which gives the integral power exponent. However, non-integral power exponents occasionally appear and they are sometimes considered as phenomenological in the experiment. On the other hand, the power exponent decides the distribution of step time when the equation is considered as the superposition of the step function. This work intends to extend the interpretation of the power exponent by the new method associating Shannon entropy of distribution of step time with the method of Lagrange multiplier in which cumulants or moments obtained from the distribution function are preserved. This method intends to decide the distribution of step time through the power exponent, in which certain statistical values are fixed. The Shannon entropy to which the second cumulant is introduced gives fractional power exponents that reveal the symmetrical distribution function that can be compared with the experimental results. Various power exponents in which another statistical value is fixed are discussed with physical interpretation. This work gives new insight into the JMAK function and the method of Shannon entropy in general.

1. Introduction

The stretched exponential function is described as follows,

$$f\left(t,K,\beta \right)=exp\left[-{\left(\frac{t}{K}\right)}^{\beta }\right].$$

(1)

It is widely applied to describe relaxation processes [1,2,3,4,5], kinetics of crystallization [6,7,8,9], deformations of materials [10,11] and so on. The name “stretched exponentials” corresponds to the case for $\beta <1$, while the opposite case of $\beta >1$ is called the “compressed exponential function”. The latter case corresponds to the JMAK (Johnson–Mehl–Avrami–Kolmogorov) equation [6,7,8,9], and $\beta$ is sometimes called the Avrami constant. In the context of the JMAK equation, theoretically it is occasionally associated with the geometrical factor of the nucleus. The Avrami constant $\beta$ originates from the dimensionality in which nucleation occurs D, which has the following relation, $\beta =D+1$. The surface nucleation involving effectively two dimensions gives $\beta =3$; the homogeneous nucleation with three dimensions gives $\beta =4$; they should be integral constant [12]. However, occasionally non-integer, anomalous Avrami constants are found [13,14,15]. This anomalousness is explained thorough the heterogeneity of dimensionality of nucleation, and the distribution of pre-existing nuclei, and the nucleation rate [16,17,18,19]. The limitation to associating the JMAK model with the dimensionality of the nucleus is designated [20]. These works suggest that JMAK equations still demand interpretations.

On the other hand, Equation (1) mathematically corresponds to the Weibull distribution in extreme value theory [21,22,23]. It is the probability distribution function of which the rate of occurrence of events varies with time, applied to the particle distribution and the failure analysis for engineering. In this context, the power exponent $\beta$ controls the shape of the distribution of the event; it is sometimes called the shape parameter [24]. The time-compressed equation corresponds to Weibull distribution, of which the rate of occurrence of the event increases with time. Hence, the power exponents decide the distribution of occurrence.

It is suggested that theoretical models for Equation (1) involve the spatial-temporal heterogeneity. The hierarchical constrained model involves the constraints among Ising spins [25]; the trap model involves the traps in the space in which Brownian motion occurs [26]. Evesque demonstrated that the reaction of two molecules in fractal geometry gives the fractional power exponent for Equation (1) [27].

Based on these reports and the fact that $\beta$ decides the distribution, a new method of estimating the distribution is proposed, using Shannon entropy [28]. Shannon entropy [29] is utilized for the probability density function to estimate the average amount of information content of the distribution, which reflects the statistical homogeneity. Introducing Shannon entropy into the distribution function obtained from Equation (1), it was found that the Shannon entropy to which the first moment is introduced has a supremum at $\beta =1$; it corresponds to single exponentials [28]. This result includes the insight on the relation between stretched exponentials and single exponentials.

This method is suggestive of the application of Shannon entropy into the kinetic equations. Analyzing the method carefully, it consists of the maximum entropy estimation and Lagrange multiplier with $\beta$ as a parameter. The maximum entropy method is applied to estimate the optimal distribution [30,31,32]. However, this method is different from general maximum entropy estimation [32] on the point that the fundamental distribution function is already fixed as Equation (1). The optimal shape of distribution is estimated via $\beta$ while the constraint condition is introduced. This method decides the $\beta$ that gives optimal distribution of step times, which depends on the given boundary condition.

Herein, this work intends to extend the previous method and to attempt to explore the distributions of Equation (1) in which certain statistical quantities are fixed. Then we attempt to discuss the physical interpretation for obtained distributions.

2. Method: Maximum Entropy Estimation Method Based on the JMAK Equation

The point that it is different from general maximum entropy estimation [32] is that the form of the equation is already fixed in Equation (1), the JMAK equation. Thus, here we call this method the maximum entropy estimation method based on the JMAK equation. The method consists of two procedures. First is the introduction of Shannon entropy into the compressed exponential equation, Equation (12). Second is the introduction to the statistical quantity which corresponds to the restricted condition.

At first, the integral equation is assumed as,

$$exp\left[-{\left(\frac{t}{K}\right)}^{\beta }\right]={\int }_0^{\infty }D\left(\tau \right)F\left(t-\tau \right)d\tau$$

(2)

where $F\left(t-\tau \right)$ is the step function. Then the distribution function $D\left(\tau \right)$ is obtained as follows,

$$D\left(\tau ,K,\beta \right)=\frac{\beta }{K}{\left(\frac{\tau }{K}\right)}^{\beta -1}exp\left[-{\left(\frac{\tau }{K}\right)}^{\beta }\right].$$

(3)

Shannon entropy is defined as,

$$H\left(K,\beta \right)={\int }_0^{\infty }D\left(\tau ,K,\beta \right)ln\frac{D\left(\tau ,K,\beta \right)}{C}d\tau$$

(4)

where C is the constant for nondimensionalization. Then the Shannon entropy of Equation (3) is given as follows,

$$H\left(K,\beta \right)=\gamma \left(1-\frac{1}{\beta }\right)+ln\frac{CK}{\beta }+1$$

(5)

where $\gamma$ is Euler constant. Now $H\left(K,\beta \right)$ is a function with two parameters K and $\beta$. To introduce the constraint condition, K is now related with parameter $\beta$. A certain statistical quantity $〈\xi 〉$, which is obtained using Equation (3), is given as

$$〈\xi 〉=\Phi \left(K,\beta \right).$$

(6)

For example, $〈\xi 〉$ is the first moment when $\Phi \left(K,\beta \right)={\int }_0^{\infty }\tau D\left(\tau ,K,\beta \right)d\tau$. As $〈\xi 〉$ is constant, Equation (6) can be reformalized as

$$K=K\left(〈\xi 〉,\beta \right).$$

(7)

Now $K=K\left(〈\xi 〉,\beta \right)$ is a function with one parameter $\beta$. Following the Lagrange multiplier method, then we have

$$H\left(K,\beta \right)=H\left[K\left(〈\xi 〉,\beta \right),\beta \right]=H\left(\beta ,〈\xi 〉\right).$$

(8)

Equation (8) is the Shannon entropy of which the statistical quantity $〈\xi 〉$ is fixed. In order to get optimal distribution, the supremun of Equation (8) is identified as follows,

$$H\left({\beta }^{*},〈\xi 〉\right)=\underset{\beta }{sup}H\left(\beta ,〈\xi 〉\right).$$

(9)

${\beta }^{*}$ gives the optimal distribution in which $〈\xi 〉$ is fixed.

3. Result and Discussion

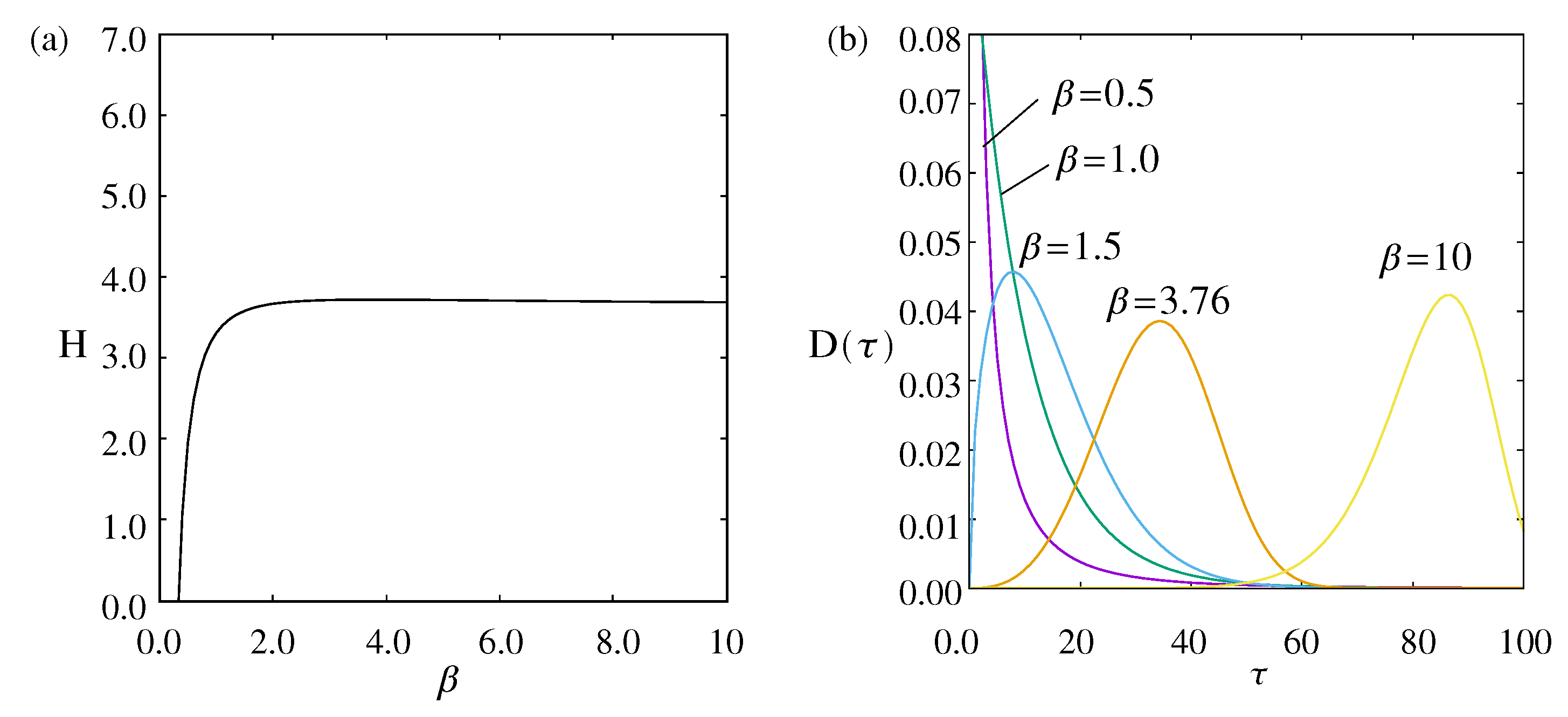
3.1. Constraint Condition of n-th Moment

In the previous work, the first moment was introduced to Shannon entropy Equation (5) to find ${\beta }^{*}=1$ [28]. Here we discuss the case in which other moments (e.g., third moment, n-th moment) are fixed. The moment gives the information of the shape of the function. The first moment is the mean value, the second moment is related with the variance and so on.

The n-th moment of Equation (3) is given as

$$〈K^n〉={\int }_0^{\infty }{\tau }^{n}D\left(\tau ,K,\beta \right)d\tau =\frac{K^n}{\beta }\Gamma \left(\frac{n}{\beta }\right)$$

(10)

where $\Gamma \left(x\right)$ is Gamma function.

By introducing the n-th moment of Equation (3) into Equation (5), we have

$$H\left(\beta ,〈K^n〉\right)=\gamma \left(1-\frac{1}{\beta }\right)-\frac{1}{n}ln\Gamma \left(\frac{n}{\beta }\right)+\left(\frac{1}{n}-1\right)ln\beta +lnC{\langle K^n\rangle }^{1/n}+1$$

(11)

We can easily estimates ${\beta }^{*}$ by differentiating above Equation (12) as follows,

$$\frac{dH\left(\beta ,〈K^n〉\right)}{d\beta }=\frac{1}{{\beta }^2}\left[\gamma +\psi \left(\frac{n}{\beta }\right)+\beta \left(\frac{1}{n}-1\right)\right]$$

(12)

where $\psi \left(x\right)$ is the Digamma function. ${\beta }^{*}$ of each n-th moment are listed in

Table 1. Table of each ${\beta }^{*}$ in which the entropy is maximized in each n-th moment.

n	${\mathit{\beta }}^{*}$
1	1
2	1.2994
3	1.5
4	1.6533
5	1.7784
10	2.1981
100	3.8527
1000	5.7403

. ${\beta }^{*}$ increases with n and they are fractional numbers except for $n=1$ and 3. These results seem trivial but the third moment can be related to volume in the case that t has space dimension. Rosin–Rammler distribution [33], which corresponds to Equation (1), is applied for particle distributions. Rosin–Rammler distribution has $\beta >1$. These moments can be related to physical quantity through the distribution function.

3.2. Constraint Condition of Second Cumulant: Variance

Now let us see the Shannon entropy to which the variance of Equation (1) is introduced. The variance of Equation (1) is

$${\sigma }^2=K^2\left[\Gamma \left(1+\frac{2}{\beta }\right)-\Gamma {\left(1+\frac{1}{\beta }\right)}^2\right].$$

(13)

Introducing Equation (13) into Equation (5), we have Shannon entropy of which the variance is fixed,

$$H\left(\beta ,{\sigma }^2\right)=\gamma \left(1-\frac{1}{\beta }\right)-ln\beta -\frac{1}{2}ln\left[\Gamma \left(1+\frac{2}{\beta }\right)-\Gamma {\left(1+\frac{1}{\beta }\right)}^2\right]+lnC\sqrt{{\sigma }^2}+1.$$

(14)

The relation of H and $\beta$ is described in Figure 1a. The absolute value of H is relative depending on C. Continuous Shannon entropy is relative to the coordinate system. Here we are interested in the relative value of entropy, particularly the supremum value. $\beta$ that give a supremum of H is $3.7673\cdots$ though H show a plateau over $\beta \simeq 3$. Interestingly, $\beta$ that have large values of entropy seems to be related with symmetry of distribution as Figure 1b shows. The $\beta$ with lower entropy (e.g., $\beta =0.5\sim 1.5$) give asymmetric distribution of $\tau$ while $\beta$ with larger values ($\beta =3.76\sim 10$) give symmetric distribution.

The relation between distribution and variance was suggested in the relaxation of the shrink of PNIPA gels [34]. The relaxation process of PNIPA gels involves two-step shrinking. The first shrink undergoes a diffusion process that was described with a single exponential while the second shrink can be described as a compressed exponential having $\beta =2\sim 4.5$. These reported $\beta$ have the largest Shannon entropy, which suggests a correspondence. In the shrinkage of PNIPA gels, each part of the gels undergoes the step-like shrinkage, which corresponds to a step-function. However, it is expected that the timing of shrinkage has variations, which results in symmetric distribution. This interpretation reinforces that the JMAK relaxation of PNIPA gels involves the process in which the variance is fixed.

3.3. Constraint Condition of Third Cumulant: Skewness

The third cumulant, skewness, reflects the asymmetry of distribution. The third cumulant is obtained as follows,

$$c^3=K^3\left[\frac{1}{\beta }\Gamma \left(\frac{3}{\beta }\right)-\frac{3}{{\beta }^3}\Gamma \left(\frac{2}{\beta }\right)\Gamma \left(\frac{1}{\beta }\right)+\frac{2}{{\beta }^3}\Gamma {\left(\frac{1}{\beta }\right)}^3\right].$$

(15)

By introducing Equation (15) into the Shannon entropy equation, Equation (5), in the same way, we can estimate the Shannon entropy of which skewness is fixed as

$$H\left(\beta ,c^3\right)=\gamma \left(1-\frac{1}{\beta }\right)-\frac{1}{3}ln{\beta }^3\left[\frac{1}{\beta }\Gamma \left(\frac{3}{\beta }\right)-\frac{3}{{\beta }^3}\Gamma \left(\frac{2}{\beta }\right)\Gamma \left(\frac{1}{\beta }\right)+\frac{2}{{\beta }^3}\Gamma {\left(\frac{1}{\beta }\right)}^3\right]+lnC\sqrt[3]{c^3}+1.$$

(16)

Figure 2a is the dependence of Shannon-entropy introduced skewness with $\beta$. ${\beta }^{*}$ has a value around $1.20$ and decreases monotonically. The distributions of $\tau$ having $\beta =0.5,1.2,3.76$ are compared in Figure 2b.

${\beta }^{*}$ seemingly gives positive skewed distribution. Negative skew distribution has to be asymmetric for the left side, but this is not possible for Equation (3).

4. Conclusions

In this work, the new method to obtain the distribution is attempted using Shannon entropy. The point that it is different from general maximum entropy estimation [32] is that the form of the equation is already fixed in Equation (1), the JMAK equation. The Shannon entropy of the JMAK equation was firstly estimated using distribution function $D\left(\tau \right)$, which is obtained by an integral equation of which Kernel $F(t-\tau )$ is a step function. Introducing the certain statistical quantity, the Shannon entropy of which the quantity is fixed was estimated. The optimal distributions are obtained by identifying ${\beta }^{*}$, which is a $\beta$ that gives a supremum of H.

The Shannon entropies that are introduced n-th moments give fractional power exponents except for the first and third moments. The Shannon entropy to which variance is introduced shows a plateau over $\beta =3$. The value of the entropy seems to reflect the symmetry of the distribution of step times. The power exponents observed in the shrinking of PNIPA gels have a value around $2\sim 4.5$, which corresponds to the distribution of the largest entropies. The Shannon entropy with the third cumulant where skewness is introduced has a supremum at ${\beta }^{*}=1.20$, which gives positive-skewed distribution.

The Shannon entropies whose variance or skewness is introduced are quite interesting as their ${\beta }^{*}$ seems to give a distribution in which the constraint condition, variance and skewness is typically fixed. There is an interpretation of maximum entropy. The Kolmogorov–Sinai theorem [35] says that the partition obtained by maximum entropy gives the smallest subsets of the generator. The distribution of $\tau$ corresponds to the partition of step times. If we follow the theorem, these distributions give the generator in which constraint conditions, variance or skewness are fixed. The relation and interpretation based on the Kolmogorov–Sinai theorem should be pursued for further development.

The method to decide $\beta$ using Shannon entropy with Lagrange multipliers gives the optimal distribution, the physical quantity of which is fixed. The phenomena described by JMAK type equations may involve these constraint conditions.