Stochastic Mechanical Characterization of Polysilicon MEMS: A Deep Learning Approach ^†

Abstract

Deep Learning strategies recently emerged as powerful tools for the characterization of heterogeneous materials. In this work, we discuss an approach for the characterization of the mechanical response of polysilicon films that typically constitute the movable structures of micro-electro-mechanical systems (MEMS). A dataset of microstructures is digitally generated and a neural network is trained to provide the appropriate scattering in the values of the overall stiffness (in terms of the Young’s modulus) of the grain aggregate. Since results are framed within a stochastic procedure, the aim of the learning strategy is not to accurately reproduce the microstructure-informed response of the polysilicon film, but instead to provide a fast tool to be used at the device level for Monte Carlo analysis of the relevant performance indices. Accuracy of the proposed approach is assessed for very small samples of the polycrystalline aggregate to check if size effects are correctly captured.

1. Introduction

Paths toward further miniaturization for semiconductor technologies may pose issues in the prediction of the relevant performances of micro-devices like micro-electro-mechanical systems MEMS [1,2,3]. Usually, the geometrical and physical properties of the devices are assumed to be known in a deterministic sense; in reality, uncertainties are unavoidable and may become dominant as a result of the micro-fabrication process [4,5,6,7].

For polysilicon MEMS, the effects of the crystalline morphology on the reliability of inertial devices subjected to impacts and also under operational conditions were studied by the authors in [8,9,10,11,12,13,14,15,16] to possibly drive their optimization. To characterize the micro-devices on the basis of real experimental data, an on-chip test procedure was also proposed and analyzed in [17,18,19,20]. By varying the length of the tested film samples and the experimental setup, the effects of the polycrystalline morphology and of the overetch depth on the device response to actuation were assessed.

The aforementioned approach allowed the building of a complex and effective methodology to characterize both the device and the polysilicon film constituting its movable structure. Due to the interplay between film morphology and the outcome of the etching stage of micro-fabrication, if the stiffness of the film itself is the goal of the investigation, statistical Monte Carlo analyses are required every time the geometrical features of the device are varied. This results in a time-consuming procedure, and strategies to avoid it are therefore to be envisioned. A possible approach could be to adopt interpolating functions among the available data—for instance, via polynomial chaos expansion (PCE)-based procedures; see, e.g., [21]. A novel approach, accounting for the recent development and burst in applications of artificial intelligence tools, can instead be based on neural networks (NNs) and machine/deep learning [22,23,24].

As for the adoption of deep learning for data assimilation and, specifically, for assessing the effective properties of micro-structured materials, interesting results were recently discussed in [25,26]. Here, we propose a different approach in two distinctive directions: The NN is not trained to perfectly reproduce the results in terms of overall elastic properties of the film for any stochastic representation of it—termed the statistical volume element (SVE)—but instead to catch the statistical distributions of the mentioned properties; the NN is trained with a procedure similar to those adopted for image recognition, hence by handling a pool of pictures of the morphology of the film only. Results are compared to those attained with a standard, semi-analytical homogenization procedure to bound the effective film elasticity in order to start assessing the accuracy and the efficiency of the proposed approach.

2. Effective Properties of Polysilicon Films: Homogenization Approach

The effective elastic properties of a polysilicon film are accounted for here through the value of the Young’s modulus $E$ of the grain aggregate. Since the effects of the film morphology have to be evaluated, we adopt a semi-analytical strategy to obtain estimations of the microstructure-informed probability distribution of $E$ by bilaterally bounding it for film samples featuring a finite size. To assess the morphology-induced scattering, a Monte-Carlo-driven homogenization procedure is proposed. This approach somehow merges the features of purely analytical and numerical ones, as discussed in previous works [13,14], so that finite element solutions are not required to infer the aforementioned statistics of $E$.

We specifically account for the columnar structure of the epitaxially grown polycrystalline film with a texture aligned with the out-of-plane direction, as seen in Figure 1. As the scattering of $E$ around the mean value turns out to be size dependent—namely, a function of the ratio between the in-plane size $h$ of the polysilicon aggregate and the characteristic size $s_g$ of the grains—the asymptotic approach discussed in [14] is not further investigated here. Bounds are based on the Voigt and Reuss assumptions, which assume that for each SVE, either the strain or the stress state is uniform throughout the polycrystalline sample. Moving from the Hill–Mandel condition, under the Voigt assumption of a uniform strain field, the effective stiffness matrix is bounded by:

$$\mathit{C}=\frac{1}{\mathsf{\Omega }}{\int }_{\mathsf{\Omega }}{\mathit{t}}_{\xi }^{\mathrm{T}}{\mathit{c}}_l{\mathit{t}}_{\xi }^{}\mathrm{d}\mathsf{\Omega }={\sum }_{i=1}^N\frac{{\mathsf{\Omega }}_i}{\mathsf{\Omega }}{\mathit{t}}_{i,\xi }^{\mathrm{T}}{\mathit{c}}_l{\mathit{t}}_{i,\xi },$$

(1)

while under the Reuss assumption of a uniform stress field, the effective compliance matrix is bounded by:

$${\mathit{C}}^{-1}=\frac{1}{\mathsf{\Omega }}{\int }_{\mathsf{\Omega }}{\mathit{t}}_{\sigma }^{\mathrm{T}}{\mathit{c}}_l^{-1}{\mathit{t}}_{\sigma }\mathrm{d}\mathsf{\Omega }={\sum }_{i=1}^N\frac{{\mathsf{\Omega }}_i}{\mathsf{\Omega }}{\mathit{t}}_{i,\sigma }^{\mathrm{T}}{\mathit{c}}_l^{-1}{\mathit{t}}_{i,\sigma }.$$

(2)

In these equations: $\mathsf{\Omega }$ is the volume of the entire SVE; ${\mathsf{\Omega }}_i$ is the volume of the $i$-th grain, with $i=1,\dots ,N$ and $N$ being the number of grains gathered by the SVE; ${\mathit{c}}_l$ is the in-plane single-crystalline silicon stiffness matrix in a local reference frame aligned with the axes of elastic symmetry; ${\mathit{t}}_{i,\sigma }$ and ${\mathit{t}}_{i,\xi }$ are the orthogonal transformation matrices relevant to the $i$-th grain, which respectively allow the transformation of the stress and strain vectors from the global reference frame to the one aligned with the axes of elastic symmetry. As the grain lattice orientation is a piecewise constant field within the SVE, the integrals in Equations (1) and (2) can be re-written as shown in terms of a sum of contributions from the $N$ grains in the sample.

As the length-scale separation principle adopted to define the properties of a representative volume element of polycrystalline materials is supposed not to hold true in our analysis due to the small $h/s_g$ ratio, SVE geometries are adopted to feed a Monte Carlo procedure. Within it, stochastic effects on the SVE geometry are provided in terms of: Topology of the network of grain boundaries and lattice orientation of each grain. Each SVE is generated using a regularized Voronoi tessellation; see [8].

3. Effective Properties of Polysilicon Films: Neural Network Approach

An NN works through non-linear combinations of adaptive basis functions [22]. During a training phase, within which data are fed to the NN, such basis functions are tuned by means of parameters called weights. By exploiting a convolutional NN, which performs convolutional and pooling operations, we can recognize statistical patterns in images representing the morphology of the polysilicon film, and also find a correlation between it and its effective elastic properties.

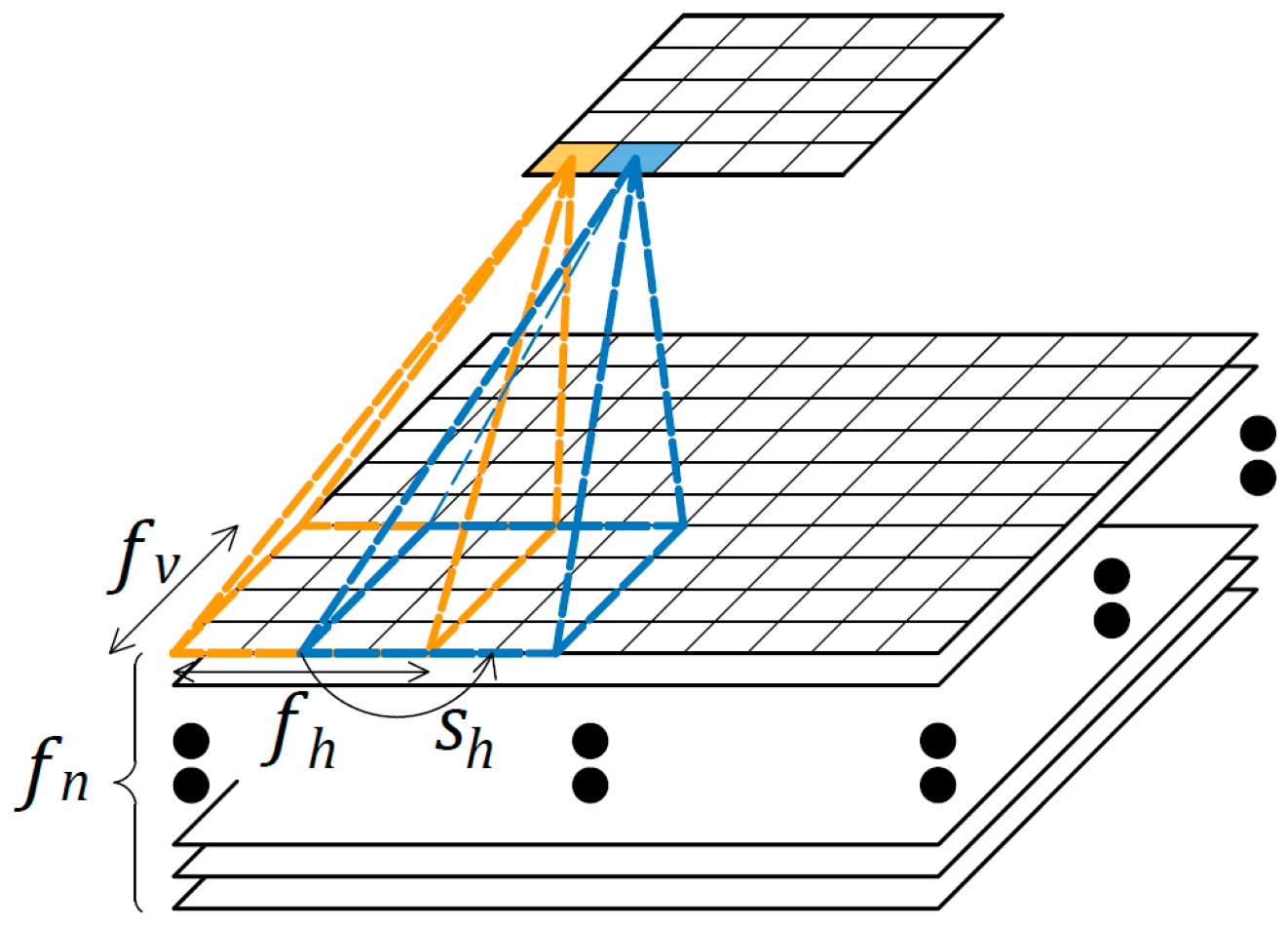
A deep NN architecture is characterized by several layers, each one performing a data transformation. A special transformation is performed by the convolutional layers, whose weights, called filters, are connected to a small (bi-dimensional) receptive field of the incoming inputs. The height $f_v$ and width $f_h$ of the filters are used to set the dimensions of the receptive fields in the two in-plane directions. The outputs of a convolutional layer are called feature maps; within a feature map, all of the neurons share the same filter. A schematic representation of the receptive field of a convolutional layer is depicted in Figure 2. To reduce the dimension of the output and, therefore, render the NN more computationally efficient, one may apply a stride, which is like setting a distance between two consecutive receptive fields; two different strides, $s_v$ and $s_h$, may be adopted in the two in-plane directions. Accordingly, in each single convolutional layer, the input and output are linked through:

$$z_{i,l,k}^{conv}=b_k+{\sum }_{u=0}^{f_h-1}{\sum }_{v=0}^{f_v-1}{\sum }_{k=0}^{f_n-1}{x}_{\iota ,\lambda ,\kappa }{w}_{u,v,k,\kappa }\mathrm{with}\{\begin{array}{c}\iota =i{s}_h+u\\ \lambda =l{s}_v+v\end{array},$$

(3)

where: $z_{i,l,k}^{conv}$ is the output of the convolutional layer located in the $i$-th row and $l$-th column of the $k$-th feature map; $b_k$ is the bias of the $k$-th feature map; $x_{\iota ,\lambda ,\kappa }$ is the input located in the $\iota$-th row and $\lambda$-th column of the $\kappa$-th feature map of the input layer; $w_{u,v,k,\kappa }$ is the $\left(u,v\right)$-th connection weight of the $k$-th filter applied to the $\left(\iota ,\lambda \right)$-th input of the $\kappa$-th feature map of the input layer.

The other important building block of the employed NN architecture is the pooling layer. Like in a convolutional layer, here, each neuron is connected to a small receptive field; it is therefore necessary to define the receptive field dimensions, $f_v$ and $f_h$, and the strides, $s_v$ and $s_h$. At variance with a convolutional layer, a pooling neuron has no weights; often, it works on every input channel independently: It is then used to reduce the dimensionality of the inputs, to limit the computational burden, and to avoid overfitting. Two pooling mechanisms are used in practice: Max pooling and average pooling. In the former case, only the greatest entry of each receptive field is passed to the next layer, as follows:

$$z_{i,l,k}^{pool}=\max \left\{x_{\iota ,\lambda ,k}\right\}\mathrm{with}\{\begin{array}{c}\iota =i{s}_h+u\mathrm{for}u=0,\dots ,\left(f_h-1\right)\\ \lambda =l{s}_v+v\mathrm{for}v=0,\dots ,\left(f_v-1\right)\end{array},$$

(4)

where: $z_{i,l,k}^{pool}$ is the output of the max pooling layer located in the $i$-th row and $l$-th column of the $k$-th transformed feature map; $x_{\iota ,\lambda ,\kappa }$ is the input located in the $\iota$-th row and $\lambda$-th column of the $k$-th input feature map. The input and the transformed feature map have been labelled in the same way to stress the one-to-one correspondence resulting from the pooling operation. In the latter case, the pooling layer works in the same way but, instead of selecting the greatest entry in the receptive field, it computes the corresponding average value.

Very deep NN architectures may lead to the so-called degradation problem; a deep NN may result in less accuracy than a shallow one, since not all of the NNs are equally easy to handle due to the intrinsic difficulties related to huge stacks of nonlinear layers. For this reason, a deep residual learning framework was recently proposed: By denoting with $x$ the input of the stacked layers and with $H\left(x\right)$ the underlying function to be approximated, shortcut connections lead to approximately $F\left(x\right)≔H\left(x\right)-x$. Additional details of the whole NN architecture and of the learning strategy will be reported elsewhere.

In concrete terms, during training, the convolutional layers correlate the information present in the images, consisting of the geometry of grain boundaries and a color code to denote the lattice orientation of each grain, with the effective Young’s modulus E. This task proves demanding for the NN architecture, given that an extremely local information like a grain boundary must be translated into a global characterization of the image, and it can be tackled through convolutional layers. Indeed, once the filter of a feature map has learned how to detect a grain boundary with a specific orientation in an SVE, this filter can detect boundaries with the same orientation in every region of the other SVE images.

4. Results

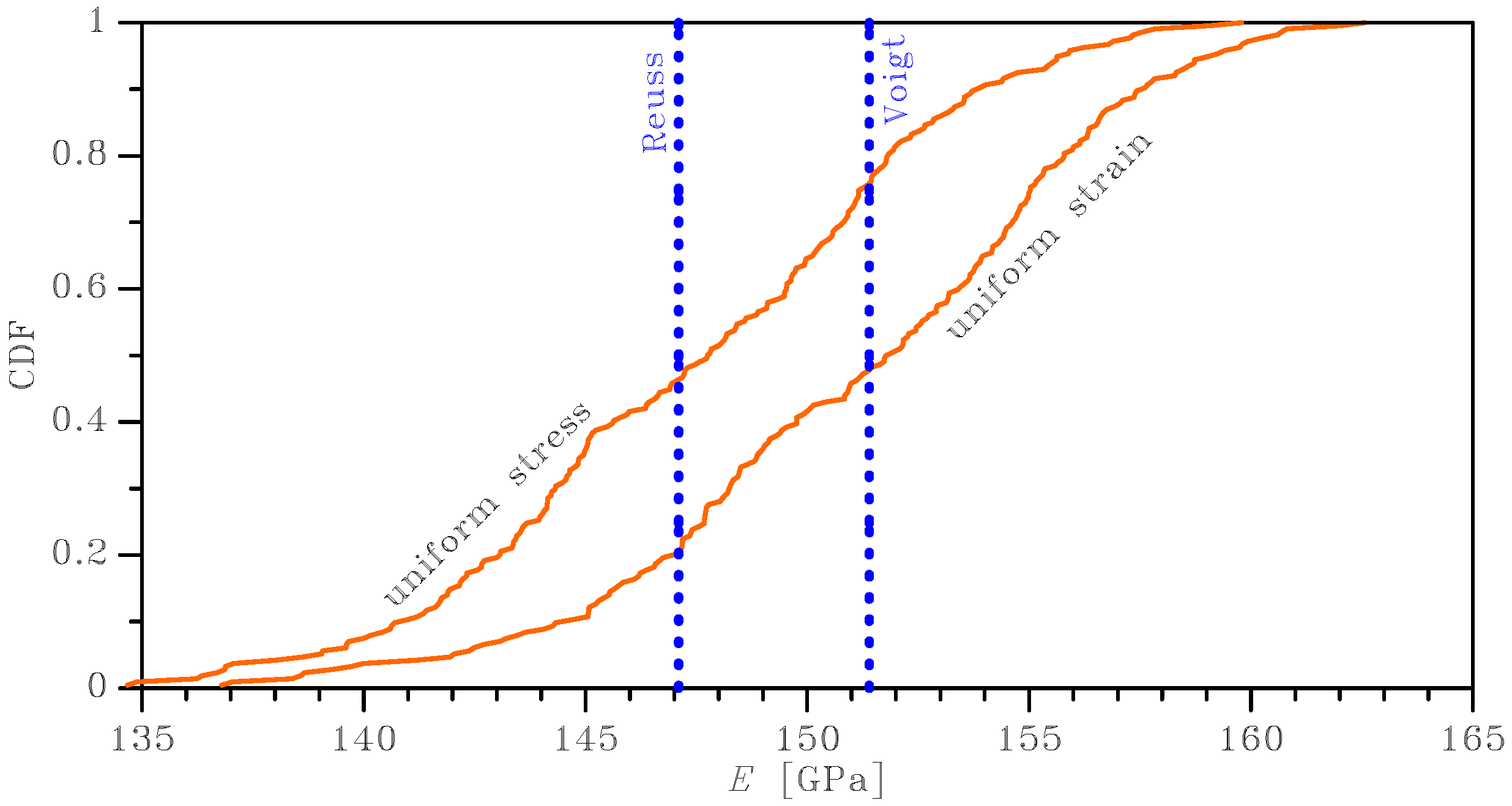
Representative results in terms of the cumulative distribution functions bounding $E$, relevant to the two assumptions concerning the uniformity of the solution within the SVE, are shown in Figure 3 for $h=2$ μm and $s_g=0.5$ μm. In this graph, the blue vertical lines represent the two asymptotic bounds obtained by assuming that the ratio $h/s_g$ grows to infinity, hence with a perfectly uniform distribution of the lattice orientation of the grains in the SVE. The mean value $E_m$ and standard deviation $E_s$ for the obtained effective Young’s modulus are: Under the Voigt assumption, $E_m=150.0$ GPa, $E_s=5.5$ GPa; under the Reuss assumption, $E_m=148.1$ GPa, $E_s=5.4$ GPa. An interesting feature of these results is that the mean values are very close to the average between the asymptotic Reuss and Voigt bounds; in [27], it was shown that the scattering in the solution around the mean is instead greatly affected by $h/s_g$. Similar results can also be attained for the other elastic moduli of the film, assumed to be in-plane isotropic (namely, transversely isotropic with the mentioned texture aligned with the out-of-plane direction) at varying $h/s_g$ ratios.

Since the discussed homogenization procedure has to be repeated every time the $h/s_g$ ratio is varied, accounting for the morphological film effects can result in a time-consuming procedure. The described novel approach based on NNs, devised in order to learn the stochastic effects on the basis of some representative SVE geometries, thought of as an optimal and minimal pool of datasets, is therefore going to provide information on the statistical distributions of the effective properties for any size of the polycrystal.

The convolutional NN adopted in the current work is based in the ResNet-18 architecture; additionally, a 50% dropout layer was added after the flattened layer as a method of regularization to improve the generalization capability of the NN and also to reduce overfitting of the training data. A linear activation function is assigned to the output layer in order to allow the intended regression task: The prediction of the effective Young’s modulus for each SVE is obtained by feeding 256 × 256 pixel images representing the polysilicon microstructures. The NN is used to extract the relevant features intrinsically encoded in the images—which are the areas and shapes of the grains, the relative locations of neighboring grains, and the lattice orientations—to finally build a regression model exploiting the previously labeled or ground-truth data.

Overall, $n=192$ SVEs are considered in the analysis. The images are split into two subsets, 75% for training and 25% for validation. Similarity transformations (rotations and flips, maintaining the consistency with the ground-truth data) are also adopted as data augmentation regularization. In the implementation, batches of 32 images are used to reduce the computational cost during training, considering also that the stochastic gradient descent method operates in a small-batch regime wherein a fraction of the training data is sampled to approximate the gradient [28].

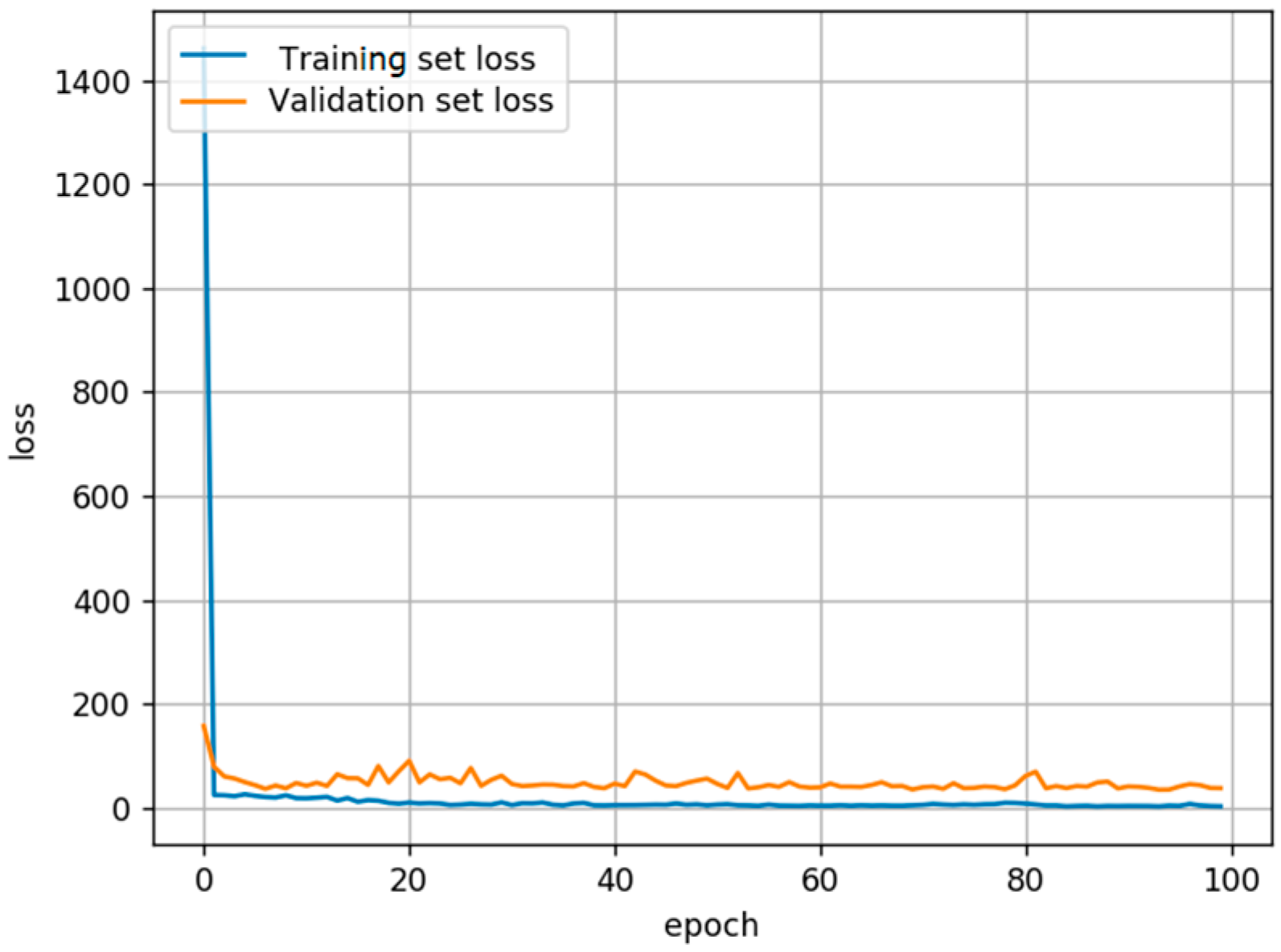
The training of the NN aims at the minimization of a loss function that quantifies the prediction error via the adaptive moment estimation (Adam) optimization algorithm. The Mean Squared Error (MSE) function is selected for this matter; it is given as the average of the squared differences between the labels $y_i$ and the predicted values ${\widehat{y}}_i$, according to:

$$\mathrm{MSE}=\frac{1}{n}{\sum }_{i=1}^n{\left(y_i-{\widehat{y}}_i\right)}^2.$$

(5)

Due to the quadratic dependency in Equation (5), the penalization is larger for the predicted values laying far from the corresponding ground-truth data. The evolution of the training process in terms of variations of the loss function values for the training and validation datasets is shown in Figure 4.

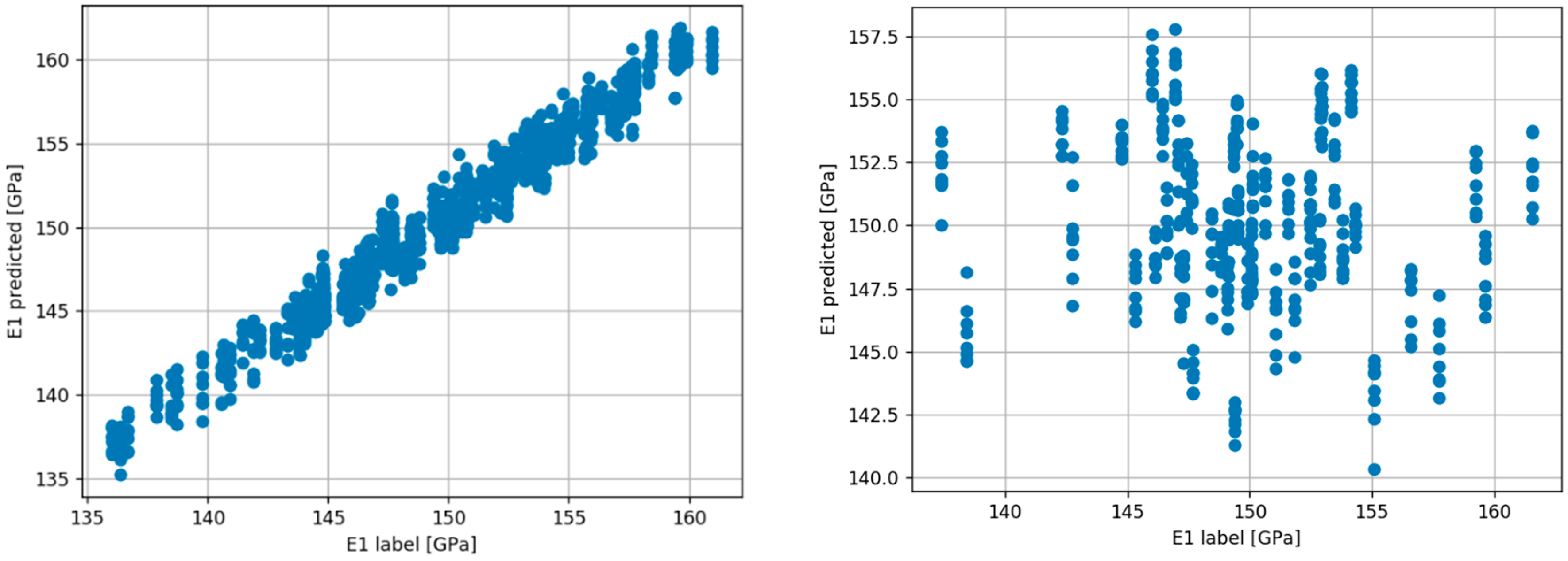
An assessment of the results is provided in Figure 5, in terms of the predicted values of the effective Young’s modulus and the ground-truth data, both for training and validation. In these graphs, the ideal outcome would be represented by a 45 degree line corresponding to a perfect match between predicted and ground-data values. As typically occurs, the results obtained over the training set outperform those obtained over the validation set. The statistical indicators of the ground-truth data, regarded as the direct target of the regression task, are $E_m=149.7$ GPa and $E_s=5.5$ GPa for the training set, and $E_m=149.9$ GPa and $E_s=4.8$ GPa for the validation set. The ones obtained with the NN turn out to be $E_m=150.5$ GPa and $E_s=5.5$ GPa for the training set, and $E_m=150.0$ GPa and $E_s=3.4$ GPa for the validation set; hence, further work is needed in order to improve the generalization accuracy of the NN.

5. Conclusions

In this paper, we have proposed an approach based on neural networks and deep learning for the assimilation of data from a set of two-dimensional digital representations of polycrystalline geometries, in order to infer the statistics of the effective elastic moduli of the grain aggregate with a minimal computational effort. A strength of the procedure, though not assessed here explicitly, is that size effects can be automatically set in if the neural network is trained with polycrystalline geometries featuring varying dimensions relative to the characteristic grain size.

In future works, results relevant to all of the elastic properties will be reported. Furthermore, the neural network architecture will be optimized in order to attain a higher accuracy, still with a minimal computational cost.