Acoustic Location of Bragg Peak for Hadrontherapy Monitoring †
Abstract
1. Introduction
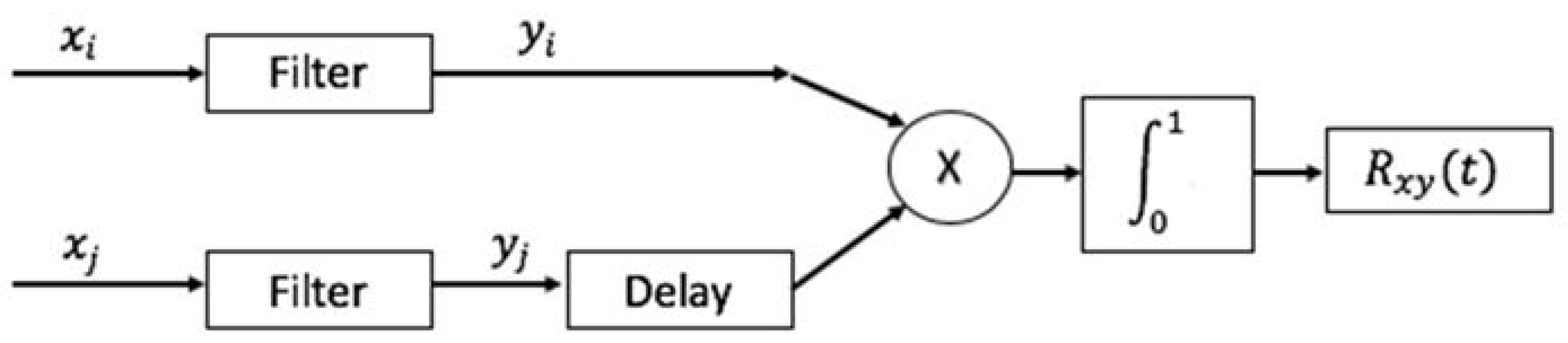
2. Overview of Approach
3. Studies and Results
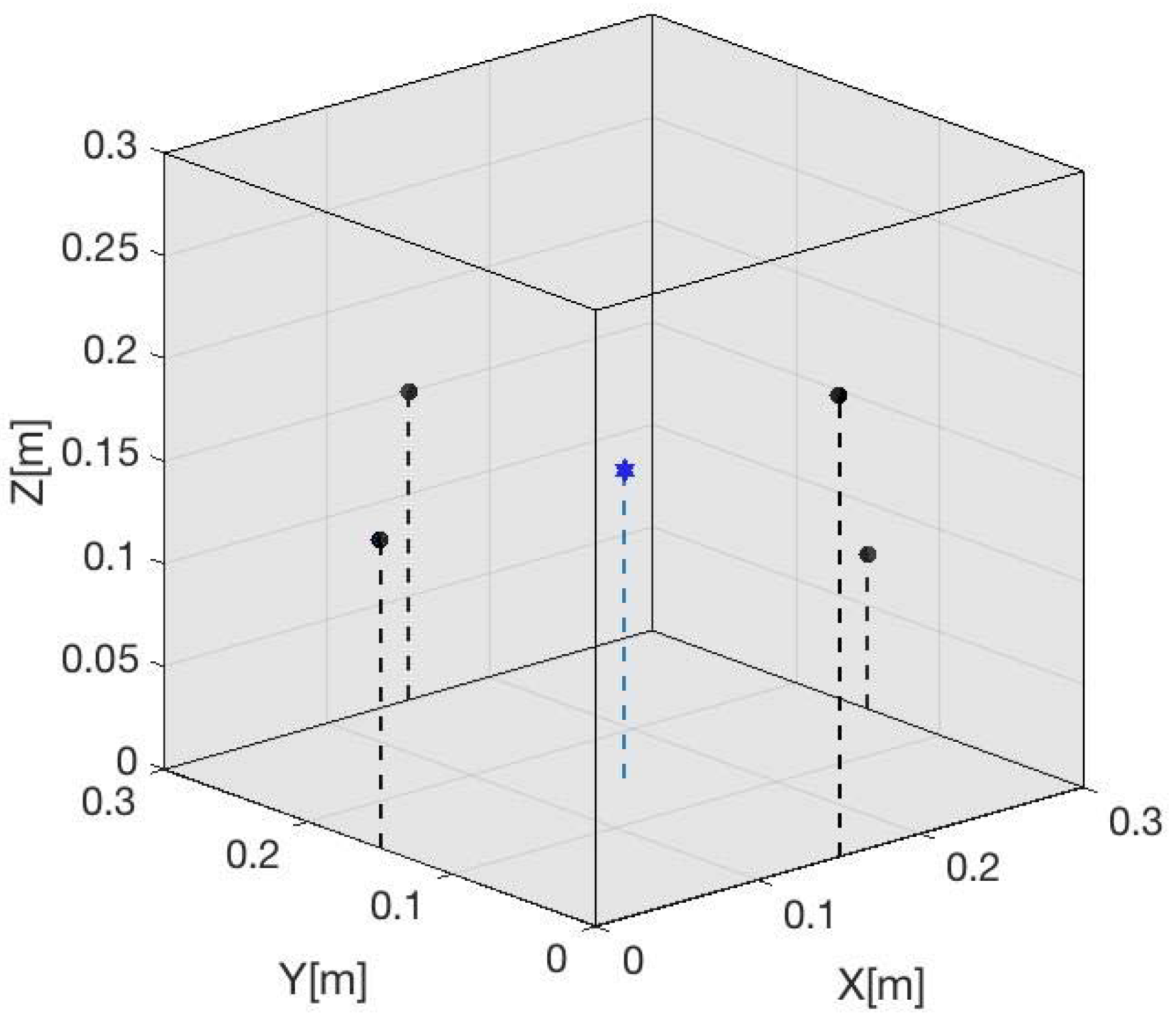
3.1. Numerical Simulation
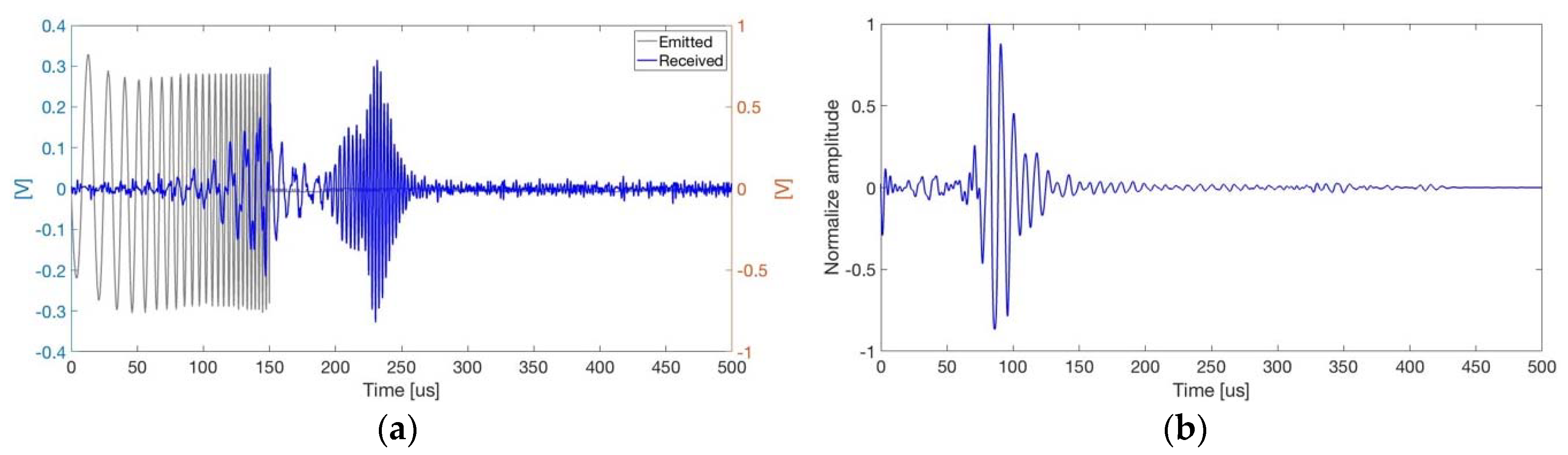
3.2. Experimental Localization with Armonic Signals
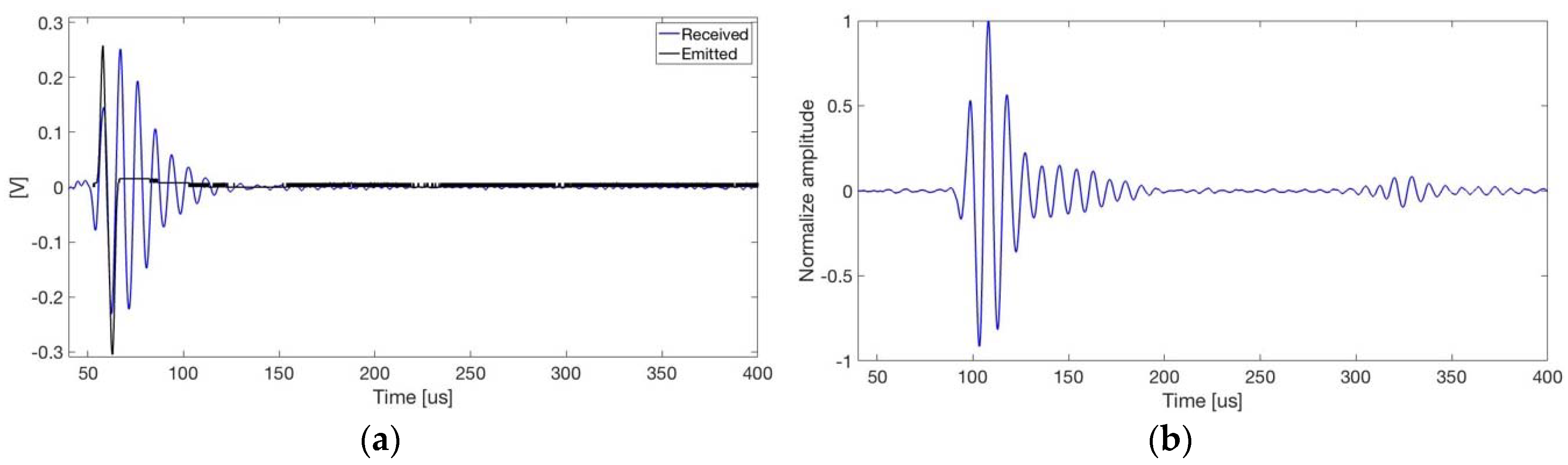
3.3. Experimental Localization with Thermoacoustic Signals
4. Conclusions
Conflicts of Interest
References
- Kundu, T. Acoustic source localization. Ultrasonics 2014, 54, 25–38. [Google Scholar] [CrossRef] [PubMed]
- Moore, D.; Leonard, J.; Rus, D.; Teller, S. Robust distributed network localization with noisy range measurements. In Proceedings of the 2nd international conference on Enbedded networked sensor systems, Baltimore, MD, USA, 3–5 November 2004. [Google Scholar]
- Niculescu, D.S. Ad Hoc Positioning System (APS). In Proceedings of the Global Telecommunications Conference, San Antonio, TX, USA, 25–29 November 2001. [Google Scholar]
- Bortfeld, T. An analytical approximation of the Bragg curve for therapeutic proton beams. Med. Phys. 1998, 24, 2024–2033. [Google Scholar] [CrossRef] [PubMed]
- Gustafsson, F.; Gunnarsson, F. Positioning using time-difference of arrival measurements. In Proceedings of the International conference on Acoustic, Speech and Signal Processing, Hong Kong, China, 6–10 April 2003. [Google Scholar]
- Ahmad, M.; Xiang, L.; Yousefi, S.; Xing, L. Theorical detection threshold of the proton-acoustic range verification technique. Med. Phys. 2015, 42, 5735–5744. [Google Scholar] [CrossRef] [PubMed]
- Knapp, C.; Carter, G. The generalized correlation method for estimation of time delay. IEE Tran. Acoust. Speech Signal Process. 1976, 24, 320–327. [Google Scholar] [CrossRef]
- Felis, I. Tecnologías Acústicas para la Detección de Materia Oscura. Diseño y desarrollo de un detector Geyser. Ph.D. Thesis, Universidad Politécnica de Valencia, Valencia, Spain, 2017. [Google Scholar]
- Assmann, W.; Kellnberger, S.; Reinhardt, S.; Lehrack, S.; Edlich, A.; Thirolf, P.G.; Moser, M.; Dollinger, G.; Omar, M.; Ntziachristos, V.; et al. Ionoacoustic characterization of the proton Bragg peak with submillimeter accuracy. Med. Phys. 2015, 42, 567–574. [Google Scholar] [CrossRef] [PubMed]
- Jones, K.C.; Segnal, C.M.; Avery, S. How proton pulse characteristics influence protoacoustic determination of proton-beam range: Simulation studies. Phys. Med. Biol. 2016, 61, 2213–2242. [Google Scholar] [CrossRef] [PubMed]
- Jones, K.C.; Witztum, A.; Sehgal, C.M.; Avery, S. Proton beam characterization by proton-induced acoustic emission: Simulation studies. Phys. Med. Biol. 2014, 59, 6549–6563. [Google Scholar] [CrossRef] [PubMed]

| Axis | Sensors | Source (mm) | |||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 1 | 2 | 3 | |
| X | H/2 | 0.0 | H/2 | H | 150 | 100 | 80 |
| Y | 0.0 | H/2 | H | H/2 | 150 | 180 | 100 |
| Z | 3H/4 | H/2 | H/2 | H/4 | 150 | 150 | 180 |
| Real Position (mm) | 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|
| X | 100 | 100.10 ± 0.11 | 100.10 ± 0.10 | 100.10 ± 0.10 | 94.00 ± 0.42 | 100.0 ± 0.01 |
| Y | 100 | 100.10 ± 0.10 | 98.00 ± 0.14 | 100.10 ± 0.11 | 96.00 ± 0.28 | 100.0 ± 0.01 |
| Z | 100 | 100.10 ± 0.10 | 96.00 ± 0.28 | 101.20 ± 0.14 | 94.00 ± 0.42 | 100.0 ± 0.01 |
| X | 100 | 100.00 ± 0.01 | 100.0 ± 0.01 | 100.0 ± 0.01 | 100.0 ± 0.01 | 102.0 ± 1.4 |
| Y | 180 | 100.20 ± 0.56 | 100.20 ± 0.56 | 181.2 ± 1.4 | 150 ± 21 | 163 ± 12 |
| Z | 150 | 100.10 ± 0.32 | 100.1 ± 00.35 | 147.4 ± 1.8 | 146 ± 21 | 145.8 ± 3.0 |
| X | 80 | 80.00 ± 0.01 | 78.0 ± 1.4 | 85.0 ± 4.5 | 71.0 ± 8.0 | 87.0 ± 4.9 |
| Y | 100 | 100.00 ± 0.01 | 98.0 ± 2.2 | 106.0 ± 5.2 | 93.0 ± 6.4 | 105.0 ± 3.5 |
| Z | 180 | 180.10 ± 0.10 | 178.0 ± 1.4 | 186.0 ± 5.3 | 168 ± 12 | 189.0 ± 6.4 |
| Axis | Sensors (mm) | Source (mm) | ||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 1 | 2 | |
| X | 600 | 500 | 400 | 500 | 410 | 450 |
| Y | 550 | 450 | 540 | 650 | 450 | 540 |
| Z | 380 | 280 | 340 | 340 | 350 | 330 |
| Axis | Real Position (mm) | Sine 100kHz | Sine 150kHz | Sweep Signal |
|---|---|---|---|---|
| X | 450 | 459.0 ± 9.0 | 460.0 ± 9.3 | 460.0 ± 9.2 |
| Y | 540 | 540.00 ± 0.72 | 540.00 ± 0.55 | 540.00 ± 0.43 |
| Z | 330 | 340.0 ± 9.2 | 330.00 ± 0.18 | 330.00 ± 0.32 |
| X | 410 | 401.0 ± 8.9 | 416.0 ± 5.7 | 418.0 ± 7.0 |
| Y | 450 | 448.0 ± 1.3 | 450.00 ± 0.44 | 450.00 ± 0.56 |
| Z | 350 | 352.0 ± 1.8 | 350.00 ± 0.36 | 350.00 ± 0.65 |
| Axis | Real Position (mm) | Sine 100 kHz |
|---|---|---|
| X | 450 | 459.0 ± 8.8 |
| Y | 540 | 540.00 ± 0.52 |
| Z | 330 | 330.00 ± 0.12 |
| X | 410 | 414.0 ± 3.3 |
| Y | 450 | 450.00 ± 0.52 |
| Z | 350 | 350.00 ± 0.49 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Otero, J.; Ardid, M.; Felis, I.; Herrero, A. Acoustic Location of Bragg Peak for Hadrontherapy Monitoring. Proceedings 2019, 4, 6. https://doi.org/10.3390/ecsa-5-05747
Otero J, Ardid M, Felis I, Herrero A. Acoustic Location of Bragg Peak for Hadrontherapy Monitoring. Proceedings. 2019; 4(1):6. https://doi.org/10.3390/ecsa-5-05747
Chicago/Turabian StyleOtero, Jorge, Miguel Ardid, Ivan Felis, and Alicia Herrero. 2019. "Acoustic Location of Bragg Peak for Hadrontherapy Monitoring" Proceedings 4, no. 1: 6. https://doi.org/10.3390/ecsa-5-05747
APA StyleOtero, J., Ardid, M., Felis, I., & Herrero, A. (2019). Acoustic Location of Bragg Peak for Hadrontherapy Monitoring. Proceedings, 4(1), 6. https://doi.org/10.3390/ecsa-5-05747







