A Novel Stress Tensor-Based Failure Criterion for Peridynamics †
Abstract
:1. Introduction
2. Overview of State-Based Peridynamics
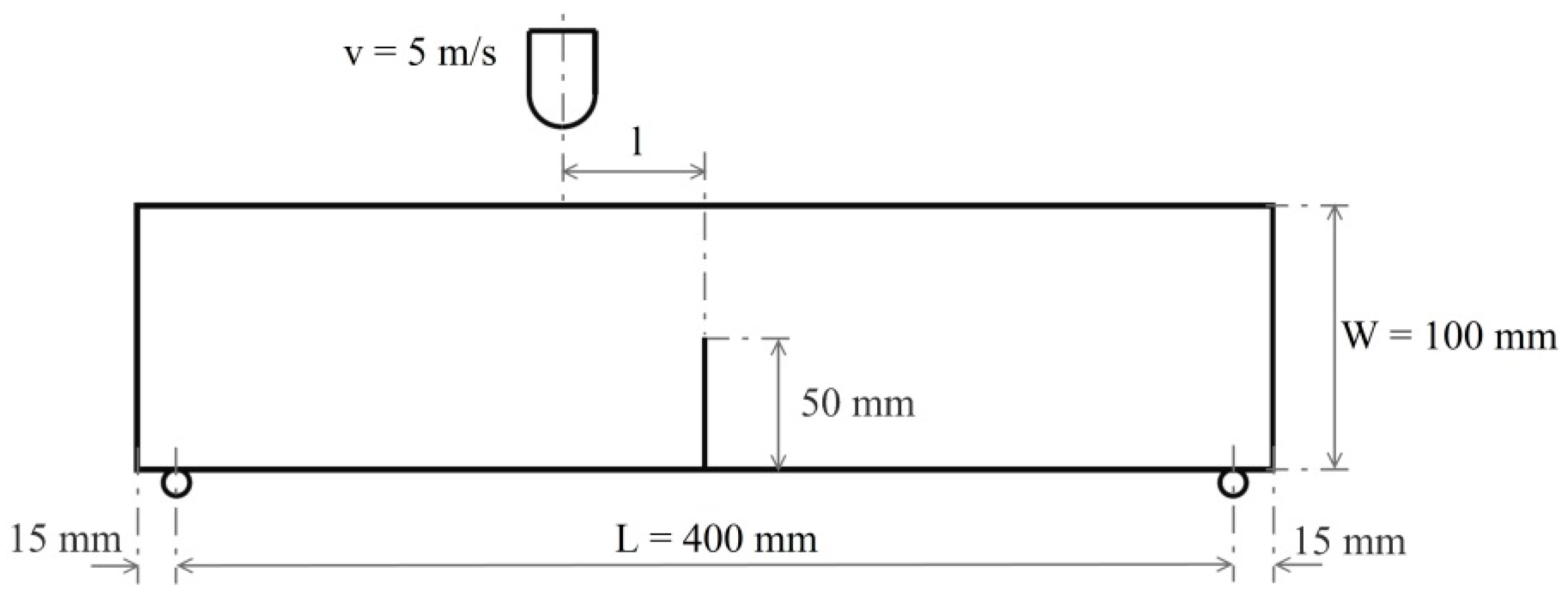
3. Method of Failure Criterion
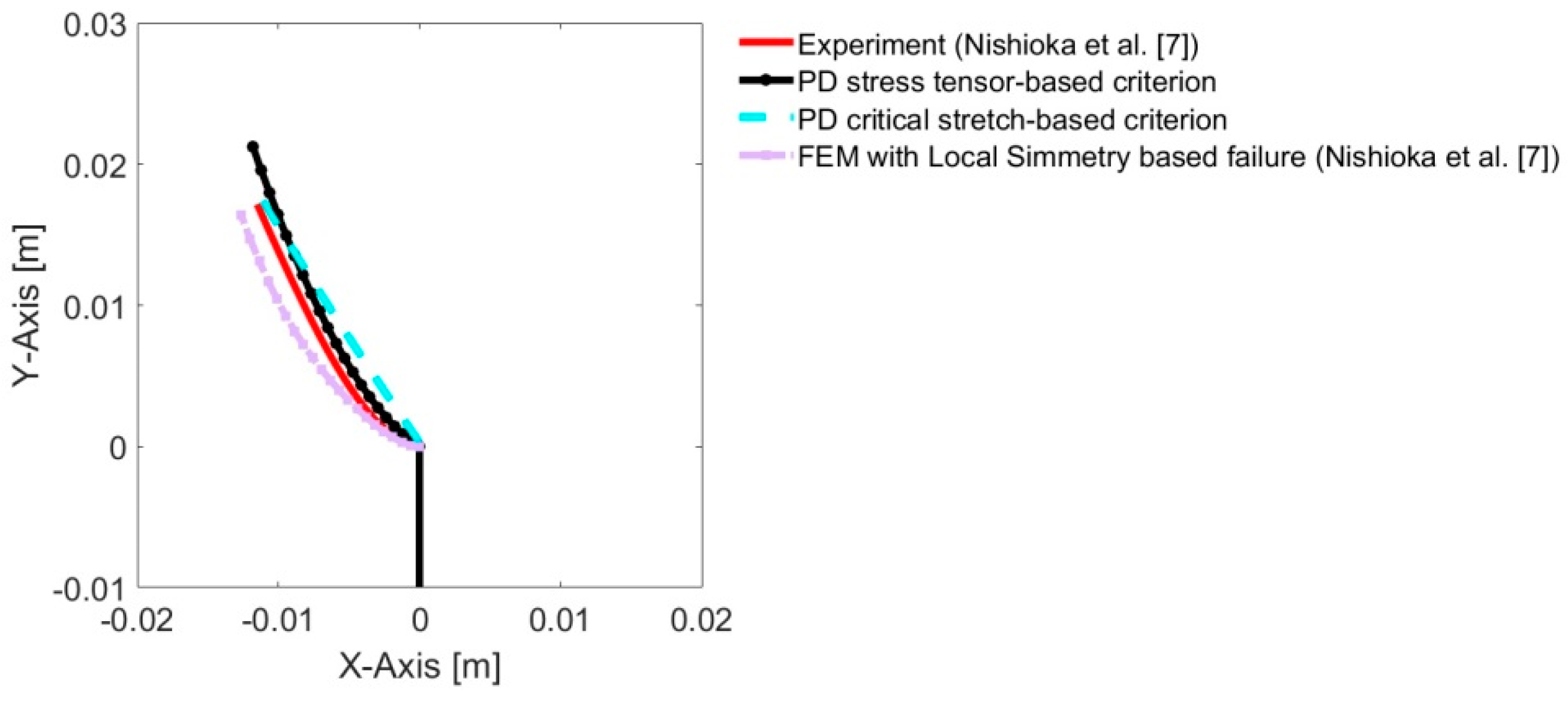
4. Results
5. Conclusions
References
- Silling, S.A.; Lehoucq, R. Peridynamic theory of solid mechanics. Adv. Appl. Mech. 2010, 44, 73–166. [Google Scholar]
- Rabczuk, T. Computational Methods for Fracture in Brittle and Quasi-Brittle Solids: State-of-the-Art Review and Future Perspectives. Appl. Math. 2012, 2013. [Google Scholar] [CrossRef]
- Dipasquale, D.; Zaccariotto, M.; Galvanetto, U. Crack propagation with adaptive grid refinement in 2D peridynamics. Int. J. Fract. 2014, 190, 1–22. [Google Scholar] [CrossRef]
- Oterkus, E.; Guven, I.; Madenci, E. Impact damage assessment by using peridynamic theory. Cent. Eur. J. Eng. 2012, 2, 523–531. [Google Scholar] [CrossRef]
- Silling, S.A.; Askari, E. A meshfree method based on the peridynamic model of solid mechanics. Comp. Struct. 2005, 83, 1526–1535. [Google Scholar] [CrossRef]
- Warren, T.L.; Silling, S.A.; Askari, A.; Weckner, O.; Epton, M.A.; Xu, J. A nonordinary state-based peridynamic method to model solid material deformation and fracture. Int. J. Solids Struct. 2009, 46, 1186–1195. [Google Scholar] [CrossRef]
- Nishioka, T.; Tokudome, H.; Kinoshita, M. Dynamic fracture-path prediction in impact fracture phenomena using moving finite element method based on delaunay automatic mesh generation. Int. J. Solids Struct. 2001, 38, 5273–5301. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dipasquale, D.; Shojaei, A.; Yooyen, S. A Novel Stress Tensor-Based Failure Criterion for Peridynamics. Proceedings 2019, 39, 23. https://doi.org/10.3390/proceedings2019039023
Dipasquale D, Shojaei A, Yooyen S. A Novel Stress Tensor-Based Failure Criterion for Peridynamics. Proceedings. 2019; 39(1):23. https://doi.org/10.3390/proceedings2019039023
Chicago/Turabian StyleDipasquale, Daniele, Arman Shojaei, and Soemsak Yooyen. 2019. "A Novel Stress Tensor-Based Failure Criterion for Peridynamics" Proceedings 39, no. 1: 23. https://doi.org/10.3390/proceedings2019039023
APA StyleDipasquale, D., Shojaei, A., & Yooyen, S. (2019). A Novel Stress Tensor-Based Failure Criterion for Peridynamics. Proceedings, 39(1), 23. https://doi.org/10.3390/proceedings2019039023




