Reinforcement of Pavements with Geosynthetics Estimation of Effective Elastic Properties ^†

Abstract

Composite materials are design to be able to achieve properties that would be unreachable if materials were used separately. A clear example of this, in civil engineering, is reinforced concrete. It is also important in this sense and into this field of work the material it is analyzed in this article, reinforced pavement of roads. The aim of this paper is to estimate the elastic properties of these materials. To reach that goal homogenization theory and related techniques would be used. The results obtained within this work shows significant structural benefits when including in the pavement these types of materials.

1. Introduction

A composite material can be defined as a material that is built like the mixture of different materials and one of them is on solid-phase, and it is designed to optimize the properties of the combined material. The aim of this union is, hence forth, the design of a material which properties cannot be reached by any of its components separately.

When studying properties of composite materials, it is usual to talk about the matrix of the material and the reinforcing materials such as fibers or aggregations, also called phases. The matrix is the material that includes the phases; inside of the matrix the phases are protected against adverse environmental or physics conditions which could damage them. This condition allows that the transference of different properties such as tensile stress can be developed without problem into the composite material. At the same time, it gives support to the reinforcing materials to avoid its sag when compressive stress takes place.

The most usual example of a composite material used in civil engineering is the reinforced concrete as mentioned above. This material improves the strength of a conventional concrete to compression, bending and tensile stresses. The composite material that is studied in this work is the reinforced pavement. Since the 80’s decade, reinforced pavements with geosynthetics materials are being used in civil engineering works, see [1], their principal tasks were orientated to drainage, segregation, filter or mainly reinforce functions. When talking about reinforcement it is focused on tensile and torsional stress.

The geosynthetic material used for reinforced pavements represent an example of laminated compound. On behalf of the orientation of the fibers that form the layers of the geosynthetic material the strength of the composite material can be improved. In this sense, although the experience shows the evidences of using geosynthetics for the reinforcement of other materials creating composite materials with better characteristics. In that sense, While the advantages of using geosynthetic reinforcements are unquestionable, the scientific mechanisms to quantify this reinforcement are unclear and object of recent research by different authors [2,3,4,5].

The objective of this work is to estimate elastic properties in pavement reinforced with geosynthetic, applying techniques related to the Theory of Homogenization.

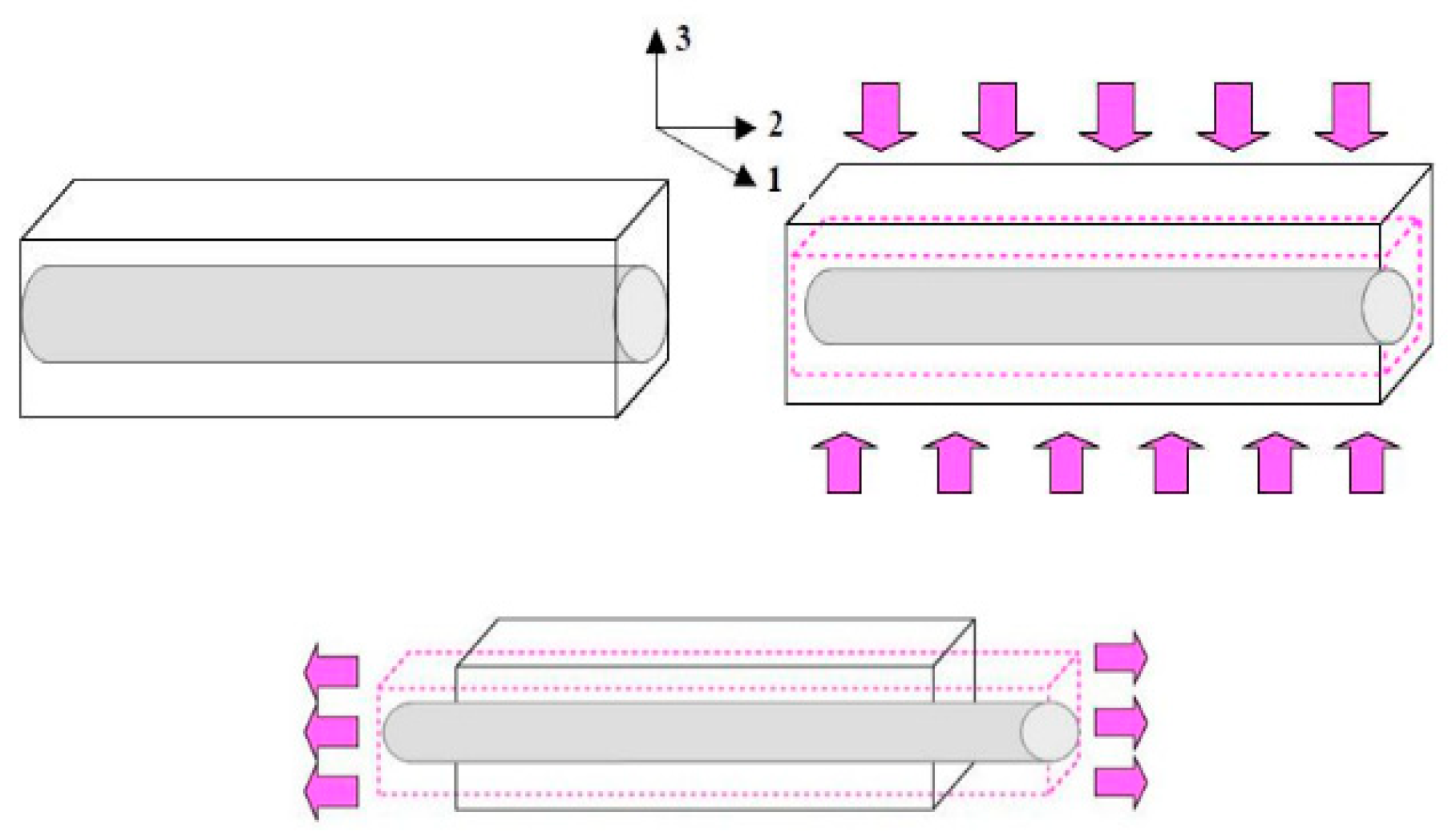
2. Materials and Methods

Tensor deformation (ε) components has been related with the tensor tensions (σ) through the generalized Hooke’s law, as follows:

$$\sigma =C\epsilon ,$$

(1)

Then, the constitutive equations of an elastic solid can be expressed through the following symmetric matrix:

$$\left(\begin{array}{c}{\sigma }_{11}\\ {\sigma }_{22}\\ {\sigma }_{33}\\ {\tau }_{23}\\ {\tau }_{13}\\ {\tau }_{12}\end{array}\right)=\left(\begin{array}{cccccc}{C}_{11}& C_{12}& C_{13}& C_{14}& C_{15}& C_{16}\\ C_{21}& C_{22}& C_{23}& C_{24}& C_{25}& C_{26}\\ C_{31}& C_{32}& C_{33}& C_{34}& C_{35}& C_{36}\\ C_{41}& C_{42}& C_{43}& C_{44}& C_{45}& C_{46}\\ C_{51}& C_{52}& C_{53}& C_{54}& C_{55}& C_{56}\\ C_{61}& C_{62}& C_{63}& C_{64}& C_{65}& C_{66}\end{array}\right)\left(\begin{array}{c}{\epsilon }_{11}\\ {\epsilon }_{22}\\ {\epsilon }_{33}\\ {\gamma }_{23}\\ {\gamma }_{13}\\ {\gamma }_{12}\end{array}\right)$$

(2)

The inverse of the stiffness matrix C is called the flexibility matrix and is denoted by S, satisfying:

$$\epsilon =S\sigma ,$$

(3)

When the material has three orthogonal planes with elastic symmetry and in one of the planes the behaviour is isotropic, the material is said to be transversely isotropic. In this case the number of elastic constants is reduced to 5:

$$C_{T.Isotropic}=\left(\begin{array}{cccccc}{C}_{11}& C_{12}& C_{13}& 0& 0& 0\\ C_{12}& C_{11}& C_{13}& 0& 0& 0\\ C_{13}& C_{13}& C_{33}& 0& 0& 0\\ 0& 0& 0& C_{44}& 0& 0\\ 0& 0& 0& 0& C_{44}& 0\\ 0& 0& 0& 0& 0& \frac{C_{11}-C_{12}}{2}\end{array}\right)$$

(4)

Knowing the mechanical properties of the different materials separately, their respective volume fractions and following the Theory of Homogenization, the effective properties of the composite material have been obtained. Specifically, the Mixtures Law has been used, also called Voigt-Reuss [6,7] or Wiener bounds [8] considerate as one of the simplest homogenization techniques.

This Law establishes conditions of isodeformation and isotension in the composite material, where a representative cell submitted to these hypotheses would be represented by Figure 1.

Starting from the previous hypotheses, elastic properties of the composite material can be estimated through the following expressions:

• Estimation of axial rigidity modules of composite material:

$$E_i^h=E_i^f{\varnothing }_f+E_i^m{\varnothing }_m$$

(5)

• Estimation of the transverse stiffness module

$$E_3^h=\frac{1}{\frac{{\varnothing }_f}{E_3^f}+\frac{{\varnothing }_m}{E_3^m}}$$

(6)

• Poisson modules and cutting of laminated material:

$$\begin{gathered} {\nu }_{12}^H={\nu }_{21}^H={\varnothing }_f{\nu }_{}^f+{\varnothing }_m{\nu }_{}^m \\ {\nu }_{23}^H={\nu }_{13}^H,{\nu }_{32}^H={\nu }_{31}^H,with{\nu }_{kl}^H=\frac{E_k}{2{\mu }_{kl}^H}-1 \end{gathered}$$

(7)

Using the properties of the homogenized material given by the Expressions (5)–(7) we can formulate Hooke’s Law (1) for reinforced pavement through:

$$C^H={\sigma }^H{\epsilon }^H$$

(8)

where $C^H$ is given by the Expression (9).

$$\left(\begin{array}{cccccc}{E}_1^H\frac{1-{\nu }_{23}^H{\nu }_{32}^H}{\mathsf{\Delta }}& E_1^H\frac{{\nu }_{21}^H-{\nu }_{31}^H{\nu }_{23}^H}{\mathsf{\Delta }}& E_1^H\frac{{\nu }_{31}^H-{\nu }_{21}^H{\nu }_{32}^H}{\mathsf{\Delta }}& 0& 0& 0\\ & E_1^H\frac{1-{\nu }_{23}^H{\nu }_{32}^H}{\mathsf{\Delta }}& E_1^H\frac{{\nu }_{31}^H-{\nu }_{21}^H{\nu }_{32}^H}{\mathsf{\Delta }}& 0& 0& 0\\ & & E_3^H\frac{1-{\nu }_{12}^H{\nu }_{21}^H}{\mathsf{\Delta }}& 0& 0& 0\\ & & & \frac{E_1^H}{2\left(1+{\nu }_{31}^H\right)}& 0& 0\\ & & & & \frac{E_1^H}{2\left(1+{\nu }_{31}^H\right)}& 0\\ sim& & & & & \frac{E_1^H\frac{1-{\nu }_{23}^H{\nu }_{32}^H}{\mathsf{\Delta }}-E_1^H\frac{{\nu }_{21}^H-{\nu }_{31}^H{\nu }_{23}^H}{\mathsf{\Delta }}}{2}\end{array}\right)$$

(9)

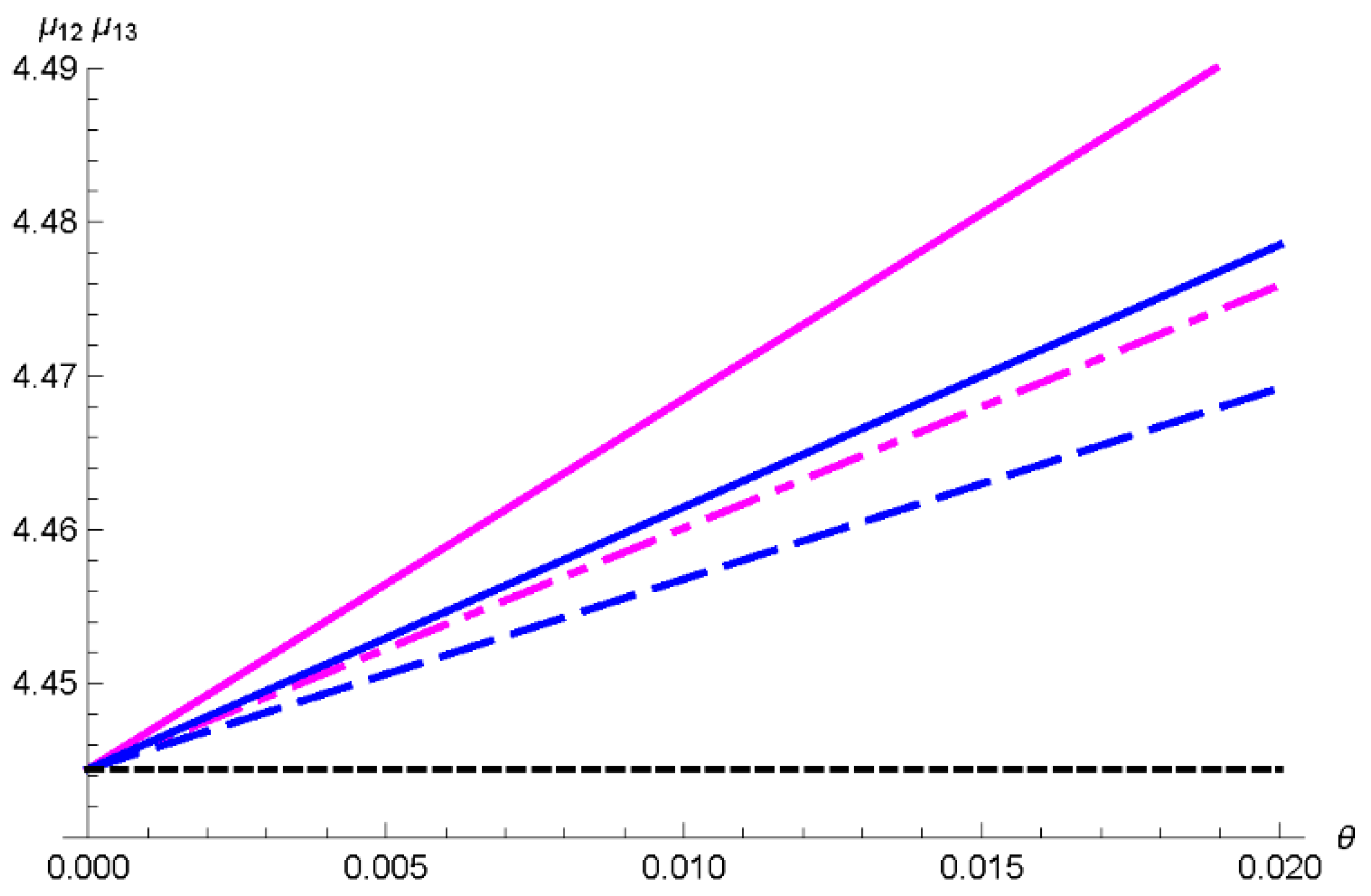
3. Results

The obtained results to validate the previous proposal can be seen in the Figure 2.

To implement the above formulation, we use some data empirically obtained in works by different authors [9,10] and implementing the previous estimates in the Mathematica numerical software [11]. Some numerical homogenized results can be showed below.

Upper and lower range of the stiffness and flexibility matrix for floors reinforced with 1% polypropylene:

$$\begin{array}{cc}\mathrm{Stiffness\; matrix} {\mathrm{C}}^{\mathrm{V}}& \mathrm{Stiffness\; matrix} {\mathrm{C}}^{\mathrm{R}}\\ \left(\begin{array}{cccccc}5.9580& 1.4895& 5.2132& 0& 0& 0\\ 1.4895& 5.9580& 4.4685& 0& 0& 0\\ 5.2132& 0& 9.6817& 0& 0& 0\\ 0& 0& 0& 4.4685& 0& 0\\ 0& 0& 0& 0& 4.4685& 0\\ 0& 0& 0& 0& 0& 4.4685\end{array}\right)& \left(\begin{array}{cccccc}5.9468& 1.4867& 5.2034& 0& 0& 0\\ 1.4867& 5.9468& 4.4601& 0& 0& 0\\ 5.2034& 0& 9.6635& 0& 0& 0\\ 0& 0& 0& 4.4601& 0& 0\\ 0& 0& 0& 0& 4.4601& 0\\ 0& 0& 0& 0& 0& 4.4602\end{array}\right)\\ \mathrm{Flexibility\; matrix} {\mathrm{S}}^{\mathrm{V}}& \mathrm{Flexibility\; matrix} {\mathrm{S}}^{\mathrm{R}}\\ \left(\begin{array}{cccccc}0.2958& -0.073& -0.125& 0& 0& 0\\ 0.0455& 0.1564& -0.096& 0& 0& 0\\ 0.159& 0.0398& 0.1706& 0& 0& 0\\ 0& 0& 0& 0.2237& 0& 0\\ 0& 0& 0& 0& 0.2237& 0\\ 0& 0& 0& 0& 0& 0.2237\end{array}\right)& \left(\begin{array}{cccccc}0.2964& -0.074& -0.125& 0& 0& 0\\ 0.0456& 0.1567& -0.096& 0& 0& 0\\ -0.159& 0.0399& 0.1710& 0& 0& 0\\ 0& 0& 0& 0.2242& 0& 0\\ 0& 0& 0& 0& 0.2242& 0\\ 0& 0& 0& 0& 0& 0.2242\end{array}\right)\end{array}$$

4. Conclusions

As seen in Figure 2, the use of geosynthetics as pavement reinforcement provides significant structural benefits. The results obtained confirm the conclusions, which using several analytical and empirical methods suggest several authors [12,13]. In particular, the presence of reinforcements with geosynthetics makes the resulting composite material (reinforced pavement) more resistant and at the same time more ductile (due to the properties of the reinforcement). In particular, it improves the tensile strength and axial and tangential compression.