Bayesian Identification of Dynamical Systems †
Abstract
:1. Introduction
2. Theoretical Foundations
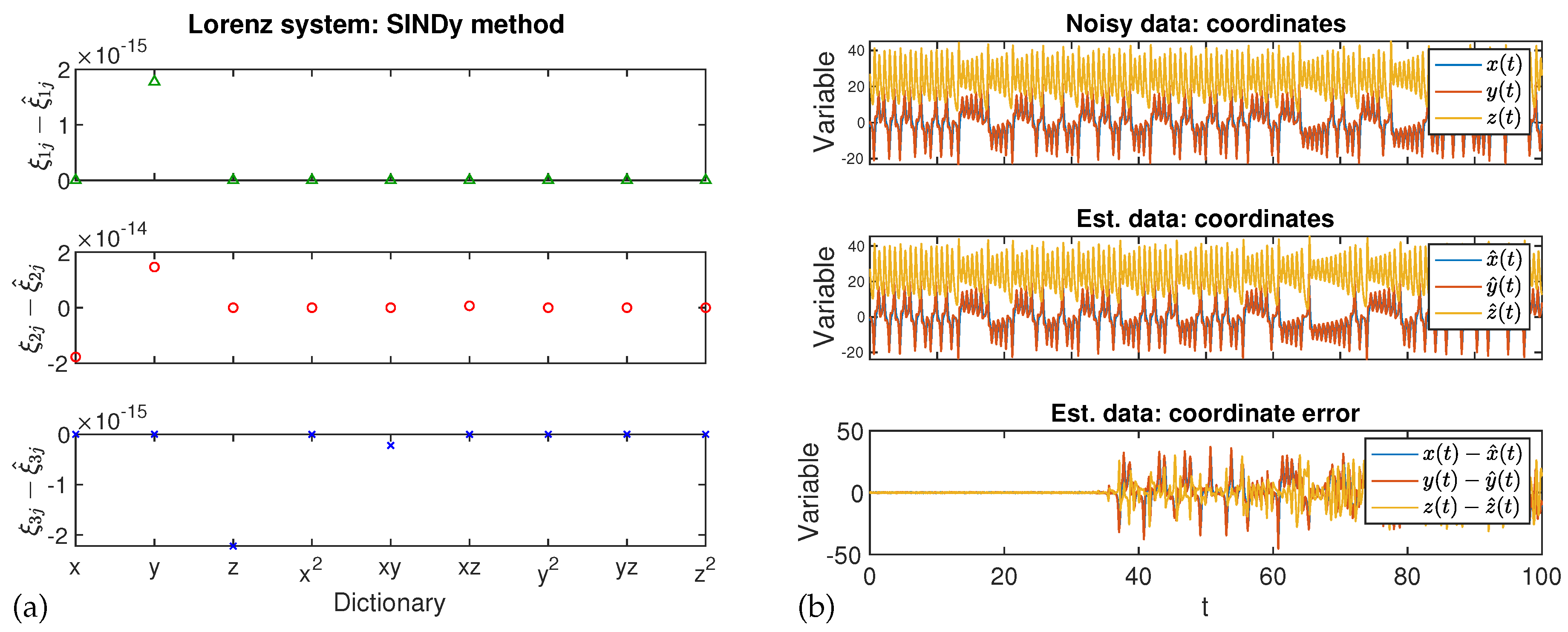
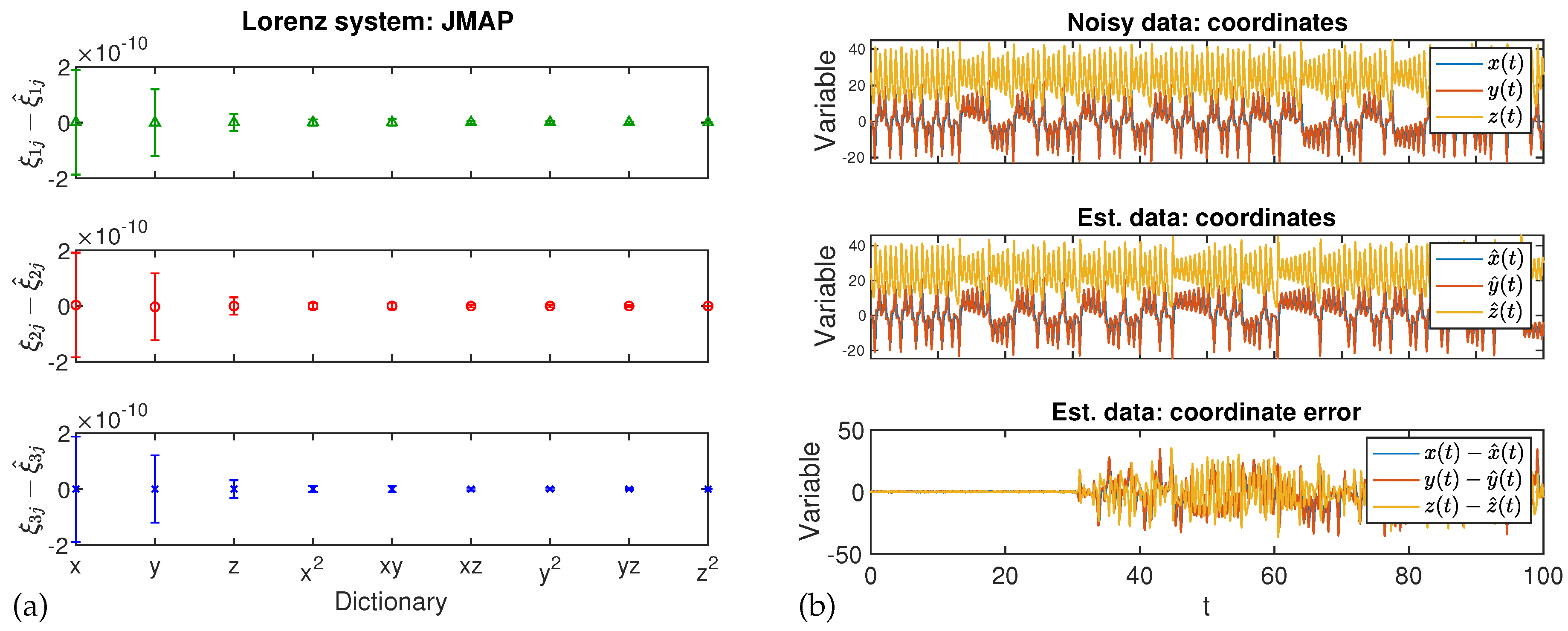
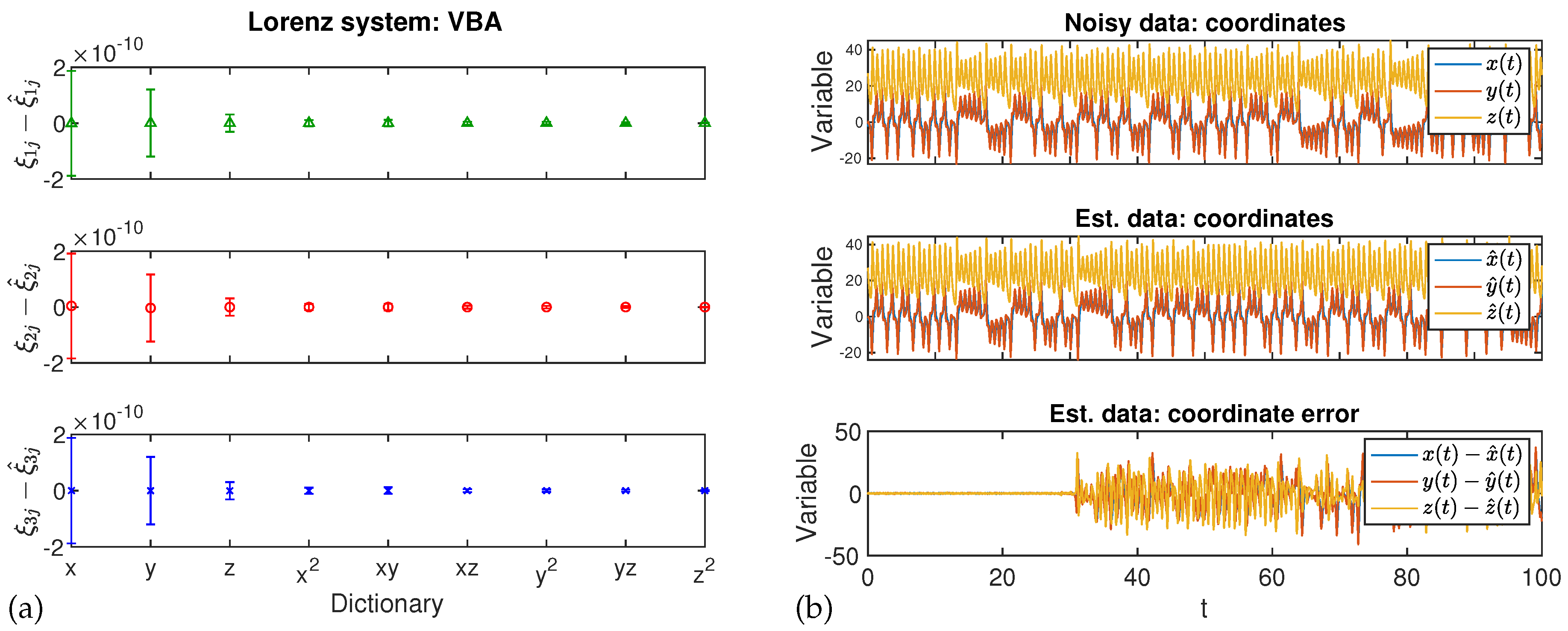
3. Application
4. Results
5. Conclusions
Funding
Conflicts of Interest
References
- Brunton, S.L.; Proctor, J.L.; Kutz, J.N. Discovering governing equations from data by sparse identification of nonlinear dynamical systems. Proc. Natl. Acad. Sci. 2016, 113, 3932–3937. [Google Scholar] [CrossRef] [PubMed]
- Mangan, N.M.; Kutz, J.N.; Brunton, S.L.; Proctor, J.L. Model selection for dynamical systems via sparse regression and information criteria. Roy. Soc. Proc. A 2017, 473, 20170009. [Google Scholar] [CrossRef] [PubMed]
- Rudy, S.H.; Brunton, S.L.; Proctor, J.L.; Kutz, J.N. Data-driven discovery of partial differential equations. Sci. Adv. 2017, 3, e1602614. [Google Scholar] [CrossRef] [PubMed]
- Tikhonov, A.N. Solution of incorrectly formulated problems and the regularization method. Dokl. Akad. Nauk SSSR 1963, 151, 501–504. (In Russian) [Google Scholar]
- Santosa, F.; Symes, W.W. Linear inversion of band-limited reflection seismograms. SIAM J. Sci. Stat. Comp. 1986, 7, 1307–1330. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression shrinkage and selection via the Lasso. J. R. Stat. Soc. B 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Zhang, L.; Schaeffer, H. On the convergence of the SINDy algorithm. arXiv 2018, arXiv:1805.06445v1. [Google Scholar] [CrossRef]
- Brunton, S.L.; Brunton, B.W.; Proctor, J.L.; Kaiser, E.; Kutz, J.N. Koopman invariant subspaces and finite linear representations of nonlinear dynamical systems for control. PLoS ONE 2016, 11, e0150171. [Google Scholar] [CrossRef] [PubMed]
- Brunton, S.L.; Brunton, B.W.; Proctor, J.L.; Kaiser, E.; Kutz, J.N. Chaos as an intermittently forced linear system. Nat. Comm. 2017, 8, 19. [Google Scholar] [CrossRef] [PubMed]
- Taira, K.; Brunton, S.L.; Dawson, S.T.M.; Rowley, C.W.; Colonius, T.; McKeon, B.J.; Schmidt, O.T.; Gordeyev, S.; Theofilis, V.; Ukeiley, L.S. Modal analysis of fluid flows: An overview. AIAA J. 2017, 55, 4013–4041. [Google Scholar] [CrossRef]
- Mohammad-Djafari, A. Inverse problems in signal and image processing and Bayesian inference framework: From basic to advanced Bayesian computation. In Proceedings of the Scube Seminar, L2S, CentraleSupelec, At Gif-sur-Yvette, France., 27 March 2015. [Google Scholar]
- Mohammad-Djafari, A. Approximate Bayesian computation for big data. In Proceedings of the Tutorial at MaxEnt 2016, Ghent, Belgium, 10–15 July 2016. [Google Scholar]
- Teckentrup, A. Introduction to the Bayesian approach to inverse problems. In Proceedings of the MaxEnt 2018, Alan Turing Institute, UK, 6 July 2018. [Google Scholar]
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niven, R.K.; Mohammad-Djafari, A.; Cordier, L.; Abel, M.; Quade, M. Bayesian Identification of Dynamical Systems. Proceedings 2019, 33, 33. https://doi.org/10.3390/proceedings2019033033
Niven RK, Mohammad-Djafari A, Cordier L, Abel M, Quade M. Bayesian Identification of Dynamical Systems. Proceedings. 2019; 33(1):33. https://doi.org/10.3390/proceedings2019033033
Chicago/Turabian StyleNiven, Robert K., Ali Mohammad-Djafari, Laurent Cordier, Markus Abel, and Markus Quade. 2019. "Bayesian Identification of Dynamical Systems" Proceedings 33, no. 1: 33. https://doi.org/10.3390/proceedings2019033033
APA StyleNiven, R. K., Mohammad-Djafari, A., Cordier, L., Abel, M., & Quade, M. (2019). Bayesian Identification of Dynamical Systems. Proceedings, 33(1), 33. https://doi.org/10.3390/proceedings2019033033






