Effects of Neuronal Noise on Neural Communication ^†

Abstract

In this work, we propose an approach to better understand the effects of neuronal noise on neural communication systems. Here, we extend the fundamental Hodgkin-Huxley (HH) model by adding synaptic couplings to represent the statistical dependencies among different neurons under the effect of additional noise. We estimate directional information-theoretic quantities, such as the Transfer Entropy (TE), to infer the couplings between neurons under the effect of different noise levels. Based on our computational simulations, we demonstrate that these nonlinear systems can behave beyond our predictions and TE is an ideal tool to extract such dependencies from data.

1. Introduction

Mathematical models and analysis have been a strong tool to answer many important questions in biology and the work of Hodgkin and Huxley on nerve conduction is one of the best examples of it [1]. In 1952, after many years of theoretical and experimental work of physiologists, a mathematical model was proposed by HH to explain the action potential generation of neurons using conductance models that are defined for different electrically excitable cells [2,3,4]. Despite the rapid growth in the number of analyses on the communication between neurons, the noise effect has generally been overlooked in the literature. Recently, neuronal noise effects have started to be incorporated into the models, due to a phenomenon, called “Stochastic Resonance” [5]. The communication between neurons is maintained by electrical signals, called ‘’Action Potentials (AP)”. If the action potentials, as a response to a stimulant, exceeds a certain threshold value, these signals are referred to as “Spikes”. The existence of a spike is determined by the value of a threshold value and additional noise component can easily increase or decrease the value of an AP versus the threshold, thus change the neural spike train code. Therefore, the noise is not merely a nuisance factor and it is capable of changing the meaning of the “neuronal code”. For this reason, to better understand how these changes can occur in a very complex system, such as our brain, we must first understand the underlying working principles of neuronal noise, which sets the framework of our investigations.

Here, we utilize information theory to better understand the effects of neuronal noise on the overall communication. Therefore, we generalize the HH model in such a way that the noise can be added to the system beside the coupling among the neurons. In the literature, the effect of coupling among different neurons have been explored by using TE [6], however, to the best of our knowledge, the effects of noise on these interactions have not been fully considered yet.

On the other hand, certain types of models have been suggested to include the noise in the HH model [7] without any coupling between the neurons. Here, we approach the complicated modeling problem by using a simplified version including two neurons, coupling between them, and additional noise terms. We propose utilizing information theory to analyze the relationships in neural communication.

In the literature, information-theoretic quantities, such as Entropy, Mutual Information (MI) and Transfer Entropy (TE) have been successfully utilized to analyze the statistical dependencies and relationships between random variables of highly complex systems [8]. Among these, MI is a symmetric quantity reporting the dependency between two variables, whereas TE, is an asymmetric quantity that can be used to infer the direction of the interaction (as affecting and affected variables) between them [9]. All the above quantities are calculated from observational data by inferring probability distributions. Despite the wide variety of different distribution estimation techniques, the whole procedure still suffers from adverse effects, such as the bias. Most common techniques in probability distribution estimation involve histograms [10], Parzen windows [11] and adaptive methods [12]. In the literature, histogram estimation is widely used due to its computational simplicity. To rely on estimations from data, reporting the statistical significance of each estimate [13] constitutes an important part of the methods.

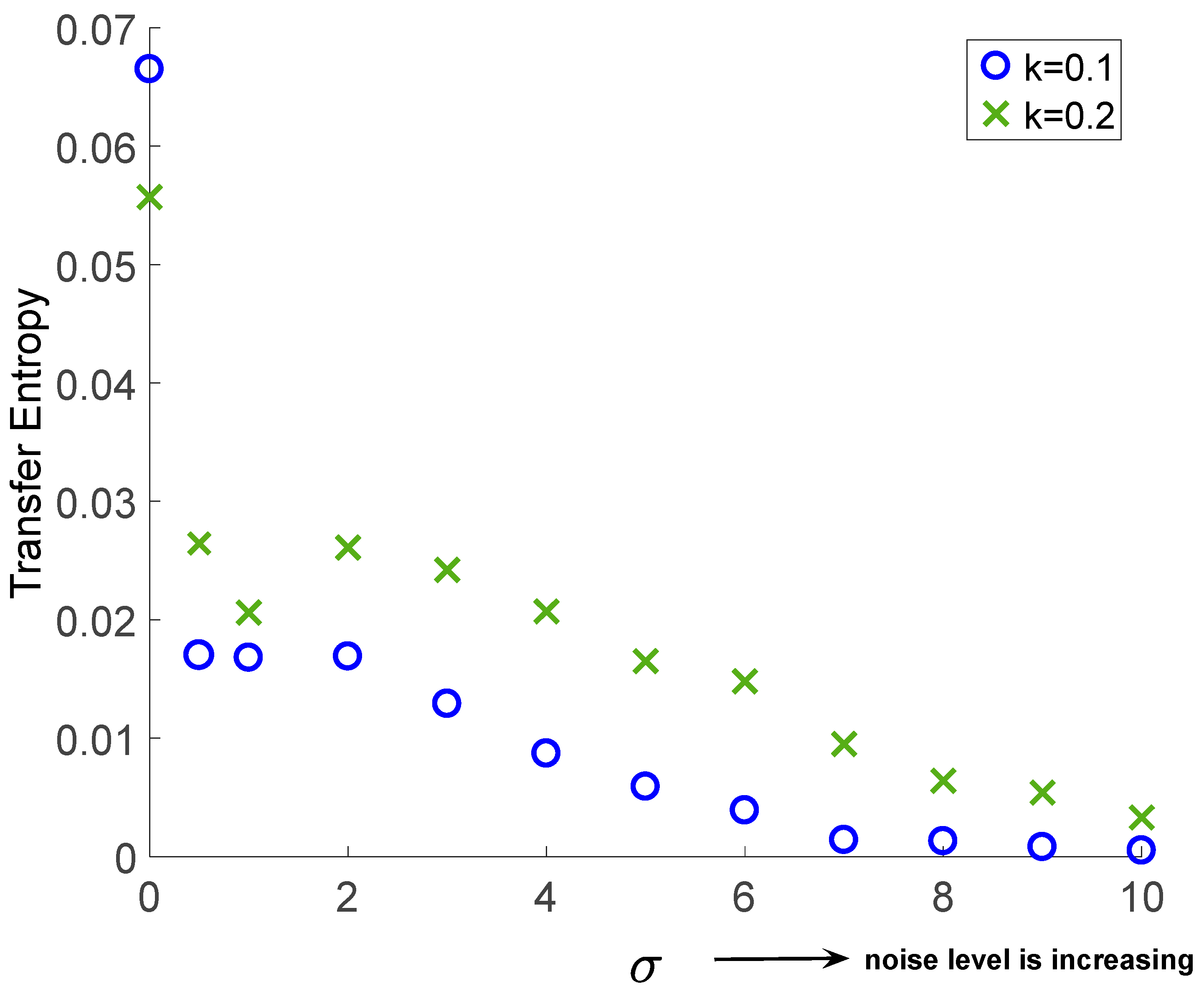
In this work, we propose utilizing TE to investigate the directional relationships between the coupled neurons of a HH model under noisy conditions. Therefore, we extend the traditional HH model and analyzed the effect of noise on the directional relationships between the coupled neurons. As our first approach to model noisy neuronal interaction, we demonstrate the effect under certain levels of noise power in the simulations. Based on these simulations, we observe that the original interactions are preserved despite many changes in the structure of the neuronal code structure. Our future work will be based on the generalization of this modeling to consider N neurons and the effect of noise on their interactions.

2. Materials and Methods

2.1. The Hodgkin-Huxley Model

In this study we use Hodgkin-Huxley model which mimics the spiking behavior of the neurons recorded from the squid giant axon. This is the first mathematical model describing the action potential generation and it is one of the major breakthroughs of computational neuroscience [1]. In 1952 two physiologists Hodgkin and Huxley got the Nobel prize after this work and after their work Hodgkin-Huxley type models are defined for many different electrically excitable cells such as cardiomyocytes [2], pancreatic beta cells [3] and hormone secretion [4]. They observed that cell membranes behave much like electrical circuits. The basic circuit elements are the phospholipid bilayer of the cell, which behaves like a capacitor that accumulates ionic charge while the electrical potential across the membrane changes. Moreover, resistors in a circuit are analogue to the ionic permeabilities of the membrane and the electrochemical driving forces are analogous to batteries driving the ionic currents. Na⁺, K⁺, Ca²⁺ and Cl⁻ ions are responsible for almost all the electrical actions in the body. Thus, the electrical behavior of cells is based upon the transfer and storage of ions and Hodgkin and Huxley observed that K⁺ and Na⁺ ions are mainly responsible for the HH system.

Mathematical description of the Hodgkin-Huxley model starts with the membrane potential V based on the conservation of electric charge defined as follows

$$C_m\frac{dV}{dt}=I_{ion}+I_{app}$$

(1)

where $C_m$ is the membrane capacitance, $I_{app}$ is the applied current and $I_{ion}$ represents the sum of individual ionic currents and modeled according to Ohm’s Law:

$$I_{ion}=-g_K\left(\mathrm{V}-V_K\right)-g_{Na}\left(\mathrm{V}-V_{Na}\right)-g_L\left(\mathrm{V}-V_L\right).$$

(2)

here $g_K$, $g_{Na}$ and $g_L$ are conductances, $V_{Na}$,$V_K$,$V_L$ are the reversal potentials associated with the currents. Hodgkin and Huxley observed that conductances are also voltage dependent. They realize that $g_K$ depends on four activation gates and defined as $g_K=\overline{g_K}{n}^4$ whereas $g_{Na}$ depends on three activation gates and one inactivation gate and modeled as $g_{Na}=\overline{g_{Na}}{m}^{3}h$. In the HH model, ionic currents are defined as:

$$I_{Na}=\overline{g_{Na}}{m}^{3}h\left(\mathrm{V}-V_{Na}\right)$$

(3)

$$I_K=\overline{g_K}{n}^4\left(\mathrm{V}-V_K\right)$$

(4)

$$I_L=\overline{g_L}\left(\mathrm{V}-V_L\right)$$

(5)

with Na⁺ activation variable m and inactivation variable h, and K⁺ activation variable n. Here $(\stackrel{-}{.})$ denotes maximal conductances. Activation and inactivation dynamics of the channels are changing according to the differential equations below.

$$\frac{dm}{dt}=\frac{m_{\infty }\left(V_i\right)-m}{{\tau }_m\left(V_i\right)}$$

(6)

$$\frac{dh}{dt}=\frac{h_{\infty }\left(V_i\right)-h}{{\tau }_h\left(V_i\right)}$$

(7)

$$\frac{dn}{dt}=\frac{n_{\infty }\left(V_i\right)-n}{{\tau }_n\left(V_i\right)}$$

(8)

The steady state activation and inactivation functions together with time constants are defined as below and the transition rates ${\alpha }_x \mathrm{a}\mathrm{n}\mathrm{d} {\beta }_x$ are given in

Table 1. Transition rates and parameter values for the HH Model.

Transition Rates (ms−1)	${\alpha }_m$	$0.1(40+V_i)/(1- \mathrm{e}\mathrm{x}\mathrm{p}(-(55+V_i)/10)$
	${\beta }_m$	$4 \exp (-(65+V_i)/18)$
	${\alpha }_h$	$0.07 \exp (-(65+V_i)/20)$
	${\beta }_h$	$1/(1+\mathrm{e}\mathrm{x}\mathrm{p}(-\left(35+V_i\right))$
	${\alpha }_n$	$0.01 (55+V_i)/(1-\mathrm{e}\mathrm{x}\mathrm{p}(-(10+55))$
	${\beta }_n$	$0.125 \exp (-(V_i+65)/80)$
Parameter Values	$C_m$	$1 \mu F$
	$I_{app}$	$8 mA$
	$g_{Na}$	$120 \mu S$
	$g_K$	$36 \mu S$
	$g_L$	$0.3 \mu S$
	$V_{Na}$	$50 mV$
	$V_K$	$-77 mV$
	$V_L$	$-54.4 mV$

.

$$x_{\infty }\left(V_i\right)=\frac{{\alpha }_x\left(V_i\right)}{{\alpha }_x\left(V\right)+{\beta }_x\left(V\right)}$$

(9)

$${\tau }_x\left(V_i\right)=\frac{1}{{\alpha }_x\left(V_i\right)+{\beta }_x\left(V_i\right)},x=m,h,n$$

(10)

2.2. Information Theoretic Quantities

In information theory, Shannon entropy is defined to be the average uncertainty for finding the system at a particular state ‘x’ out of a possible set of states ‘X’, where p(x) denotes the probability of that state. Also, it is used to quantify the amount of information needed to describe a dataset. Shannon entropy is given by the following formula

$$H\left(X\right)=-\sum _{x\in X}p\left(x\right)log\left(p\left(x\right)\right)$$

(11)

Mutual information (MI), is another fundamental information-theoretic quantity which is used to quantify the information shared between two datasets. Given two datasets denoted by X and Y, the MI can be written as follows:

$$MI\left(X,Y\right)=\sum _{x\in X}\sum _{y\in Y}p\left(x,y\right)log\frac{p\left(x,y\right)}{p\left(x\right)p\left(y\right)}$$

(11)

The MI is a symmetric quantity and it can be rewritten as a sum and difference of Shannon entropies by

$$MI\left(X,Y\right)=H\left(X\right)+H\left(Y\right)-H(X,Y)$$

(12)

where $H(X,Y)$ is the joint Shannon entropy. If there is a directional dependency between the variables, such as a cause and effect relationship, a symmetric measure cannot unveil the dependency information from data. In the literature, TE was proposed to analyze the directional dependencies between two Markov processes. To quantify the directional effect of a variable X on Y, the TE is defined by the conditional distribution of Y depending on the past samples of both processes versus the conditional distribution of that variable depending only on its own past values [14]. Thus, the asymmetry of TE helps us detect two directions of information flow. The TE definition in both directions (between variables X and Y) are given by the following equations:

$${TE}_{XY}=T\left(Y_{i+1}|{\mathbf{Y}}_i^{(k)},{\mathbf{X}}_i^{(l)}\right)=\sum _{y_{i+1},{\mathbf{y}}_i^{(k)},{\mathbf{x}}_i^{(l)}}p\left(y_{i+1},{\mathbf{y}}_i^{(k)},{\mathbf{x}}_i^{(l)}\right){\mathrm{l}\mathrm{o}\mathrm{g}}_2\frac{p\left(y_{i+1}|{\mathbf{y}}_i^{(k)},{\mathbf{x}}_i^{(l)}\right)}{p\left(y_{i+1}|{\mathbf{y}}_i^{(k)}\right)}$$

(13)

$${TE}_{YX}=T\left(X_{i+1}|{\mathbf{X}}_i^{(k)},{\mathbf{Y}}_i^{(l)}\right)=\sum _{x_{i+1},{\mathbf{x}}_i^{(k)},{\mathbf{y}}_i^{(l)}}p\left(x_{i+1},{\mathbf{x}}_i^{(k)},{\mathbf{y}}_i^{(l)}\right){\mathrm{l}\mathrm{o}\mathrm{g}}_2\frac{p\left(x_{i+1}|{\mathbf{x}}_i^{(k)},{\mathbf{y}}_i^{(l)}\right)}{p\left(x_{i+1}|{\mathbf{x}}_i^{(k)}\right)}$$

(14)

where ${\mathbf{x}}_i^{(k)}=\left\{x_i^{},\dots ,x_{i-k+1}^{}\right\}$ and ${\mathbf{y}}_i^{(l)}=\left\{y_i^{},\dots ,y_{i-l+1}^{}\right\}$ are past states, and X and Y are kth and lth order Markov processes, respectively, such that X depends on the k previous values and Y depends on the l previous values. In the literature, k and l are also known as the embedding dimensions.

All the above quantities involve estimation of probability distributions from the observed data. Among many approaches in the literature, we utilize the histogram-based method to estimate the distributions on (14) and (15), due to its computational simplicity. In order to assess the statistical significance of the TE estimations, surrogate data testing is applied, and the p-values are reported.

2.3. The Proposed Method

In this paper we focus on the system of two coupled HH neurons with synaptic coupling from neuron 1 to neuron 2. Also, current noise is added with normal distribution for the action potential generation of the squid axons for this two-neuron network. It involves a fast sodium current $I_{i,Na}$, a delayed rectifying potassium current $I_{i,K}$ and a leak current $I_{i,L}\left(\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{e}\mathrm{d} \mathrm{i}\mathrm{n} \frac{\mu A}{{cm}^2}\right) \mathrm{f}\mathrm{o}\mathrm{r} i=\mathrm{1,2}$. The differential equations for the rate of change of voltage for these neurons are given as follows,

$$C_m\frac{d{V}_1}{dt}=I_{i,app}-I_{i,Na}-I_{i,K}-I_{i,L}+N\left(0,\sigma \right),$$

(15)

$$C_m\frac{d{V}_2}{dt}=I_{i,app}-I_{i,Na}-I_{i,K}-I_{i,L}+k(V_2-V_1)+N\left(0,\sigma \right)$$

(16)

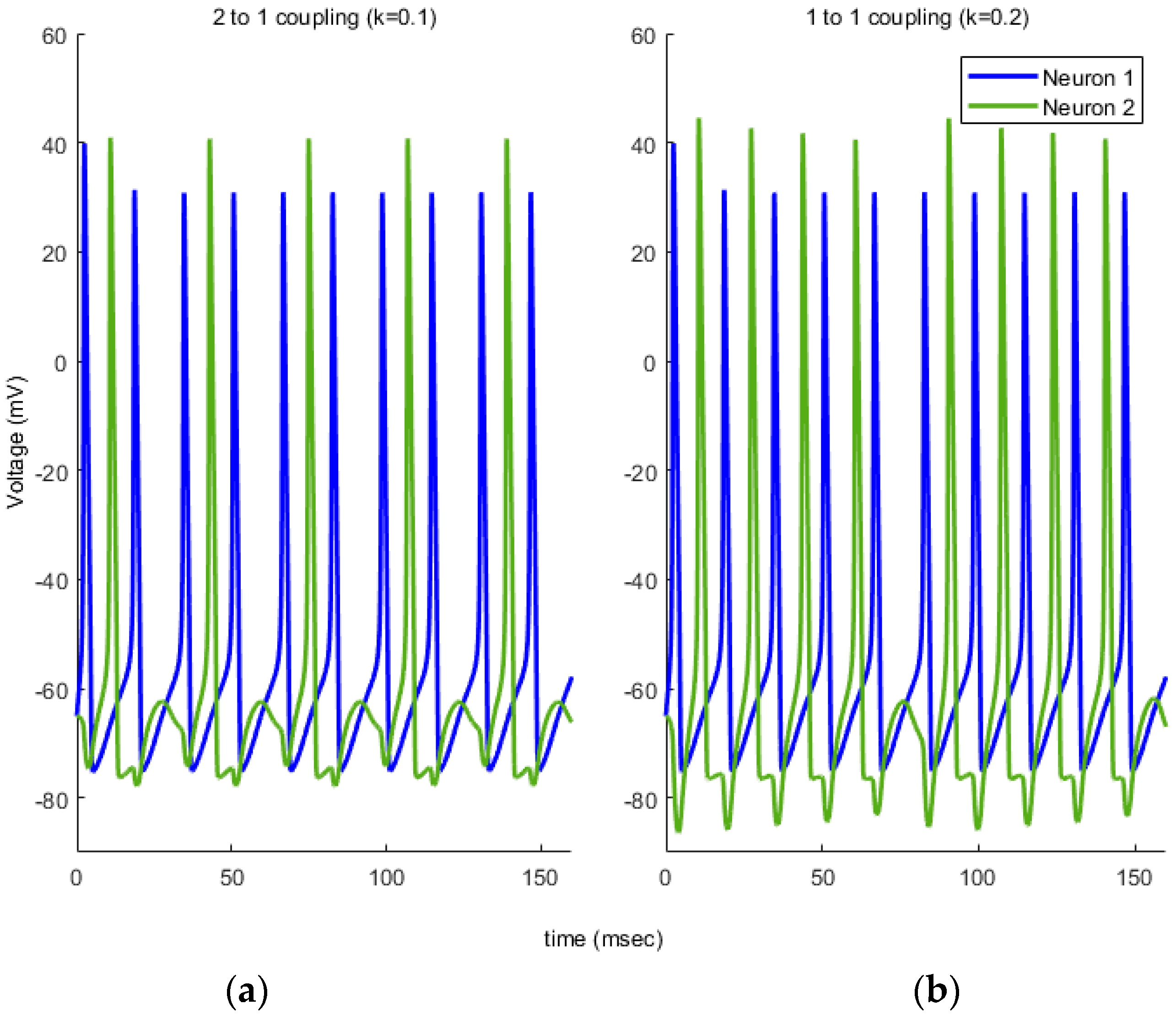
where $V_1$ is the membrane voltage for the 1st neuron and $V_2$ is the membrane voltage for the 2nd neuron. Here, $N(0,\sigma )$ shows the noise distribution defined by normal distribution with 0 mean and $\sigma$ standart deviation. Synapting coupling is defined simply $I_{syn}=k(V_2-V_1)$ with voltage difference and synaptic coupling strength is $k$. When k is between 0 and 0.25, spiking activity occurs with unique stable limit cycle solution. After k = 0.25 system turns back to stable steady state and spiking activity disappears. All other dynamics are same as described in Section 2.1.

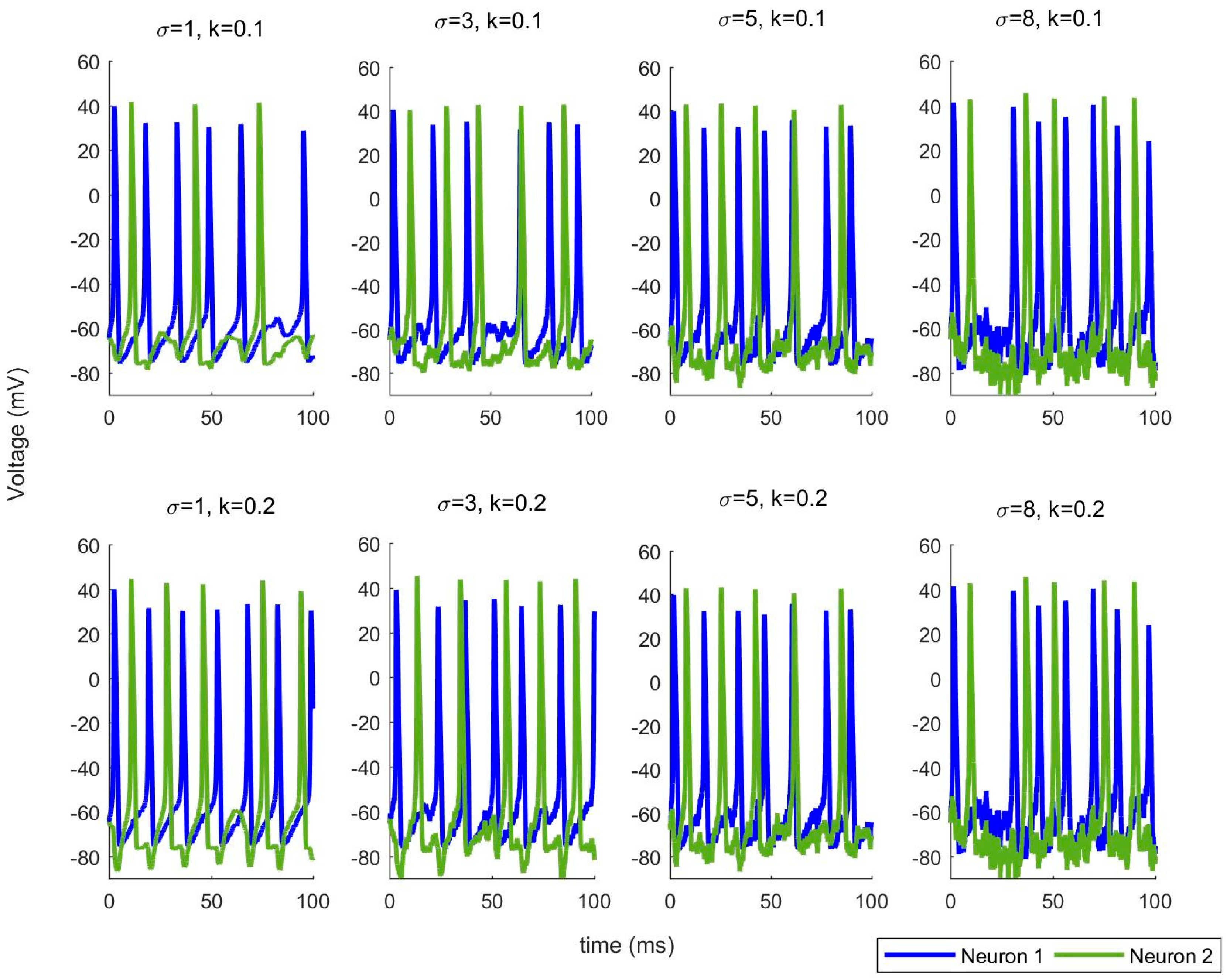
First, we propose using TE between $V_2 \mathrm{a}\mathrm{n}\mathrm{d} V_1$, in the case of no noise in (16) and (17). Secondly, we include the noise components in (16) and (17) and utilize TE between $V_2\mathrm{a}\mathrm{n}\mathrm{d}{V}_1$, again. This comparison demonstrates the effects of noise on the information flow between the neurons. At a first glance on equations (16) and (17), we can conclude that the direction of the information flow under noiseless case must be from $V_1\mathrm{t}\mathrm{o}{V}_2$. However, when the noise is added, it is tedius to reach the same conclusion, as the added noise is capable of adding additional spikes and destroying the available ones. The simulation results in the next section demonsrate these findings and provides promising results to generalize our model to more complex neuronal interactions under noise.

The model is implemented in the XPPAUT software [15] using the Euler method (dt = 0.1 ms).

3. Results

Information Flow Changes with Coupling Strength and Noise Level

Here, we first studied a system of two globally coupled HH model through a synapse by varying the coupling strength k, without noise effect. Phase dynamics for our system for two different k coupling strengths are plotted in Figure 1. Here we define two different coupling patterns as shown below. In Figure 1a, neuron 2 fires once after neuron 1 fires twice which we call 2-to-1 coupling with k = 0.1. For a larger coupling coefficient (k = 0.2) neurons shows different synchronous firing pattern as in Figure 1b. This time, each firing of neuron 2 follows that of neuron 1 which we call 1-to-1 coupling.

Here, we first studied a system of two globally coupled HH model through a synapse by varying the coupling strength k, without noise effect. Phase dynamics for our system for two different k coupling strengths are plotted in Figure 1. Here we define two different coupling patterns as shown below. In Figure 1a, neuron 2 fires once after neuron 1 fires twice which we call 2-to-1 coupling with k = 0.1. For a larger coupling coefficient (k = 0.2) neurons shows different synchronous firing pattern as in Figure 1b. This time, each firing of neuron 2 follows that of neuron 1 which we call 1-to-1 coupling.

To better understand the effects of noise on our network, we use zero mean Gaussian distributed random variables with standard deviation of $\sigma$. When we incorporate this noise with different variances into our model as illustrated in (16) and (17), we observe a change in the synchronisation of the neurons. Additionally, the obvious patterns disappear totally for larger noise amounts as shown in Figure 2 for each coupled network. Noise can change the synchronization of neurons by inducing or deleting spikes in network. Since the noise plays an important role in changing the dynamics of the network, we need a mechanism to figure out this newly changed patterns under noise effect to explain the behavior of the neuronal network. Therefore, we utilize TE to extract this pattern using the observed voltage data.

To better understand the information flow between the neurons, we estimate TE between the action potentials of two neurons, as described in Section 2.2, using (16) and (17), with an increasing noise intensity. The results are plotted in Figure 3 for both 2-to-1 coupled system and 1-to-1 coupled system. As expected for the network without noise ($\sigma$ = 0), transfer entropy value is the highest for both systems. This verifies the changes caused in Neuron 2 by Neuron 1.

To see the effects of noise, we explore the TE between the neurons with increasing $\sigma$ parameter. From Figure 3, we note that with the increasing noise intensity, the values of TE decrease. Although this can be expected, it is of utmost importance to emphasize the case when we do not have any noise. If we do not have noise component in the model, according to Figure 3 and

Table 2. Transfer entropy values with different noise intensity as $\sigma$.

$$\mathit{\sigma }$$	$$0$$	$$0.5$$	$$1$$	$$2$$	$$3$$	$$5$$	$$6$$	$$7$$	$$8$$	$$9$$	$$10$$
K = 0.1	0.0665	0.017	0.0168	0.0169	0.0129	0.0059	0.0039	0.0014	0.0013	0.000806	0.000512
K = 0.2	0.0557	0.0264	0.0206	0.0261	0.0242	0.0165	0.0148	0.0095	0.0064	0.0054	0.0033

, we notice that TE value is behaving in opposite way, i.e., the smaller TE, the higher coupling. Another interesting finding is the varying pattern in TE around low $\sigma$ values: The TE increases first and keeps decreasing later. This unexpected result shows that we cannot easily predict the direction of coupling without TE analysis, as the synaptic couplings are nonlinear in nature.

4. Discussion and Conclusions

We study information flow for the coupled network of two neurons under two different coupling states and increasing noise levels, where the neuron models and the synaptic interactions are derived from Hodgkin-Huxley model. Here we propose our model in such a way that we can generate 2-to-1 coupling and 1-to-1 coupling between the neurons. In order to find these relationships from data we propose a TE based approach and analyze the effects of couplings under various noise intensities, successfully. These results help us better understand the interaction between the neurons in real biological systems. This work is of particular importance to explore larger networks with more complex noisy interactions.