Haphazard Intentional Sampling Techniques in Network Design of Monitoring Stations ^†

Abstract

In empirical science, random sampling is the golden standard to ensure unbiased, impartial, or fair results, as it works as a technological barrier designed to prevent spurious communication or illegitimate interference between parties in the application of interest. However, the chance of at least one covariate showing a “significant difference” between two treatment groups increases exponentially with the number of covariates. In 2012, Morgan and Rubin proposed a coherent approach to solve this problem based on rerandomization in order to ensure that the final allocation obtained is balanced, but with an exponential computation cost in the number of covariates. Haphazard Intentional Sampling is a statistical technique that combines intentional sampling using goal optimization techniques with random perturbations. On one hand, it has all the benefits of standard randomization and, on the other hand, avoid exponentially large (and costly) sample sizes. In this work, we compare the haphazard and rerandomization methods in a case study regarding the re-engineering of the network of measurement stations for atmospheric pollutants. In comparison with rerandomization, the haphazard method provided groups with a better balance and permutation tests consistently more powerful.

1. Introduction

This paper addresses two related problems in the design of experiments: allocation and sampling.

The allocation problem can be illustrated with the classical example on clinical trials, see Fossaluza et al. [1]: Consider a research laboratory which wants to assess the effectiveness of a new drug for a particular disease. For this purpose, the laboratory may treat some patients with the new drug and others with a placebo. The problem of allocation consists of determining, for each patient in the trial, whether he/she will be treated with the new drug or the placebo. In order to obtain meaningful conclusions, researchers often wish the allocation to be balanced, in the sense that the distribution of some covariates (e.g., disease severity, gender, age, etc.) be the same among both treatment groups. This requirement is specially important to avoid spurious outcomes, such as different recovery rates due not to the effectiveness of each treatment, but to the imbalance in some of the covariates; for example, groups with a high proportion of patients with a mild form of the disease tend to have higher recovery rates than groups with a high proportion of patients with a severe form, even in the absence of treatment effect.

The sampling problem consists of drawing, from a (possibly large) set of sampling units or from a population, a subset for which some outcome variables shall be monitored. It is expected that the sample be a good representative of the whole original set, so that observations of outcomes in the sample can be used to make inferences about the whole set. As outcome variables may be influenced by some known covariates, a proxy to obtain such representative sampling is requiring that the distribution of these covariates be the same in the sample and in the remaining of complete set. In many practical applications, this problem may be considered analogous to the allocation problem, as it consists of partitioning the complete set of units into two groups—one composed by the sample and other the remaining (non monitored) units.

In both problems above, besides the requirement of obtaining well balanced groups, another fundamental requirement is that the allocation procedure be free of human ad-hoc interferences.

The standard solution for both problems is randomization, the golden standard to ensure unbiased, impartial, or fair results, see Pearl [2] and Stern [3]. Randomization works as a firewall, a technological barrier designed to prevent spurious communication of vested interests or illegitimate interference between parties in the application of interest, which may be a scientific experiment, a clinical trial, a legal case, an auditing process, or many other practical applications.

However, a common issue in randomized experiments is avoiding random allocations yielding groups that differ meaningfully with respect to relevant covariates. This is a critical issue, as the chance of at least one covariate showing a “significant difference” between two or more treatment groups increases exponentially with the number of covariates.

To overcome this issue, several authors suggest to repeat the randomization (i.e., to rerandomize) when it creates groups that are notably unbalanced on important covariates, see Sprott and Farewell [4], Rubin [5], Bruhn and McKenzie [6]. However, in the worst scenario, “ad hoc” rerandomization can be used to completely circumvent the haphazard, unpredictable or aimless nature of randomization, allowing a premeditated selection of a final outcome of choice, see Saa and Stern [7]. Another critique about rerandomization is that forms of analysis utilizing Gaussian distribution theory are no longer valid, as rerandomization changes the distribution of the test statistics, see Morgan and Rubin [8] and references therein.

As a response to these problems, Morgan and Rubin [8,9] proposed a coherent rerandomization approach in which the decision to rerandomize or not is based on a pre-specified criterion, e.g., a balance threshold. The inferential analysis of experimental data is based on a randomization test. The rerandomization procedure consists of the following steps:

1.

Select units for the comparison of treatments, and collect covariate data on all units.

2.

Define an explicit criterion for covariate balance.

3.

Randomize the units to treatment groups.

4.

Check covariate balance and return to Step 3 if the allocation is unacceptable according to the criterion specified in Step 2; continue until the balance is acceptable.

5.

Conduct the experiment using the final randomization obtained in Step 4.

6.

Perform inference (using a randomization test that follows exactly Steps 2–4).

Such approach aims to ensure balanced allocations, avoid subjective rejection criteria and provide sound inference procedures.

Despite the benefits of the above approach, it can be hard to use it in a way that yields a highly balanced allocation at a low computational cost. For example, in a problem of allocation into two groups, the probability that a simple random sampling generates an allocation that is significantly unbalanced (at level $\alpha$) for at least one out of d covariates is proportinal to $1-{(1-\alpha )}^d$. As a result, the expected number of rerandomizations that are required in order for the sample to be balanced in every covariate grows exponentially with the number of covariates.

The Haphazard Intentional Sampling is a statistical technique developed with the specific purpose of yielding sampling techniques that, on one hand, have all the benefits of standard randomization and, on the other hand, avoid exponentially large (and costly) sample sizes. This approach, proposed by Lauretto et al. [10,11] and Fossaluza et al. [1], can be divided into a randomization and an optimization step. The randomization step consists of creating new artificial covariates that are distributed according to a standard multivariate normal. The optimization step consists of finding the allocation that minimizes a linear combination of the imbalances in the original covariates and in the artificial covariates.

In this article, we apply the Haphazard Intentional Sampling techniques to study how to rationally re-engineer networks of measurement stations for atmospheric pollution and/or gas emissions. We show how such re-engineering or re-design can substantially decrease the operation cost of monitoring networks while providing, at the same time, support for arriving at conclusions or taking decisions with the same statistical power as in conventional setups.

2. Haphazard Intentional Sampling

In this section, we present the formulation of Haphazard Sampling originally presented at Lauretto et al. [11]. Let $\mathbf{X}$ denote the covariates of interest. $\mathbf{X}$ is a matrix in ${\mathbb{R}}^{n\times d}$, where n is the number of sampling units to be allocated and d is the number of covariates of interest.

An allocation consists of assigning to each unit a group chosen from a set of possible groups, $\mathcal{G}$. We denote an allocation, $\mathbf{w}$, by a $1\times n$ vector in ${\mathcal{G}}^n$.

For simplicity, we assume only two groups, that is, $\mathcal{G}=\{0,1\}$. We also assume that the number of units assigned to each group is previously defined. That is, there exist integers $n_1$ and $n_0$ such that $n_1+n_0=n$, $\mathbf{1}·{\mathbf{w}}^t=n_1$ and $\mathbf{1}·{(\mathbf{1}-\mathbf{w})}^t=n_0$.

The goal of the allocation problem is to generate an allocation that, with high probability, is close to the infimum of the imbalance between groups with respect to individual covariate values, measured by a loss function, $L(\mathbf{w},\mathbf{X})$.

An example of loss function is the Mahalanobis distance between the covariates of interest in each group [8], defined as follows. Let $\mathbf{A}$ be an arbitrary matrix in ${\mathbb{R}}^{n\times m}$. Furthermore, define ${\mathbf{A}}^{*}:=\mathbf{A}\mathbf{L}$, where $\mathbf{L}$ is the Cholesky decomposition [12] of the inverse of covariance matrix of $\mathbf{A}$; that is, $\mathrm{Cov}{\left(\mathbf{A}\right)}^{-1}={\mathbf{L}}^t\mathbf{L}$. For an allocation $\mathbf{w}$, let ${\overline{{\mathbf{A}}^{*}}}^1$ and ${\overline{{\mathbf{A}}^{*}}}^0$ denote the averages of each column of ${\mathbf{A}}^{*}$ over units allocated to, respectively, groups 1 and 0:

$${\overline{{\mathbf{A}}^{*}}}^1:=\frac{\mathbf{w}}{n_1}{\mathbf{A}}^{*}and{\overline{{\mathbf{A}}^{*}}}^0:=\frac{(\mathbf{1}-\mathbf{w})}{n_0}{\mathbf{A}}^{*}.$$

(1)

The Mahalanobis distance between the average of the column values of $\mathbf{A}$ in each group specified by $\mathbf{w}$ is defined as:

$$M(\mathbf{w},\mathbf{A}):=m^{-1}{\parallel {\overline{{\mathbf{A}}^{*}}}^1-{\overline{{\mathbf{A}}^{*}}}^0\parallel }_2.$$

(2)

In this work, the haphazard allocation consists of finding the minimum of a noisy version of the Mahalabonis loss function. Let $\mathbf{Z}$ be an artificially generated matrix in ${\mathbb{R}}^{n\times k}$, with elements that are independent and identically distributed according to the standard normal distribution. For a given tuning parameter, $\lambda \in [0,1]$, the haphazard allocation consists in solving the following optimization problem:

$$\begin{array}{cc}\mathrm{minimize}\hfill & {\displaystyle (1-\lambda )M(\mathbf{w},\mathbf{X})+\lambda M(\mathbf{w},\mathbf{Z})}\hfill \\ \text{subject to}\hfill & {\displaystyle \mathbf{1}·{\mathbf{w}}^t=n_1}\hfill \\ \hfill & {\displaystyle \mathbf{1}·{(\mathbf{1}-\mathbf{w})}^t=n_0}\hfill \\ \hfill & {\displaystyle \mathbf{w}\in {\{0,1\}}^n}\hfill \end{array}$$

(3)

The parameter $\lambda$ controls the amount of perturbation that is added to the original Mahalanobis loss function, $M(\mathbf{w},\mathbf{X})$. If $\lambda =0$, then $w^{*}$ is the deterministic minimizer of $M(\mathbf{w},\mathbf{X})$. If $\lambda =1$, then $w^{*}$ is the minimizer of the unrelated random loss, $M(\mathbf{w},\mathbf{Z})$. By choosing an intermediate value of $\lambda$ (as discussed in Section 4), one can obtain ${\mathbf{w}}^{*}$ to be a random allocation such that, with a high probability, $M({\mathbf{w}}^{*},\mathbf{X})$ is close to the infimum loss.

The formulation presented in Equation (3) is a Mixed-Integer Quadratic Programming Problem (MIQP) [13] and can be solved by the use of standard optimization software. As a MIQP may be computationally very expensive if n and d are large, a surrogate loss function that approximates $M(\mathbf{w},\mathbf{A})$ is a linear combination of the norms $l_1$ and $l_{\infty }$ as follows [14]:

$$H(\mathbf{w},\mathbf{A}):=m^{-1}\left(\parallel {\overline{{\mathbf{A}}^{*}}}^1-{\overline{{\mathbf{A}}^{*}}}^0{\parallel }_1+\sqrt{m}{\parallel {\overline{{\mathbf{A}}^{*}}}^1-{\overline{{\mathbf{A}}^{*}}}^0\parallel }_{\infty }\right)$$

(4)

The minimization of this hybrid norm yields a Mixed-Integer Linear Programming Problem (MILP), which is computationally much less expensive than a MIQP, see Murtagh [15], Wolsey and Nemhauser [13]:

$$\begin{array}{cc}\mathrm{minimize}\hfill & {\displaystyle (1-\lambda )H(\mathbf{w},\mathbf{X})+\lambda H(\mathbf{w},\mathbf{Z})}\hfill \\ \text{subject to}\hfill & {\displaystyle \mathbf{1}·{\mathbf{w}}^t=n_1}\hfill \\ \hfill & {\displaystyle \mathbf{1}·{(\mathbf{1}-\mathbf{w})}^t=n_0}\hfill \\ \hfill & {\displaystyle \mathbf{w}\in {\{0,1\}}^n}\hfill \end{array}$$

(5)

3. Case Study

CETESB—The Environmental Company of Sao Paulo State, maintains a network of atmospheric monitoring stations, which provide hourly records of pollutant indicators and atmospheric parameters (Raw data are freely available at http://qualar.cetesb.sp.gov.br/qualar/home.do). The problem here addressed is to select 25 of 54 candidate stations to install additional pollutant sensors which, due to their costs, could not be installed in all monitoring stations.

Eight parameters were considered to compute (and control) the Mahalanobis distance between groups: Particulate matter 10 micrometers (PM10), Nitrogen monoxide (NO), Nitrogen dioxide (NO2), Nitrogen oxides (NOx), Ozon (O3), Air temperature (Temp), Relative humidity (RH) and wind speed (WS). An R routine was adapted from Amorim [16] to collect data from CETESB web site and build a dataset with one-year observations (August 2017–July 2018). Data was summarized by taking the medians of observations separately for rainy (october–march) and dry (april–september) seasons. Station coordinates (latitude and longitude) were also considered, to induce a suitable geographic representativeness in the selected subsample. Thus, our matrix data $\mathbf{X}$ has a total of 18 covariates—8 atmospheric summaries for each rain/dry season plus station coordinates.

In our empirical study, we explore the trade-off between randomization and optimization by using well calibrated values for the parameter $\lambda$, as defined in the next equation. The transformation between parameters $\lambda$ and ${\lambda }^{*}$ is devised to equilibrate the weights given to the terms of Equations (3) and (5) corresponding to the covariates of interest and artificial, which have distinct dimensions, d and k.

$$\lambda ={\lambda }^{*}/\left[{\lambda }^{*}(1-k/d)+k/d\right],\mathrm{where}{\lambda }^{*}\in \{0.05,0.1,0.2,0.3,0.4\}.$$

(6)

For each value of ${\lambda }^{*}$, the haphazard allocation method was repeated 500 times (each time with a fresh random matrix of artificial covariates, $\mathbf{Z}$) with a fixed processing time $t=120$ s.

For comparison, we drew 500 allocations using the rerandomization method proposed by Morgan and Rubin [8], which in its original version consists of repeatedly drawing random allocations until $M(\mathbf{w},\mathbf{X})$ is below a given threshold a. Here we use a slightly modified fixed-time version of this method, that chooses the allocation which yields the lowest value for $M(\mathbf{w},\mathbf{X})$ with a given processing time budget $t=120$ s.

Finally, as a benchmark, we also drew 500 allocations using the standard (pure) randomization.

Computational tests were conducted on a desktop computer with a processor Intel I7-4930K (3.4 Ghz, 6 cores, 2 threads/core), Motherboard ASUS P9X79 LE, 24Gb RAM DDR3 and Linux Ubuntu Desktop v.18.04. The MILP problems were solved using Gurobi v.6.5.2 [17], a high performance solver that allows us to easily control all parameters of interest. Each allocation problem—among the batch of 500 allocations per allocation method, time budget and $\lambda$ value—was distributed to one of the 12 logical cores available. The computational routines were implemented in the R environment [18].

4. Results

4.1. Balance and Decoupling

Two performance criteria are analysed for each method:

• The balance criterion, measured by the Mahalanobis distance between the covariates of interest, $M({\mathbf{w}}^{*},\mathbf{X})$. We computed the median and 95th percentile of $M({\mathbf{w}}^{*},\mathbf{X})$ over the 500 allocations yielded by each method.
• The decoupling criterion, which concerns the absence of a systematic bias in allocating each pair of sampling units to the same group (positive association) or to different groups (negative association). For this purpose, we use the Yule’s coefficient of colligation [19]: for each pair of units $(i,j)\in {\{1,2,\dots ,n\}}^2,i<j$, and for each pair of groups $(r,s)\in {\{0,1\}}^2$, let $z_{rs}(i,j)$ denote the number of times among the 500 allocations such that the units i and j are assigned, respectively, to groups r and s. The Yule coefficient for the pair $(i,j)$ is computed as

  $$Y(i,j)=\frac{\sqrt{z_{00}(i,j)z_{11}(i,j)}-\sqrt{z_{01}(i,j)z_{10}(i,j)}}{\sqrt{z_{00}(i,j)z_{11}(i,j)}+\sqrt{z_{01}(i,j)z_{10}(i,j)}}.$$

  (7)
  This coefficient ranges in the interval $[-1,1]$ and measures how often the units $(i,j)$ are allocated to the same or to different groups. It equals zero when the numbers of agreements (allocations to the same group) and disagreements (allocations to different groups) are equal; and is maximum ($-1$ or $+1$) in the presence of total negative (complete disagreement) or positive (complete agreement) association.
  The closer the $Y(i,j)$ to $+1$ or $-1$, the lower the decoupling provided by the allocation method with respect to $(i,j)$. So, for comparison purposes, we computed, for each method, the median and 95th percentile of $\left|Y\right(i,j\left)\right|$ among all pairs $(i,j)$.

Table 1. Mahalobis distances and absolute Yule coefficients yielded by the haphazard allocation, rerandomization and pure randomization methods (500 allocations for each method).

Method	Mahalanobis Distance		Yule Coefficient (Absolute Value)
	Median	95th perc.	Median	95th perc.
Haphazard (${\lambda }^{*}=0.05$)	0.15	0.17	0.26	0.71
Haphazard (${\lambda }^{*}=0.10$)	0.16	0.18	0.16	0.51
Haphazard (${\lambda }^{*}=0.20$)	0.18	0.20	0.12	0.45
Haphazard (${\lambda }^{*}=0.30$)	0.18	0.21	0.12	0.44
Haphazard (${\lambda }^{*}=0.40$)	0.20	0.22	0.11	0.43
Rerandomization	0.44	0.48	0.07	0.26
Pure random	1.15	1.40	0.03	0.07

shows the median and 95th percentile for the Mahalanobis distances and absolute Yule coefficients for each method. As expected, the pure randomization method yields the highest Mahalanobis distances, as it does not take into account the balance between groups. For the haphazard method, the lower the ${\lambda }^{*}$ (and therefore, the lower the random component weight), the lower the Mahalanobis distance. It can be noticed that, for all values of ${\lambda }^{*}$ considered, the haphazard method yielded the lowest values for median and 95th percentile (outperforming the rerandomization method by a factor between 2 and 3). That means that the risk of getting a very bad allocation with the haphazard method is much smaller than using the rerandomization or pure randomization methods. Regarding the Yule coefficient, the pure randomization method is the benchmark for this parameter, as it naturally precludes any systematic association between individual allocations. For the haphazard allocation method, the Yule coefficient decreases as ${\lambda }^{*}$ increases.

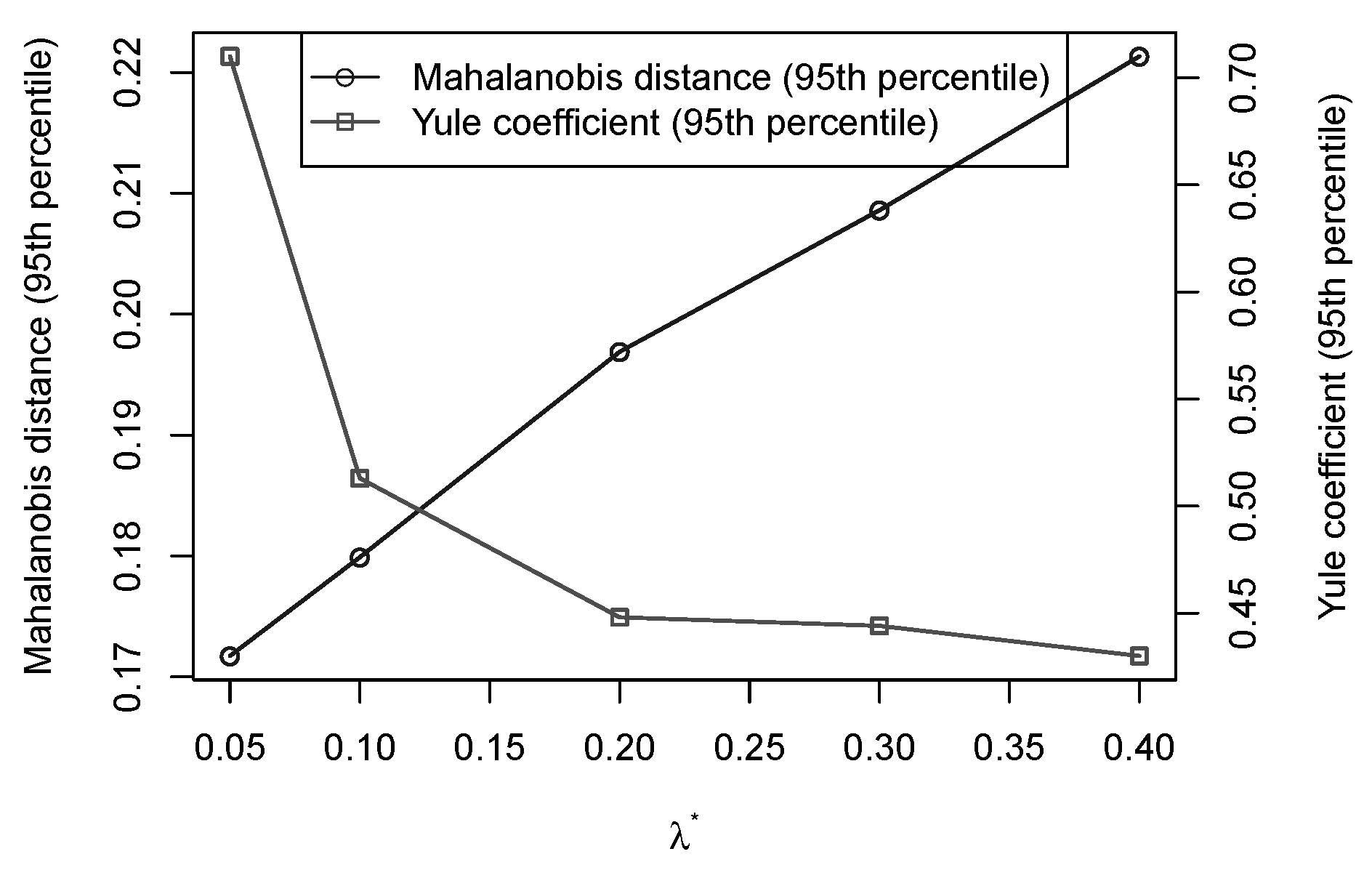
The choice of the most suitable value of ${\lambda }^{*}$ among the candidate values in Table 1 is based on a graphical analysis, shown in Figure 1, in which we compare the variation rates of Mahalanobis distances and Yule coefficients with respect to ${\lambda }^{*}$. It can be noticed that, whereas the Mahalanobis distance increases almost linearly with ${\lambda }^{*}\in \{0.05,0.1,0.2,0.3,0.4\}$, the Yule coefficient decreases initially very fast for ${\lambda }^{*}\le 0.2$ but afterward gets less sensitive with respect to ${\lambda }^{*}$. This suggests that, for our case study, ${\lambda }^{*}=0.2$ is the most suitable choice, as values downward this point yield slightly lower Mahalanobis distances, but much higher Yule coefficients; conversely, values upward this point yield only slightly lower Yule coefficients, but considerably higher Mahalanobis distances.

In comparison with rerandomization, haphazard method set with ${\lambda }^{*}=0.2$ yielded a 95th percentile for the Mahalanobis distances $140\%$ better (0.20 vs. 0.48), with a 95th percentile for the Yule coefficient which is $73\%$ higher (0.45 vs. 0.26).

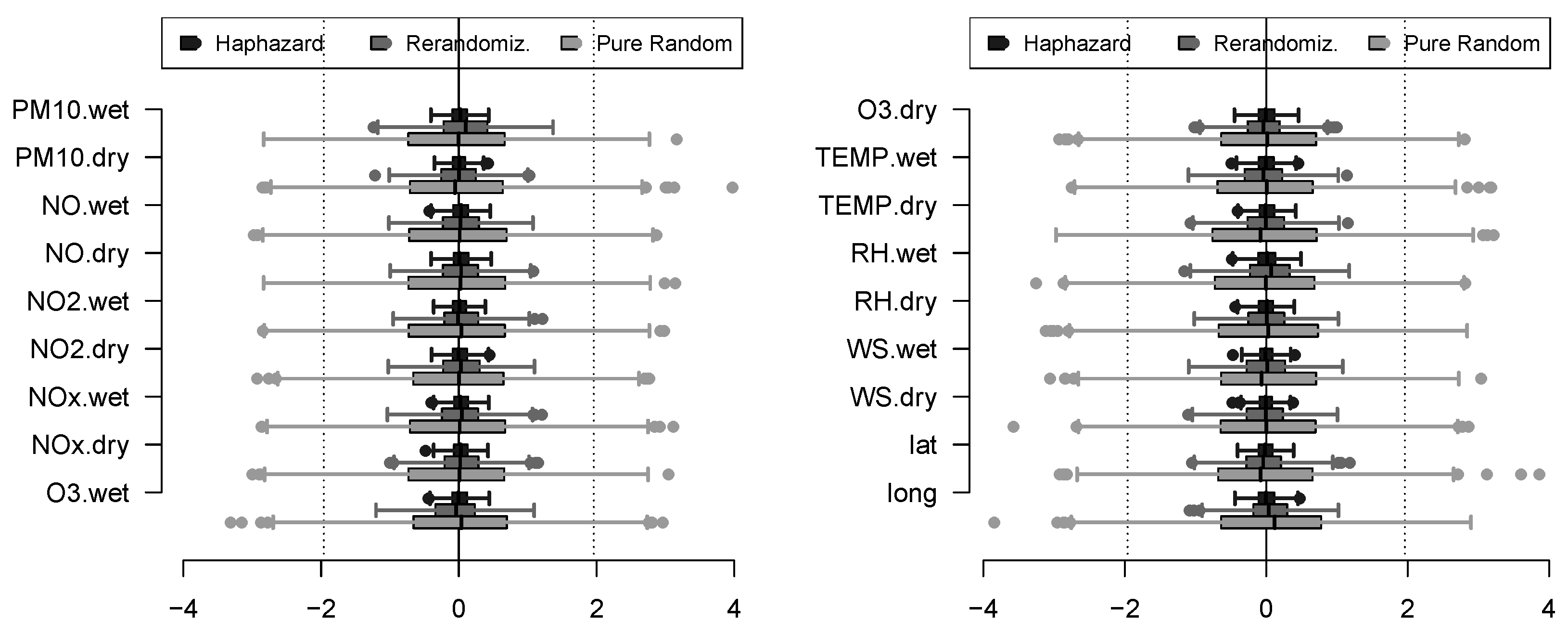
Figure 2 illustrates the empirical distributions for the standardized difference in means for each covariate, each based on 500 simulated allocations per method. Each horizontal box plot represents, for each method and each covariate j, the empirical distribution of the statistics $({\overline{\mathbf{X}}}_{,j}^1-{\overline{\mathbf{X}}}_{,j}^0)/s_j$, where ${\overline{\mathbf{X}}}_{,j}^1$ and ${\overline{\mathbf{X}}}_{,j}^0$ denote the averages of the j-th column of $\mathbf{X}$ over units allocated to, respectively, groups 1 and 0 (see Equation (1)); and $s_j$ is the reference scale given by the standard deviation of ${\overline{\mathbf{X}}}_{,j}^1-{\overline{\mathbf{X}}}_{,j}^0$ computed over 500 simple random allocations. It can be easily seen that differences are remarkably smaller in haphazard allocations than in rerandomization method that, in turn, are remarkably smaller than using pure randomization.

4.2. Inference Power

The above measures can also be seen as a proxy for optimizing other statistical properties. For instance, one might be interested in testing the existence of a causal effect of the group assignment on a given response variable Y.

Consider that, for each $r\in \{0,1\}$, define ${\mathit{\mu }}^r$ to be a $1\times n$ vector where ${\mu }_i^r$ is the expected outcome for unit i under treatment assign r, i.e., ${\mu }_i^r=E\left(Y_i\right|w_i=r)$. Define $\tau$ to be the true average treatment effect in the sample,

$$\tau =\frac{\mathbf{1}·{\left({\mathit{\mu }}^1\right)}^t}{n}-\frac{\mathbf{1}·{\left({\mathit{\mu }}^0\right)}^t}{n}.$$

(8)

Denoting by $\mathbf{w}$ the allocation and by $\mathbf{y}$ the vector of observations for Y after units have received the corresponding treatments, $\tau$ can be estimated by:

$${\widehat{\tau }}_{\mathbf{w},\mathbf{y}}=\frac{\mathbf{w}·{\mathbf{y}}^t}{n_1}-\frac{(1-\mathbf{w})·{\mathbf{y}}^t}{n_0}.$$

(9)

Suppose the problem of interest is testing the hypothesis that treatment effect is null, that is, $H_0:\tau =0$.

A randomization test consists in simulating a reference distribution for $\widehat{\tau }$ under the hypothesis $H_0$, and then estimating the probability of getting an estimate more extreme than the observed value of ${\widehat{\tau }}_{\mathbf{w},\mathbf{y}}$. Considering a two-tailed test, a significance level $\alpha$ and the allocation method $\mathcal{M}\left(\mathbf{X}\right)$ used to conduct the experiment, the randomization test follows the following steps:

1.

Generate B allocations ${\mathbf{w}}^{\left(1\right)},{\mathbf{w}}^{\left(2\right)},\dots ,{\mathbf{w}}^{\left(B\right)}$ using method $\mathcal{M}\left(\mathbf{X}\right)$, constrained to $\mathbf{1}·{\left({\mathbf{w}}^{\left(b\right)}\right)}^t=n_1$ and $\mathbf{1}·{(\mathbf{1}-{\mathbf{w}}^{\left(b\right)})}^t=n_0$.

2.

For each generated allocation ${\mathbf{w}}^{\left(b\right)}$, compute the corresponding ${\widehat{\tau }}_{{\mathbf{w}}^{\left(b\right)},\mathbf{y}}$ according to Equation (9).

3.

Estimate the p value by

$$p\cong \frac{{\sum }_{b=1}^{B}I\left(\right|{\widehat{\tau }}_{{\mathbf{w}}^{\left(b\right)},\mathbf{y}}|\ge |{\widehat{\tau }}_{\mathbf{w},\mathbf{y}}\left|\right)}{B},$$

(10)

where $I(·)$ is the indicator function.

4.

$H_0$ is rejected if $p\le \alpha$.

We performed a numerical experiment to assess the test power (i.e., the probability of rejecting $H_0$ when it is false) in the allocations obtained by each allocation method in this study. For this purpose, for each method $\mathcal{M}\left(\mathbf{X}\right)$ and for each $\tau \in \{0,0.1,0.2,\dots ,2\}$, we repeated 500 times the following procedure:

1.

Generate an allocation $\mathbf{w}$ using the method $\mathcal{M}\left(\mathbf{X}\right)$.

2.

Simulate a response vector $\mathbf{y}$ in the following way:

For $i\in \{1,\dots ,n\}$:

• Draw a random number ${\mu }_i^0\sim N(\theta ,1)$, where $\theta ={\sum }_j\left(X_{i,j}-{\overline{X}}_{,j}\right)/\mathrm{sd}\left(X_{,j}\right)$ and j indexes the columns of $\mathbf{X}$;
• If $w_i=0$, then set $y_i={\mu }_i^0$; otherwise, set $y_i={\mu }_i^0+\tau$.

3.

Apply the randomization test described above on $\mathbf{w},\mathbf{y}$ to test $H_0:\tau =0$, with a significance level $\alpha =0.05$ and $B=500$ allocations.

For each value of $\tau$, the test power is estimated by the proportion of times the hypothesis $H_0$ has been rejected over the 500 repetitions of the procedure above. It is expected that this probability equals to $\alpha$ for $\tau =0$, and approaches 1 as $\tau$ increases.

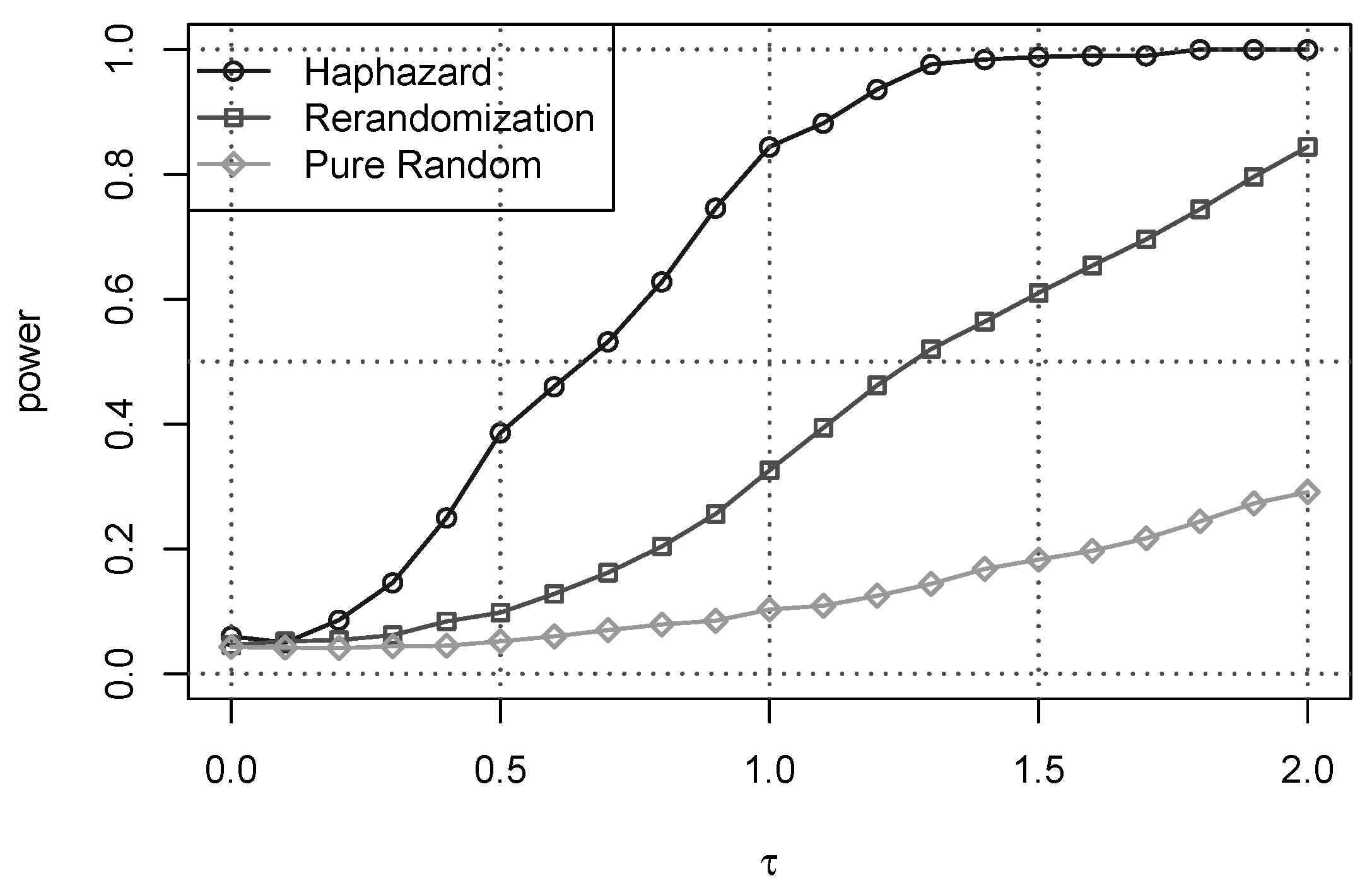
Figure 3 illustrates the difference of power in the allocations obtained by the haphazard (${\lambda }^{*}=0.2$), fixed-time rerandomization and pure randomization methods for the hypothesis $H_0:\tau =0$. The tests obtained using the haphazard allocations are consistently more powerful over $\tau$ than the ones obtained using the rerandomization allocations. Indeed, for $\tau \in [0.3,1.2]$, the power yielded by haphazard allocations is more than twice the power yielded by rerandomized allocations, with a maximum factor of $3.9$ for $\tau =0.5$.

5. Conclusions

Results presented in this paper indicate that the haphazard intentional allocation method is a promising tool for design of experiments. In the numerical experiment conducted, the haphazard allocation method outperformed the alternative fixed-time rerandomization method by a factor $2.4$ concerning the loss function of imbalance between the allocated groups. Besides, permutation tests using haphazard allocations are consistently more powerful than those obtained using the rerandomization allocations.

Future works shall explore the use of the Haphazard Intentional Allocation method and the Rerandomization method in applied problems in the fields of environmental monitoring, clinical trials, jurimetrics and audit procedures. We shall also explore the use of alternative surrogate Loss functions for balance performance, such as CVaR norms, Deltoidal norms and Block norms, see Pavlikov and Uryasev [20], Gotoh and Uryasev [21], Ward and Wendell [22].