Learning Model Discrepancy of an Electric Motor with Bayesian Inference †
Abstract
:1. Introduction
2. Electric Motor Model
3. Bayesian Inference Solution Process
3.1. Bayesian Model 1 (BM1): Measurement Noise
3.2. Bayesian Model 2 (BM2): Measurement Noise and Model Discrepancy
4. Numerical Results
4.1. Results Bayesian Model 1
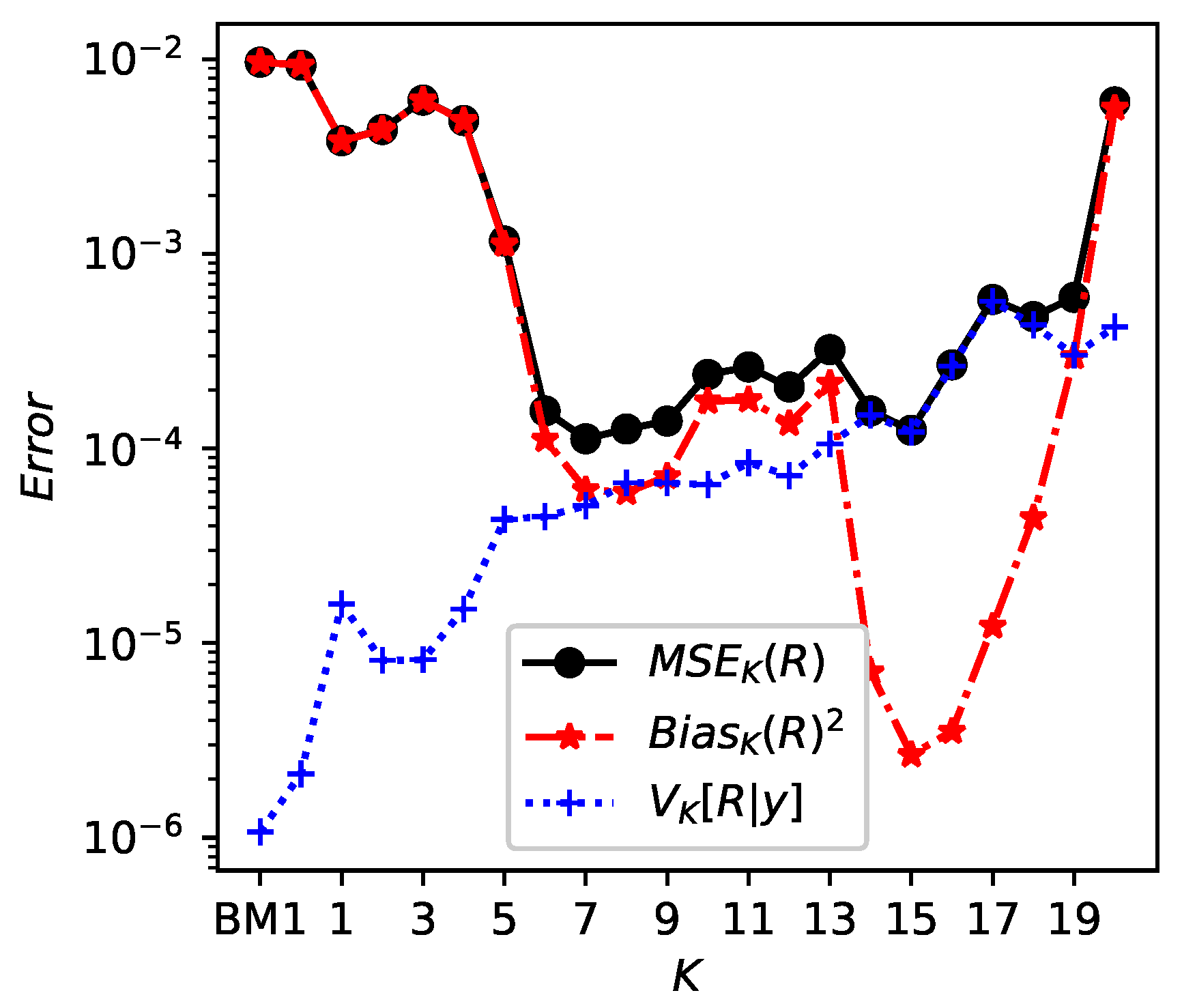
4.2. Results Bayesian Model 2
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Kaipio, J.; Somersalo, E. Statistical and Computational Inverse Problems; Applied Mathematical Sciences; Springer Science+Business Media, Inc.: New York, NY, USA, 2005. [Google Scholar]
- Stuart, A.M. Inverse problems: A Bayesian perspective. Acta Numer. 2010, 19, 451–559. [Google Scholar] [CrossRef]
- Dashti, M.; Stuart, A.M. The Bayesian Approach to Inverse Problems. In Handbook of Uncertainty Quantification; Ghanem, R., Higdon, D., Owhadi, H., Eds.; Springer: Cham, Switzerland, 2017; pp. 311–428. [Google Scholar]
- Gelman, A.; Carlin, J.B.; Stern, H.S.; Dunson, D.B.; Vehtari, A.; Rubin, D.B.; Stern, H.S. Bayesian Data Analysis, 3rd ed.; Texts in Statistical Science Series; CHAPMAN & HALL/CRC and CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Sullivan, T.J. Introduction to Uncertainty Quantification; Texts in Applied Mathematics 0939-2475; Springer: Berlin, Germany, 2015; Volume 63. [Google Scholar]
- Hastings, W.K. Monte Carlo Sampling Methods Using Markov Chains and Their Applications. Biometrika 1970, 57, 97. [Google Scholar] [CrossRef]
- Salvatier, J.; Wiecki, T.V.; Fonnesbeck, C. Probabilistic programming in Python using PyMC3. PeerJ Comput. Sci. 2016, 2, e55. [Google Scholar] [CrossRef]
- Schillings, C.; Schwab, C. Scaling limits in computational Bayesian inversion. ESAIM Math. Model. Numer. Anal. 2016, 50, 1825–1856. [Google Scholar] [CrossRef]
- Sprungk, B. Numerical Methods for Bayesian Inference in Hilbert Spaces, 1st ed.; Universitätsverlag der TU Chemnitz: Chemnitz, Germany, 2018. [Google Scholar]
- Hoffman, M.D.; Gelman, A. The No-U-turn sampler: adaptively setting path lengths in Hamiltonian Monte Carlo. J. Mach. Learn. Res. 2014, 15, 1593–1623. [Google Scholar]
- Xiu, D.; Karniadakis, G.E. The Wiener-Askey polynomial chaos for stochastic differential equations. SIAM J. Sci. Comput. 2002, 24, 619–644. [Google Scholar] [CrossRef]
- Glaser, P.; Schick, M.; Petridis, K.; Heuveline, V. Comparison between a Polynomial Chaos surrogate model and Markov Chain Monte Carlo for inverse Uncertainty Quantification based on an electric drive test bench. In Proceedings of the ECCOMAS Congress 2016, Crete Island, Greece, 5–10 June 2016. [Google Scholar]
- Kennedy, M.C.; O’Hagan, A. Bayesian calibration of computer models. J. R. Stat. Soc. Ser. B Stat. Methodol. 2001, 63, 425–464. [Google Scholar] [CrossRef]
- Rasmussen, C.E.; Williams, C.K. Gaussian Process for Machine Learning; MIT Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Arendt, P.D.; Apley, D.W.; Chen, W. Quantification of Model Uncertainty: Calibration, Model Discrepancy, and Identifiability. J. Mech. Des. 2012, 134, 100908. [Google Scholar] [CrossRef]
- Arendt, P.D.; Apley, D.W.; Chen, W.; Lamb, D.; Gorsich, D. Improving Identifiability in Model Calibration Using Multiple Responses. J. Mech. Des. 2012, 134, 100909. [Google Scholar] [CrossRef]
- Paulo, R.; García-Donato, G.; Palomo, J. Calibration of computer models with multivariate output. Comput. Stat. Data Anal. 2012, 56, 3959–3974. [Google Scholar] [CrossRef]
- Brynjarsdóttir, J.; O’Hagan, A. Learning about physical parameters: The importance of model discrepancy. Inverse Probl. 2014, 30, 114007. [Google Scholar] [CrossRef]
- Tuo, R.; Wu, C.F.J. Efficient calibration for imperfect computer models. Ann. Stat. 2015, 43, 2331–2352. [Google Scholar] [CrossRef]
- Tuo, R.; Jeff Wu, C.F. A Theoretical Framework for Calibration in Computer Models: Parametrization, Estimation and Convergence Properties. SIAM/ASA J. Uncertain. Quantif. 2016, 4, 767–795. [Google Scholar] [CrossRef]
- Plumlee, M. Bayesian Calibration of Inexact Computer Models. J. Am. Stat. Assoc. 2016, 112, 1274–1285. [Google Scholar] [CrossRef]
- Nagel, J.B.; Rieckermann, J.; Sudret, B. Uncertainty Quantification in Urban Drainage Simulation: Fast Surrogates for Sensitivity Analysis and Model Calibration. 2017. Available online: http://arxiv.org/abs/1709.03283 (accessed on 23 March 2018).
- Toliyat, H.A. (Ed.) Handbook of Electric Motors, 2nd ed.; Electrical and Computer Engineering; Dekker: New York, NY, USA; Basel, Switzerland, 2004; Volume 120. [Google Scholar]
- Wanner, G.; Hairer, E. Solving Ordinary Differential Equations I; Springer: Berlin, Germany, 1991; Volume 1. [Google Scholar]
- Kotz, S.; Kozubowski, T.; Podgorski, K. The Laplace Distribution and Generalizations: A Revisit with Applications to Communications, Economics, Engineering, and Finance; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J.H. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Springer Series in Statistics; Springer: New York, NY, USA, 2009. [Google Scholar]
- John, D.; Schick, M.; Heuveline, V. Learning model discrepancy of an electric motor with Bayesian inference. Eng. Math. Comput. Lab 2018. [Google Scholar] [CrossRef]
| Marginal Posterior Mean | Relative Error | |||||
|---|---|---|---|---|---|---|
| BM1 | 9.03 × | 6.29 × | 1.03 × | 9.66 × | 2.14 × | 2.79 × |
| BM2 () | 9.92 × | 2.02 × | 9.95 × | 8.48 × | 1.03 × | 4.89 × |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
John, D.N.; Schick, M.; Heuveline, V. Learning Model Discrepancy of an Electric Motor with Bayesian Inference. Proceedings 2019, 33, 11. https://doi.org/10.3390/proceedings2019033011
John DN, Schick M, Heuveline V. Learning Model Discrepancy of an Electric Motor with Bayesian Inference. Proceedings. 2019; 33(1):11. https://doi.org/10.3390/proceedings2019033011
Chicago/Turabian StyleJohn, David N., Michael Schick, and Vincent Heuveline. 2019. "Learning Model Discrepancy of an Electric Motor with Bayesian Inference" Proceedings 33, no. 1: 11. https://doi.org/10.3390/proceedings2019033011
APA StyleJohn, D. N., Schick, M., & Heuveline, V. (2019). Learning Model Discrepancy of an Electric Motor with Bayesian Inference. Proceedings, 33(1), 11. https://doi.org/10.3390/proceedings2019033011




