A Novel Method for LWIR Hyperspectral Target Detection by Means of a Subspace-Based Approach ^†

Abstract

In this work, we present a new approach to detect materials with known spectral emissivity, in data acquired by thermal infrared hyperspectral systems. The method takes into account the spectral variability of the downwelling radiance, commonly neglected in most target detection techniques. We address such variability supposing that the downwelling radiance spans a low-rank subspace, whose basis matrix is learned off-line by means of MODTRAN. We evaluate the performance of the method with simulated data, and present results that show the effectiveness of the proposed algorithm.

1. Introduction

In LWIR hyperspectral systems, target detection is accomplished exploiting the spectral emissivity of the target-of-interest (TOI) [1]. The signal processing chain that leads to detect the TOI within the monitored scene may be split in three steps: atmospheric correction, downwelling spectral radiance estimation, and target detection. Atmospheric correction consists in estimating the ground leaving radiance by removing the contributions due to the spectral transmittance and upward radiance [2]. The task of estimating the downwelling radiance is often difficult, because a down-looking sensor cannot acquire knowledge of the atmosphere above the platform, this is especially true for airborne sensors [3]. A valuable solution was proposed in [4]. The third step is the application of a target detection technique, which can be applied in the spectral emissivity domain [1], or in the spectral radiance domain [5]. Generally, the papers published in this field commonly exploit the hypothesis that the atmosphere is known [6,7,8,9]. In this work, we present a new target detection algorithm that accounts for the spectral variability of the downwelling radiance by means of a subspace-based model (we suppose that the atmospheric correction has been already accomplished). The method performs the task in the radiance domain, i.e. the TOI spectral emissivity is transformed in TOI spectral radiance accounting for the downwelling radiance estimate. The proposed approach does not require the accurate knowledge of the downwelling radiance vector, and assumes that such vector belongs to a subspace having rank lower than the number of spectral channels.

2. Materials and Method

2.1. Algorithm Description

We denote as ${\mathbf{L}}_{\mathbf{gl}}$ the $N_c\times 1$ vector whose components are the spectral samples of the ground-leaving radiance taken at the central wavelengths ${\lambda }_1,...,{\lambda }_{N_c}$ of the adopted hyperspectral sensor. In the LWIR, the at-sensor radiance vector ${\mathbf{L}}_{\mathbf{gl}}$ can be expressed by the following Radiative Transfer Model (RTM) [3]

$${\mathbf{L}}_{\mathbf{gl}}={\mathbf{D}}_{\mathit{ϵ}}{\mathbf{L}}_{\mathbf{BB}}\left(T\right)+\left[\mathbf{I}-{\mathbf{D}}_{\mathit{ϵ}}\right]{\mathbf{L}}_{\downarrow }+\mathbf{N}$$

(1)

where ${\mathbf{D}}_{\mathit{ϵ}}$ represents the $N_c\times N_c$ diagonal matrix whose diagonal entries are the samples of the material spectral emissivity $\mathit{ϵ}$, ${\mathbf{L}}_{\mathbf{BB}}\left(T\right)$ and ${\mathbf{L}}_{\downarrow }$ are the $N_c\times 1$ vectors of the spectral radiance of a blackbody at temperature T (Planck’s law), and the spectral downwelling radiance, respectively; $\mathbf{I}$ is the $N_c\times N_c$ identity matrix. $\mathbf{N}$ is the $N_c\times 1$ noise vector after atmospheric correction. The latter can be modeled as described in [2].

We exploit the signal model to formulate the detection task as a one-class classification problem. Specifically, we decide the presence of the TOI comparing the observed ground-leaving radiance with its model reconstruction obtained according to Equation (1), exploiting the emissivity spectrum we want to detect. To accomplish the task, we use the Relative Error (RE) defined as:

$$\mathrm{RE}\left[\overline{\mathit{ϵ}},T,{\mathbf{L}}_{\downarrow }\right]=\parallel {\mathbf{L}}_{\mathbf{gl}}-{\widehat{\mathbf{L}}}_{\mathbf{gl}}\left(\overline{\mathit{ϵ}},T,{\mathbf{L}}_{\downarrow }\right){\parallel }_2/{\parallel {\mathbf{L}}_{\mathbf{gl}}\parallel }_2$$

(2)

where ${\parallel ·\parallel }_{{}_2}$ denotes the $l_{{}_2}$-norm and ${\widehat{\mathbf{L}}}_{\mathbf{gl}}\left(\overline{\mathit{ϵ}},T,{\mathbf{L}}_{\downarrow }\right)$ is the reconstruction of ${\mathbf{L}}_{\mathbf{gl}}$, obtained exploiting the model in Equation (1) by setting $\mathit{ϵ}=\overline{\mathit{ϵ}}$, with $\overline{\mathit{ϵ}}$ the emissivity spectrum of the TOI. We claim the presence of the TOI if RE is lower than a given threshold. Unfortunately, T and ${\mathbf{L}}_{\downarrow }$ in Equation (2) are uknown, and must be replaced with their estimates obtained by the observed ${\mathbf{L}}_{\mathbf{gl}}$. Supposing $\mathit{ϵ}$ known, the estimate represents an ill-posed problem, because the number of unknowns ($N_c+1$) is higher than the number of observations ($N_c$). To solve the indeterminateness, we suppose that the vectors ${\mathbf{L}}_{\downarrow }$ span a linear subspace featuring a rank $K<N_c$, i.e. ${\mathbf{L}}_{\downarrow }=\mathbf{A}\mathbf{b}$, where $\mathbf{A}\in {\mathrm{I}\mathrm{R}}^{N_c\times K}$ is the basis matrix of such a subspace, and $\mathbf{b}\in {\mathrm{I}\mathrm{R}}^{K\times 1}$ is the vector of the coefficients of ${\mathbf{L}}_{\downarrow }$ with respect to $\mathbf{A}$. The latter subspace model (assumed as known) allows us to reformulate the unknown problem so as to have T and $\mathbf{b}$ as unknowns, given $N_c>K+1$ observations:

$$\mathrm{RE}\left[\overline{\mathit{ϵ}},T,\mathbf{b}\right]=\parallel {\mathbf{L}}_{\mathbf{gl}}-{\widehat{\mathbf{L}}}_{\mathbf{gl}}\left(\overline{\mathit{ϵ}},T,\mathbf{b}\right){\parallel }_2/{\parallel {\mathbf{L}}_{\mathbf{gl}}\parallel }_2$$

(3)

We obtain T and $\mathbf{b}$ solving the following minimization problem:

$$\left[\begin{array}{c}\widehat{T}\\ \widehat{\mathbf{b}}\end{array}\right]=arg\underset{\eta \in \left[T_L,T_H\right]}{min}\left[\underset{\beta }{min}\mathrm{RE}\left[\overline{\mathit{ϵ}},\eta ,\beta \right]\right]$$

(4)

where $\beta$ is chosen within ${\mathrm{I}\mathrm{R}}^{K\times 1}$, and $\eta$ selected within a given temperature interval $\left[T_L,T_H\right]$. Equation (4) can be simplified observing that given a guess of the target temperature $\overline{\eta }$, the optimum estimate of $\mathbf{b}$ is obtained from the observed radiance as least square solution as follows:

$$\widehat{\mathbf{b}}\left(\overline{\eta }\right)={\mathbf{A}}^{+}{\mathbf{L}}_{\downarrow }^{\mathbf{inv}}\left(\overline{\eta }\right)$$

(5)

where ${\mathbf{A}}^{+}$ is the pseudo-inverse matrix of $\mathbf{A}$, and ${\mathbf{L}}_{\downarrow }^{\mathbf{inv}}\left(\overline{\eta }\right)$ is

$${\mathbf{L}}_{\downarrow }^{\mathbf{inv}}\left(\overline{\eta }\right)={\left[\mathbf{I}-{\mathbf{D}}_{\overline{\mathit{ϵ}}}\right]}^{-1}\left[{\mathbf{L}}_{\mathbf{gl}}-{\mathbf{D}}_{\overline{\mathit{ϵ}}}{\mathbf{L}}_{\mathbf{BB}}\left(\overline{\eta }\right)\right]$$

(6)

Substituting Equation (5) inside Equation (4), the problem is rewritten with T as the only unknown parameter:

$$\widehat{T}=arg\underset{\eta \in \left[T_L,T_H\right]}{min}\mathrm{RE}\left[\overline{\mathit{ϵ}},\eta ,\widehat{\mathbf{b}}\left(\eta \right)\right]$$

(7)

Equation (7) can be solved by resorting to a greedy algorithm. $\mathrm{RE}\left[\overline{\mathit{ϵ}},\widehat{T},\widehat{\mathbf{b}}\left(\widehat{T}\right)\right]$ is the statistic for the detection task.

2.2. Determination of the Basis Matrix $\mathbf{A}$

A possible approach to estimate the basis matrix $\mathbf{A}$ is the one adopted in [2]. We suppose that in the portion of the LWIR spectral range, the variability of ${\mathbf{L}}_{\downarrow }$, due to the atmospheric parameters such as the integrated water vapor, atmospheric pressure and temperature, can be well represented on a subspace having a rank $K<N_c$. Thus, we exploit MODTRAN to construct a dictionary of spectral downwelling radiances, parameterized with respect to the variation of those parameters, and extract the low-rank basis matrix $\mathbf{A}$ from such a dictionary by means of the Singular Value Decomposition (SVD) algorithm.

2.3. Simulation Strategy

To prove the effectiveness of the detection technique, we derived ground-leaving radiance data starting from two available online spectral emissivity databases [10,11], for a total amount of 216 emissivity spectra. We selected 4 materials (Figure 1a), as TOIs to be searched within the "background", represented by the remaining 212 spectra. We generated ${\mathbf{L}}_{\downarrow }$ vectors by means of MODTRAN, considering the standard mid-latitude summer atmospheric model, and by assuming a nadir-view from an airborne with a flight altitude of 1Km. The downwelling radiance vectors, the surface temperatures, and the emissivity spectra are combined according to Equation (1) to obtain the ground-leaving radiances of both the TOI, and of the “background”. The temperatures are drawn from an uniform distribution in the interval $\left[{20}^{\circ }-{50}^{\circ }\right]$C. The ${\mathbf{L}}_{\mathbf{gl}}$ are properly transformed in the sensor spectral domain accounting for the TASI sensor specifications [1]. We obtained the noisy ground-leaving radiances considering a Gaussian additive noise with zero mean and diagonal covariance matrix. The noise has been simulated as suggested in [2]. To give an example, in our experiments we compare the performance for Noise Equivalent Delta Temperature (NEDT) equals to 0K (noise-free radiance), and NEDT = $0.1$K (moderate noise level). To discuss the results, we use the Receiver Operating Characteristics (ROC) curves. Specifically, we generated M realizations of ${\mathbf{L}}_{\mathbf{gl}}$ for both the TOI and the "background", by simulating M different sets of noise vectors for each selected value of NEDT, and M different sets of integrated water vapor values w, to simulate the ${\mathbf{L}}_{\downarrow }$ variability. The values of w are extracted from a uniform distribution within the interval $\left[0.5-3.5\right]gr/c{m}^2$. The algorithm proposed in Equation (3) is then applied to each set of noisy radiances to obtain the detection statistic. The presence of the TOI in the observed surface is declared if the statistic is lower than a given threshold. Instead, the surface is assigned to the class "background" if the statistic is higher than the threshold.

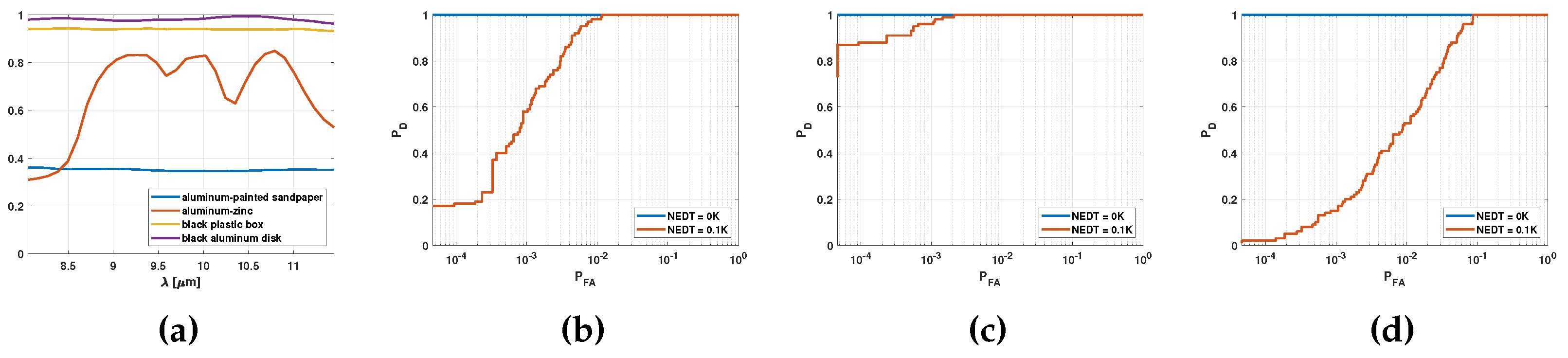
3. Results and Discussion

For this example, we consider the detection algorithm where the basis matrix $\mathbf{A}$ has a rank $K=3$.

Figure 1b, 1c, and 1d show the ROC curves for the evaluated materials: aluminum-painted sandpaper, black aluminum disk, and black plastic box. Since there were no false alarms, the ROC curve for aluminum-zinc is not shown. The spectral variability of the aluminum-zinc signature allows us to always detect the material against the simulated "background" spectra. At NEDT = 0K, the three materials can be always detected with respect to the simulated "background". At NEDT = 0.1K, as expected, the worse performance are obtained for the black plastic box, due to its completely flat spectral shape (Figure 1a). In fact, this feature makes the material spectral emissivity easy to confuse with some other spectrum. However, for probabiliy of false alarm ${\mathbf{P}}_{\mathbf{FA}}=5·{10}^{-2}$, black aluminum disk and aluminum-painted sandpaper feature a probability of detection ${\mathbf{P}}_{\mathbf{D}}=1$, and black plastic box ${\mathbf{P}}_{\mathbf{D}}\simeq 0.9$, proving the effectiveness of the proposed algorithm

4. Conclusions

In this paper, we have presented a new approach to target detection of materials with known spectral emissivity, in the framework of LWIR hyperspectral systems. The proposed method takes into account the spectral variability of the downwelling radiance by means of a subspace-based approach. The preliminary analysis, carried out with simulated data, has shown that the algorithm may robustly detect materials whose emissivity exhibits high spectral variability. Instead, detection performance with materials whose emissivity has low spectral variability, is sensibly affected by the noise level. Future work will be focused on extending the analysis to a larger set of surface spectral emissivities, and the application of the technique to a real hyperspectral image.