Abstract
In the last decade, surface-enhanced Raman spectroscopy (SERS) met increasing interest in the detection of chemical and biological agents due to its rapid performance and ultra-sensitive features. SERS is a combination of Raman spectroscopy and nanotechnology; it includes the advantages of Raman spectroscopy, providing rapid spectra collection, small sample sizes, and characteristic spectral fingerprints for specific analytes. In this paper, we detected label-free SERS signals for arbitrarily configurations of dimers, trimers, etc., composed of gold nanoshells (AuNSs) and applied to the mapping of osteosarcoma intracellular components.
1. Introduction
Raman spectroscopy is a vibrational spectroscopic technique able to identify molecular species in a wide range of analytical applications [1]. One critical aspect of Raman spectroscopy is its relatively weak signals. Consequently, in the last decades, methods for enhancing the signal have been developed in order to enable the detection of small quantities of analytes [2,3,4]. The most efficient method to enhance the Raman signal involves the plasmonic confinement of electromagnetic fields due to metal nanorough surfaces [5]. This method takes the name surface-enhanced Raman spectroscopy (SERS). The strong Raman signal, generated by the SERS effect, enables short acquisition times consistent with the general requirements for both higher-throughput analysis and biological sampling and imaging. When a molecule is located between two metallic nanoparticles (NPs), for example, both the fluorescence and the Raman cross section are much larger than for a molecule far from the metallic NPs. The enhancement factor is generally composed of two contributions: one is the electric field enhancement factor, Γ(ω) = |E|2/|E0|2 (where E0 is the incident electric field and E the electric field scattered at the position of the molecule). The other one is the enhancement factor, Γm, that measure of how much the decay rate of an excited state of the molecule is enhanced near the metallic nanoparticles.
In this paper, we introduce numerical SERS enhancement maps depending on the arrangement of AuNSs internalized in the upper layers of the hosting cells. We demonstrate that in complex environments like inner mammalian cells, when the spatial maps of the SERS enhancement are known, it is possible to have a reasonable estimation on the average number of molecules in the scattering volume of the SERS active areas defined by the AuNSs clusters. Although preliminary and qualitative, the advantages of our results in the application of SERS spectroscopy in biology and oncology are straightforwardly understandable.
2. Green’s Function Description of SERS Effect Generated by AuNSs
The main features of SERS spectroscopy lie in its ability to enhance the electromagnetic signal stimulated by the hotspots in nanostructured metals. The enhancement factor can be defined as the ratio of SERS signal to the Raman signal that would be obtained for the same substance in the absence of the SERS substrate, with all the other conditions being similar. An operative definition of SERS enhancement is, hence, EF = (ISERS/Nsurf)/(IRS/Nvol), where ISERS is the SERS intensity, IRS the intensity for non-SERS Raman measurement. A more accurate definition of the Raman scattering molecules requires that Nsurf be the number of molecules located in the hotspot region, typically confined to a surface rather than a volume, and Nvol is the average number of molecules in the scattering volume involved in the non-SERS Raman measurements. This definition of enhancement factor requires that the number of molecules inside the hotspots is accurately determined. Since an accurate determination of the number of subcellular components is currently not possible, our approach is to determine precisely the enhancement factor and its spatial distribution. The critical question on the complete knowledge of the electric field, and hence of the enhancement factor, can be addressed in the quantification of the Green function of the metal–insulator–metal (MIM) system composed by two or more AuNSs close one each other. To do this, consider N identical dipolar spherical AuNSs of total radius R, polarizability α, located at the positions ri and an incident monochromatic light characterized by a complex electric-field amplitude E0(r, ω). The size of the AuNSs is supposed to be small compared to the wavelength of the incoming light and, for sake of simplicity, the electric permeability and the polarizability of the AuNSs are assumed isotropic. The detected intensity is proportional to the spectral density that is averaged square modulus of the electric field, i.e., , being the detector located at r0, so that the problem consists in calculating the electric field amplitude at each particle position i. Since all the AuNSs are in mutual interaction one each other, the problem is self-consistent and Green’s dyadic tensor formalism is the best choice to solve the problem. The mutual external electric field is expressed by the relation
where G is the Green dyadic function of the complete system. The second components in Equation (1) is given by the dyadic Green’s function that accounts, among other factors, the atomic roughness in the MIM cavity. For a system of random localized AuNSs, the Green function reads [4]
where denotes the Hankel function of first kind and order zero, εm(ω) represents the metal electric permittivity described by the Drude model Equation (2), kr is a spatial wavevector being the root of Θ(kr) + 1 = 0 (where Θ is a function linking the reflection coefficient to spectral density and plasmon wavevector, see [5]), in turn, δ is a numerical factor. The singularities in Equation (2) correspond to the eigenmodes driving the plasmon resonance and the field enhancements. This is because the pole accounts for all the most relevant contributions to Green’s functions from the random rough surface.
The non-linear nature of Equation (2) implies the advantage to have spatially narrow electromagnetic enhancements, narrower, in particular, of laser-beam spot size. This property results in a super-resolution SERS effect able to discriminate, as we will show, single intracellular components.
The next section presents some significant experimental results and the corresponding numerical evaluation using the Equations (1) and (2).
3. Results
The experimental study was focused to exploit local enhanced fields generated by AuNSs in osteosarcoma cells for identifying biochemical components characterizing the cancer cells. Before application of SERS, Raman spectroscopy and imaging were carried out on osteo-differentiated MSCs and osteosarcoma cells with the aim of discriminating between the different the cell populations. The ability to discriminate between osteo-differentiated MScs and osteosarcoma cells consists in identifying the major biochemical components characterizing osteosarcoma cells. Hence, in the second experimental stage, SERS was applied to osteosarcoma cells with the aim of understanding if and how local fields generated by the AuNSs (previously internalized in the MG-63 cells) enhance the biochemical components characterizing the osteosarcoma cells.
Analogously to a Raman imaging map, also SERS map can be regarded as a matrix X of dimension m by n, where the Raman spectrum of each recorded position correspond to a row vector, the spectra modified by SERS effect can be linked to spatial hotspots. Figure 1 summarizes the main results obtained, which include the SERS effect as measured and simulated. Details on simulated spectra can be found in [5].
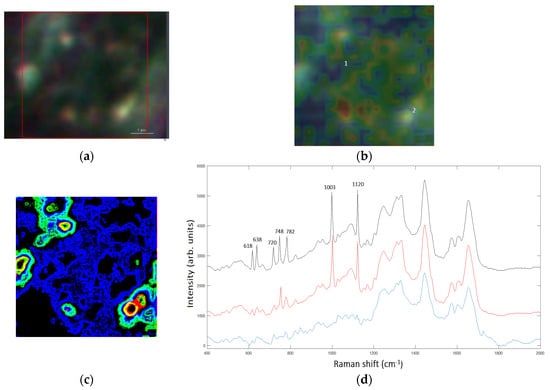
Figure 1.
(a) Denotes the bright-field image of MG-63 nuclear area where the bright points display the AuNSs, scale bar 1 μm, (b) represents the correspondent Raman map of the area marked by the red box in (a). The labels 1 and 2 mark a non-SERS and a SERS domain characterized by the AuNSs dimer. (c) Shows the Raman map calculated with Green’s function: the red regions denotes the spatial areas with Γ2~105. (d) Displays the Raman spectra in the recorded Raman map, label 1 (blue line), label 2 (red line) and in 2 after data processed with simulated map (c), black line.
Raman spectroscopy, amplified by SERS AuNSs can provide imaging modality including high molecular specificity, high sensitivity, and negligible autofluorescence. The absorption of nanoparticles by the cells via endocytosis allows exploitation of the hotspots generated by the plasmonic properties of the NPs to perform internal spectroscopy of the cells themselves and to discriminate between healthy- and tumor cells. In this paper, firstly, experimental measurements were carried out on osteo-differentiated MSCs and osteosarcoma cells with standard Raman spectroscopy, respectively. Hence, we have focused on the numerical quantification of subcellular components of osteosarcoma cells, by using the SERS signals exploiting the AuNSs internalized in the MG-63 cells. The local SERS signal is simulated by Equations (1) and (2). In Figure 1, it is shown that the biochemical components characterizing osteosarcoma cells, such as DNA (Raman band at 618, 638, 748 and 782 cm−1), Phe (Raman band at 1003 cm−1), or β-carotene (Raman band at 1120 cm−1) can be obtained by local SERS mapping. In addition, local SERS signals reveal new enhanced components providing a local spectroscopy analysis that can elucidate the biochemical transformations of cancer cells, such as specific amino acids in their connection to the metabolism of cancer cell, or β-carotene in connection to the apoptosis mechanism of elimination of neoplastic cells.
The methodology presented in this paper is general, requiring only an accurate experimental knowledge of the distribution of metallic nanoparticles and can be applied to all SERS methodologies in oncology.
Author Contributions
M.D. developed the theoretical model, conceived the experiment, performed the measurements, interpreted the data and wrote the article.
Funding
This research received external funding out within the framework of the BIO-ICT joint laboratory between the Institute of Biophysics and the Institute of Information Science and Technologies, both of the National Research Council of Italy, in Pisa.
Acknowledgments
The author likes to acknowledge Serena Danti, Luisa Trombi, Delfo D’Alessandro, and University of Pisa, for the preparation of cell samples.
Conflicts of Interest
The author declares no conflict of interest.
References
- Smith, E.; Dent, G. Modern Raman Spectroscopy-A Practical Approach; John Wiley & Sons: Chichester, UK, 2005; ISBN 0-471-49668-5. [Google Scholar]
- Le Ru, E.C.; Etchegoin, P.G. SERS enhancement factors and related topics. In Principles of Surface Raman Spectroscopy; Le Ru and Etchegoin, Eds; Elsevier: Amsterdam, The Netherlands, 2009; pp. 185–264. [Google Scholar] [CrossRef]
- Cialla-May, D.; Zheng, X.-S.; Weber, K.; Popp, J. Recent Progress in surface-enhanced Raman spectroscopy for biological and biomedical applications: From cells to clinics. Chem Soc. Rev. 2017, 46, 3945–3961. [Google Scholar] [CrossRef] [PubMed]
- D’Acunto, M. Detection of Intracellular Gold Nanoparticles: An Overview. Materials 2018, 11, 882. [Google Scholar] [CrossRef] [PubMed]
- D’Acunto, M. In situ Surface-Enhanced Raman Spectroscopy of cellular components. Theory and experimental results. Materials 2019, 12, 1564. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).