3D Shape Measurement Based on Digital Speckle Projection and Spatio-Temporal Correlation ^†

Abstract

With the non-periodicity and discrete nature, and unnecessary of phase unwrapping process, digital speckle correlation method shows its significant advantages in three-dimensional (3D) shape measurement. Combining with the spatial correlation and temporal correlation method in the digital speckle correlation, a spatio-temporal digital speckle correlation was developed in this paper, which can improve the accuracy of 3D shape measurement and effectively reduce the number of the recorded speckle images for restoring the corresponding 3D shape at the same time. In the experiment, only 5 frames of the required speckle images was needed to reconstruct the 3D shape of a complex object with spatio-temporal digital speckle correlation method, and its accuracy was same as the result when 20 frames speckle images were used in temporal correlation method.

1. Introduction

Digital Speckle Correlation Method (DSCM) is an optical three-dimensional (3D) measurement method. This method takes the speckle’s gray value as the carrier for the 3D information of a measured object. The essential point of DSCM is to get the whole-field distribution of displacement and strain by studying the distribution of the digital gray field of the object before and after its deformation. This method has many advantages compared with traditional 3D shape measurement method, such as non-contact and full-field measurement, simply structured, white light illumination, low environmental requirements, adjustable measuring range, simple data collection, easy to realize automation, without phase unwrapping process, etc.

At the beginning of the 80s of last century, I. Yamaguchi [1], W. H. Peters and W.F. Ranson [2] proposed DSCM technology independently. In 1982, I. Yamaguchi used DSCM to measure 2D steady laminar flow for the first time. W. H. Peters and W. F. Ranson used DSCMto determine the dynamic parameters of the rigid body (angular velocity and linear velocity) in the same year. In 2001 and 2002, Guanchang Jin brought wavelet denoising algorithm and 2D discrete orthogonal wavelet into digital speckle correlation operation process for the purpose of eliminating the influences from high frequency noise, and improving the operation speed and the measurement accuracy of the displacement field increased to 0.01~0.005 pixels [3,4]. The application of DSCM in the field of 3D shape measurement had also made some progress. In 1990, Kahn-Jetter Z. L. and T. C. Chu [5] combined DSCM with stereo vision principle, and completed the deformation test of a bending cantilever, the displacement test of a planar surface and a elliptical ring. In 2001, Dai Hongjun and Su Xianyu [6,7] proposed the digital speckle temporal sequence correlation method. In their further works, multi correlation peaks optimization method is used to improve the measurement accuracy of method [8], and the fast local search algorithm is help to speed up the computational process. In 2010, Pan Bing proposed an average grayscale gradient [9] for the quality evaluation of actual speckle patterns. In 2014, Junpeng Xue completed the system calibration of digital speckle temporal sequence correlation measurement with a auxiliary camera determined the horizontal world coordinates of the tested object [10]. In 2015, Junpeng Xue adopted the digital speckle correlation method based on color speckle pattern projection to realize the high speed 3D measurement of the human face [11].

Most of these scholars’ research on DSCM can be divided into spatial correlation or temporal correlation. Both of them have their own advantages and disadvantages. The digital speckle spatial correlation method based on stereo vision has low accuracy, but this method only needs one pair of images synchronously shot by the left and right camera to complete the measurement process, which is suitable for the measurement of dynamic objects. The temporal correlation method has high accuracy, but the measurement process needs dozens of images, which is suitable for the measurement of static (quasi-static) objects. In this paper, a new spatio-temporal digital speckle correlation method is proposed, which combines the spatial correlation method with the temporal correlation method. The new method improves the accuracy of the spatial measurement, and also reduces the number of the temporal correlation effectively.

This paper is arranged as following, Section 2 explains the principles of the spatial correlation, temporal correlation and the new spatio-temporal digital speckle correlation method. Section 3 presents some experimental results of three digital speckle correlation methods and compares their accuracy. Section 4 concludes this paper.

2. Principle of Three Methods of Digital Speckle Correlation

Imitating the human eyes to observe objects, two cameras of a stereo vision system are used to get 2D images of the target from different directions. The parallax map is obtained by matching these information of two 2D images, and the 3D shape of the observed object can be reconstructed according to the calibration of two cameras’ parameters and their location relations.

The geometric model of a stereo vision system is shown in Figure 1. M is an arbitrary point on the measured object, M_l and M_r are the image spots on the left and right camera imaging plane. If the image coordinates of M_l and M_r are known, the parallax of M can be calculated with the system correlation results. Then the 3D shape of the measured object can be reconstructed according to the world coordinates of M. However, when there is no texture or feature point on the tested surface, it will be very difficult to match the corresponding points. In order to solve this problem, digital speckle projection method has been brought into the stereo vision system to encode the tested objectin spatial- or temporal-domain and help the homonymy points’ matching, known as digital speckle correlation measurement.

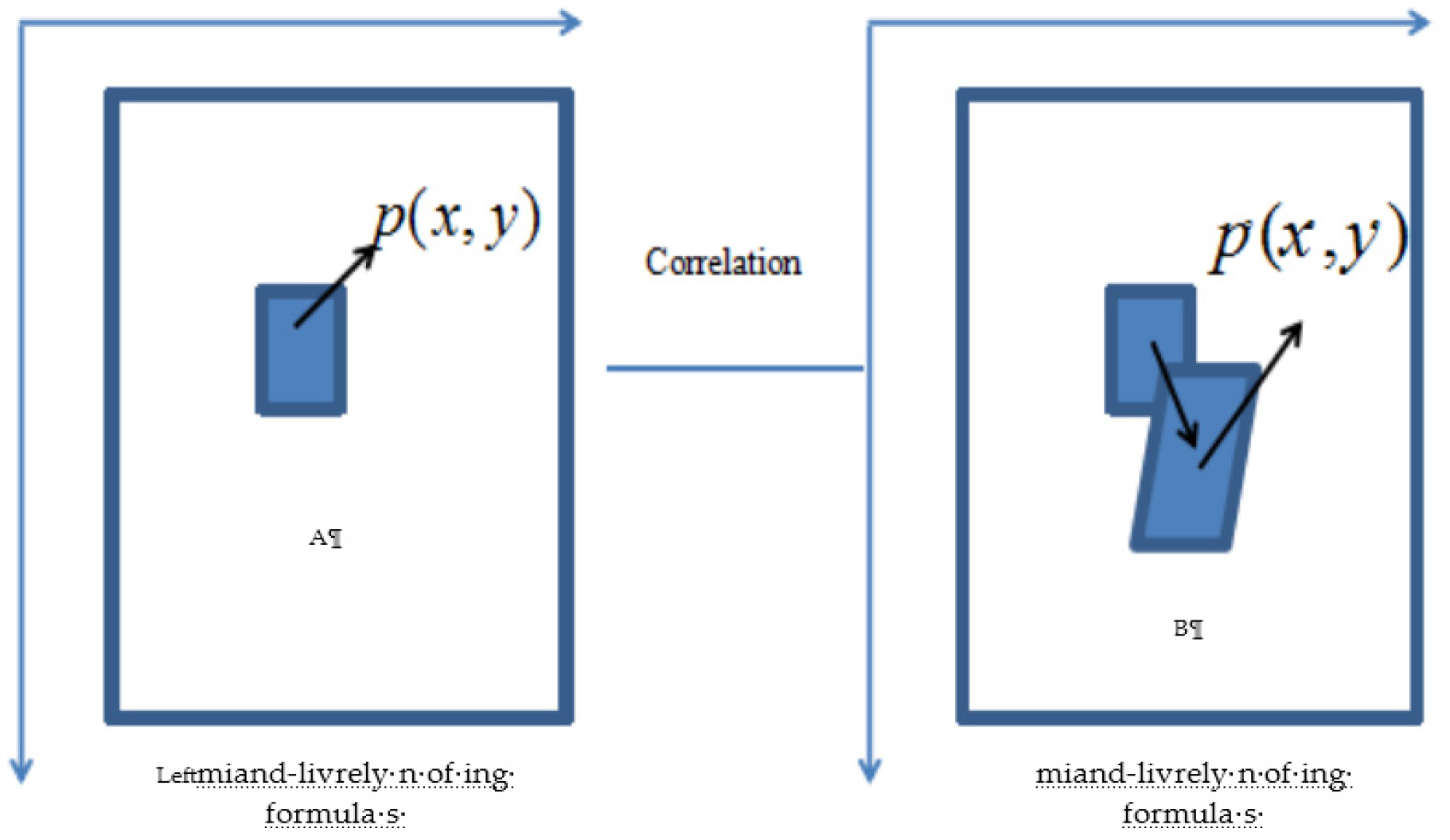
2.1. Principle of Digital Speckle Spatial Correlation

In the digital speckle spatial correlation method, the grayscale value of the projected random digital speckle pattern is a carrier of the tested object’s height distribution. The correlation calculation is carried out on two subimages chose from the left and right image respectively. The principle of digital speckle spatial correlation is shown in Figure 2. p is the center of the subimage A (with the size of (2m + 1) × (2m + 1) pixels) in the left speckle pattern, and the same size subimage B is chose from the right speckle pattern. The correlation value of two subimages A and B is calculated according to the principle of probability statistics. The Zero-Normalized Cross-Correlation (ZNCC) [7] is a common algorithm for the calculation of the correlation value C shown in the following formula

$$C=\frac{{\displaystyle {\sum }_{i=1}^m{\displaystyle {\sum }_{j=1}^m[(f(x_i,y_j)-\overline{f})\cdot (g(x_i^{\prime },y_j^{\prime })-\overline{g})]}}}{\sqrt{{\displaystyle {\sum }_{i=1}^m{\displaystyle {\sum }_{j=1}^m{(f(x_i,y_j)-\overline{f})}^2}}\cdot {\displaystyle {\sum }_{i=1}^m{\displaystyle {\sum }_{j=1}^m{(g(x_i^{\prime },y_j^{\prime })-\overline{g})}^2}}}}$$

(1)

In formula (1), f and g is the gray value of the left and right speckle patterns respectively,$\overline{f}\mathrm{and}\overline{g}$ is the average gray level of the two subimages. When the correlation value C equals 1, it is completely correlated; when the correlation value C equals 0, it is completely uncorrelated.

Once their correlation value reaches the maximum value (or the smallest one), A and B are labeled as the matching areas and the central position of B can be determined by the peak of the correlation function. Their parallax information will be finally used to reconstruct the 3D shape of the tested object. In short, the digital speckle spatial correlation method realizes the extraction of parallax and reconstructs the 3D shape of the object by finding the corresponding matching points one by one through the correlation operation in 2D spatial domain.

2.2. Principle of Digital Speckle Temporal Correlation

From the principle of digital speckle spatial correlation, it is found that the matching point is located by matching the left and right speckle patterns in 2D spatial domain. It has its obvious advantage that only one pair of digital speckle pattern is need to restored the 3D shape information. But its reconstruction accuracy is lower. So, some scholars have proposed digital speckle temporal correlation method in order to improve the accuracy of DSCM [12]. This method obtains the matching points by doing the correlation calculation along the time axis.

The principle of digital speckle temporal correlation is shown in Figure 3, a projector projects a series of time-varying speckle patterns onto the surface of the measured object to encode the shape in temporal domain. p₁(x₁,y₁) is any point in image getting from camera 1, p₂(x₂,y₂) is any point from camera 2. The ZNCC formula is used to calculate the correlation value of these two points. If the value is maximum, the two points are matching points for each other.

$$\begin{array}{l}\rho (p_1,p_2)=\\ \frac{{\displaystyle {\sum }_{t=1}^N[g_1(x_1,y_1,t)-\overline{g_1(x_1,y_1,t)}]\cdot [g_2(x_2,y_2,t)-\overline{g_2(x_2,y_2,t)}]}}{\sqrt{{\displaystyle {\sum }_{t=1}^N{[g_1(x_1,y_1,t)-\overline{g_1(x_1,y_1,t)}]}^2}}\cdot \sqrt{{\displaystyle {\sum }_{t=1}^N{[g_2(x_2,y_2,t)-\overline{g_2(x_2,y_2,t)}]}^2}}}\end{array}$$

(2)

where, g₁(x₁,y₁,t) represents the gray value of p₁(x₁,y₁) in the image recorded at t time by camera 1.$\overline{{\mathrm{g}}_1\left(x_1,y_1,t\right)}$ is the time average gray value of p₁(x₁,y₁) on all N frame images recorded by camera 1. g₂(x₂,y₂,t) represents the gray value of p₂(x₂,y₂) in the image recorded at t time by camera 2. $\overline{{\mathrm{g}}_2\left(x_2,y_2,t\right)}$ is the time average gray value of p₂(x₂,y₂) on all N frame images recorded by camera 2.

2.3. Principle of Digital Speckle Spatio-Temporal Correlation

In the above two digital speckle correlation methods, spatial correlation method only needs one speckle pattern to reconstruct the 3D shape of objects, but the accuracy is low. The temporal correlation method has high accuracy, but more speckle patterns are needed. For improving the accuracy of spatial measurement and reducing the image number of the speckle patterns of temporal correlation method, spatio-temporal correlation operations is helpful and has been used in DSCM. The principle of digital speckle spatio-temporal correlation method is shown in Figure 4.

A series of time-varying speckle patterns are projected onto the surface of the measured object, and two cameras in the stereo vision system shot the speckle patterns synchronously. Takingp₁,one matching point in the left image, as the center, a region Ω with the width of s_x, length of s_y and depth of s_t on temporal domain along the sampling time axis is formed. The same size speckle volume from camera 2 is chose to do the spatio-temporal correlation operation with the speckle volume around p₁.

$$\rho (p_1,p_2)={\displaystyle \sum _{i,j,k\in \Omega }{w}_{ijk}(p_1,t_0)\times \frac{I_1^{ijk}(p_1,t_0)-M_1(p_1,t_0)}{\sqrt{V_1(p_1,t_0)}}\times \frac{I_2^{ijk}(p_2,t_0)-M_2(p_2,t_0)}{\sqrt{V_2(p_2,t_0)}}}$$

(3)

Ω is the spatio-temporal correlation area. And the value of i, j and k is shown in the following formula (4):

$$i,j,k=-\frac{s_{x,y,t}-1}{2},-\frac{s_{x,y,t}-1}{2}+1,\dots ,\frac{s_{x,y,t}-1}{2}$$

(4)

Usually, s_x, s_y and s_t are odd.

${\mathrm{I}}_{\mathrm{a}}^{\mathrm{ijk}}\left({\mathrm{p}}_{\mathrm{a}},{\mathrm{t}}_0\right)$ is the gray value of p_a (a=1,2) in t₀ frame, ${\mathrm{M}}_{\mathrm{a}}({\mathrm{p}}_{\mathrm{a}},{\mathrm{t}}_0$) is the mean value of the spatio-temporal correlation area,${\mathrm{V}}_{\mathrm{a}}({\mathrm{p}}_{\mathrm{a}},{\mathrm{t}}_0$) is the variance of the spatio-temporal correlation area. Their specific calculation process is shown in the following formula (5).

$$\{\begin{array}{c}{I}_a^{ijk}(p_a,t_0)=I_a^{}(x_a+i,y_a+j,t_0+k)\\ M_a(p_a,t_0)={\displaystyle \sum _{i,j,k\in \Omega }{w}_{ijk}(p_1,t_0)I_a^{ijk}(p_a,t_0)}\\ V_a(p_1,t_0)={\displaystyle \sum _{i,j,k\in \Omega }{w}_{ijk}(p_1,t_0)\times {[I_a^{ijk}(p_a,t_0)-M_a(p_a,t_0)]}^2}\end{array}$$

(5)

Comparing with the spatial correlation and temporal correlation, the spatio-temporal correlation method is mainly improved in the weight factor w_ijk. And this weight factor w_ijk has its normalized property. In our research work, w_ijk = 1/(s_x·s_y·s_t).

After doing the spatio-temporal correlation and searching for the maximum value of correlation curves, the matching points of the left and right speckle patterns can be obtained, then the parallax map can also be calculated according to the calibrated external parameters and internal parameters of the stereo vision system, so that the 3D shape of a object can be reconstructed.

3. Experimental Results

The experimental setup has been established for principle-proof and is shown in Figure 5. The employed cameras are German IDS UI-1240SE-M-GL, with the resolution of 1280 × 1024 pixels and 12 mm focal length lens. The projector is developed on DMD-based DLP4500 chip, whose resolution is 1280 × 800 pixels. To form a changing speckle pattern, the projector moved at 1 mm intervals along the baseline of the stereo vision driven by a linear translation platform. So, tens of frame digital speckle were projected onto the surface of the measured object and synchronously recorded by two cameras. A relief of the petal model has been taken as a measured object in first experiment. Figure 6 show one pair of speckle patterns which two cameras captured synchronously at a certain time.

Totally, 20 frames speckle patterns have been recorded by each camera. In digital spatial correlation method, the window size of speckle is 9 × 9 pixels, and only one frame pattern from each camera was used to do spatial correlation, which parallax map is shown in Figure 7a. In digital temporal correlation method, the window size (s_x, s_y) of speckle is also 9 × 9 pixels, and all 20 frames pattern (N = 20) from each camera were used to do temporal correlation, which parallax map is shown in Figure 7b. In digital spatio-temporal correlation method, the window size (s_x, s_y) of speckle is also9 × 9 pixels, and only 5 frames pattern (s_t = 5) from each camera were used to do spatio-temporal correlation, which parallax map is shown in Figure 7c.

In Figure 7. the invalid value marked with white color are caused by the inherent shadow of triangulation and the effect of region mismatch. In Figure 7a, the invalid point in the edge of the petal model is the mismatching which caused by the height mutation of the flower. And the spatial correlation window makes the high frequency information of the petal model smoothed. It can be seen from Figure 7b that the petal model is more detailed, the parallax information on the edge is better than that of the spatial correlation method, and the number of invalid points which produced by mismatching is less. For the third method, digital speckle spatio-temporal correlation, only 5 frame speckle patterns need to reconstruct the 3D shape of the petal model, and the parallax information on the edge of the flower is significantly more detailed compared with the result of the digital speckle spatial correlation operation.

In order to evaluate the accuracy of the three correlation methods, a precision machined standard step-like workpiece with step height of 20 mm and a high precision ceramic plane are measured in this second experiment. Figure 8 shows the speckle pattern of the measured step-like workpiece. Figure 9 show the results of three methods. Figure 10 shows the height distribution on the cross section of step-like workpiece measured by three methods.

The average step height of most points is 19.78 mm measured by the spatial correlation method, 19.85 mm by the temporal correlation method, and 19.81 mm by the spatio-temporal correlation method.

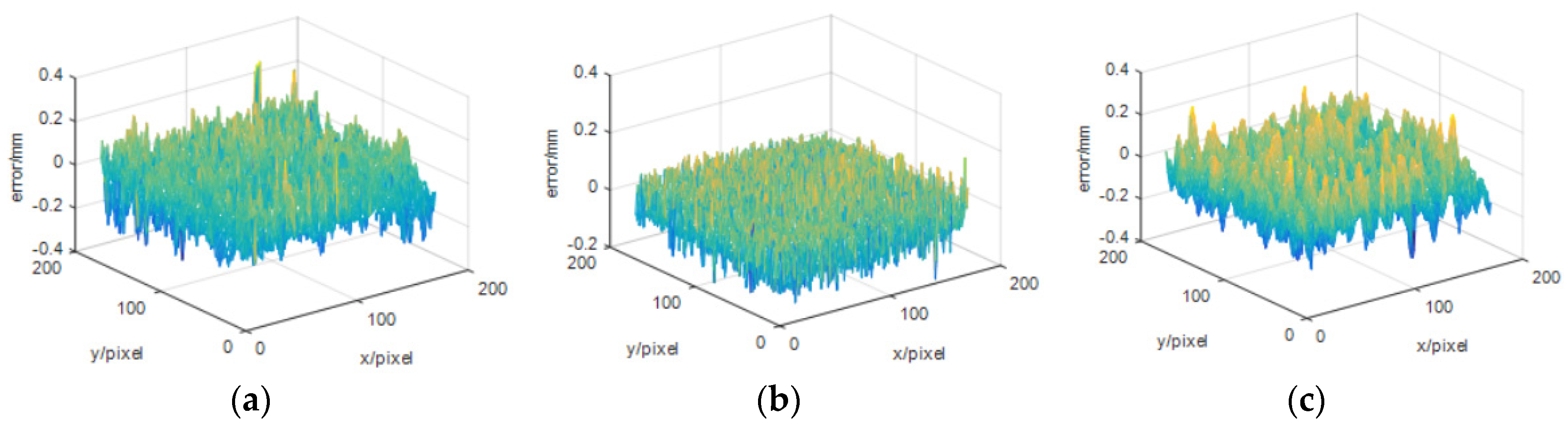
For the testing of the high precision ceramic plane, the correlation window in X- and Y-direction of three methods is 7 × 7 pixels. In temporal domain, the temporal correlation method involved all 20 frames speckle pattern, but the spatio-temporal correlation method only used 5 frames speckle pattern to restore the corresponding 3D shape. Figure 10 shows the height difference distribution between the plane restored by three speckle correlation methods and the fitted plane. And the standard deviation of three methods is 0.069 mm, 0.041 mm and 0.068 mm respectively.

From the results of second experiment, we can see that the accuracy of spatio-temporal correlation method is between that of spatial correlation and temporal correlation. But its required number of speckle patterns is less than temporal correlation method. Therefore, spatio-temporal correlation method is simple and effective.

In addition, we made further analysis on the relationship between the number of speckle images and the accuracy of reconstruction results in spatio-temporal correlation method.

Table 1. Relation between the measuring accuracy and the number of speckle image.

Description	Numerical Value
Number of speckle images (frame)	3	4	5	6	7	8	9	10
Standard deviation (mm)	0.0686	0.0683	0.0683	0.0551	0.0523	0.0473	0.0479	0.0452

lists the standard deviations of the reconstruction results of the standard plane by using different numbers of speckle images. From the table, it can be seen that the measuring accuracy presents a growth trend with the increasing number of the speckle images. But this growth is not linear change, when the number of speckle pattern reaches a certain value, the growth of the accuracy is slow down, that is to say, although the image number continues to increase, the benefits of accuracy won’t increase obviously any more. In actual measurement, the number of speckle images in spatio-temporal correlation is related to the complexity of objects. When the object’s surface is relatively simple, the number of speckle images can be reduced. But for measuring a complex shape, the reconstruction accuracy is sensitive to the number of speckle images.

4. Conclusions

On the basis of two existing methods, spatial correlation and temporal correlation method of digital speckle correlation measurement, a new method is proposed in this paper. The new method combines two methods to execute a spatio-temporal correlation to reconstruct the 3D shape of the measured objects. The corresponding reconstruction accuracy of three correlation methods is compared by actual experiments, the results show that the spatial correlation only needs one frame image for further reconstruction, which is suitable for measuring the dynamic object, but the accuracy is relatively low. The temporal correlation method needs to synchronously acquire dozens of speckle patterns, its accuracy is higher than that of the spatial correlation, which is suitable for measuring the static (or quasi static) object. The spatio-temporal correlation method presented in this paper is simple and effective, which can output the dense parallax map to restore 3D shape of the measured object. Above all, the number of the required speckle patterns of this method is effectively reduced from dozens to 4 or 5 while keeping the reconstruction accuracy is relatively high.