Sensitivity Analysis of Fiber-Matrix Interface Parameters in an SMC Composite Damage Model ^†

Abstract

This contribution shortly introduces the anisotropic, micromechanical damage model for sheet molding compound (SMC) composites presented in the authors’ previous publication [1]. As the considered material is a thermoset matrix reinforced with long (≈25 mm) glass fibers, the leading damage mechanisms are matrix micro-cracking and fiber-matrix interface debonding. Those mechanisms are modeled on the microscale and within a Mori-Tanaka homogenization framework. The model can account for arbitrary fiber orientation distributions. Matrix damage is considered as an isotropic stiffness degradation. Interface debonding is modeled via a Weibull interface strength distribution and the inhomogeneous stress distribution on the lateral fiber surface. Hereby, three independent parameters are introduced, that describe the interface strength and damage behavior, respectively. Due to the high non-linearity of the model, the influence of these parameters is not entirely clear. Therefore, the focus of this contribution lies on the variation and discussion of the above mentioned interface parameters.

1. Introduction

Sheet molding compound (SMC) composites receive increasing attention in industrial applications due to their high geometric freedom and low cycle times in manufacturing processes. In order to apply SMC composites, possibly locally reinforced with continuous fiber reinforced composites, as structural components, their mechanical and especially damage behavior must be examined and understood. Consequently, a precise and efficient prediction of the inhomogeneous, anisotropic and process-dependent mechanical properties can help to reduce the costly prototyping and further reduce development cycles. Various publications, therefore, are dedicated to the investigation of long fiber reinforced composites, such as SMC. Meraghni and Benzeggagh [2] and others [3,4,5], e.g., investigated damage propagation in randomly oriented, discontinuous fiber reinforced composites. Interface strength, using pull-out, push-out or fragmentation tests was characterized by, e.g., Favre et al. and others [6,7]. Jendli et al. [3] and others [5,8] investigated the influence of the strain rate on the mechanical and damage behavior. Based on the experimental findings, a variety of models have been developed. Yang et al. [9] proposed a phenomenological damage model that is able to depict a transversely isotropic stiffness degradation. Various one- or two-step homogenization approaches are based on replacing a fiber with a damaged interface by an equivalent fiber with an undamaged interface (see, e.g., [10,11,12,13]). Hereby, either the localization tensor or the Eshelby tensor need to be computed numerically. Other approaches as, e.g., Ju and Lee [14,15] consider fibers with damaged interfaces as either matrix material or voids. Interface debonding is commonly driven by a combination of the local shear and normal stress on the interface [10,16]. Depending on the considered material combination plastic effects [13,14] or viscous effects [4,14] are taken into account. Despite the enormous work already conducted within the research of discontinuous fiber reinforced composites, some deficiencies still remain open. Few models, e.g., are physically motivated, take the microstructure into account and are still able to calculate structural components in reasonable time. Phenomenological models often use a variety of parameters, which cannot always be interpreted meaningfully. The model presented here addresses such deficiencies. Due to an efficient damage algorithm and rigorous numerical regularization the physical model is applicable to large scale problems. The Weibull based interface characterization comes with only three independent parameters. In this contribution the interface parameters and their influence on the damage evolution and overall stress-strain relation are studied.

2. Continuum Mechanical Model

2.1. Fundamentals

According to [1] the SMC composite is considered a two-phase composite consisting of a matrix phase with volume fraction $c_{\mathrm{M}}$ and glass fibers with volume fraction $c_{\mathrm{F}}=1-c_{\mathrm{M}}$. The matrix and fibers are modeled linear elastic with isotropic stiffnesses ${ℂ}_{\mathrm{M}}$ and ${ℂ}_{\mathrm{F}}$, respectively. Furthermore, the fibers are modeled as straight ellipsoids with direction $\mathit{n}$, a uniform aspect ratio and a length of approximately 25 mm. Fiber bending and fiber breakage are neglected. The microscopic orientation of fibers within the composite can be specified by an empirical representation of the fiber orientation distribution function $f\left(\mathit{n}\right)$ (FODF) which is defined as

$$f\left(\mathit{n}\right)={\displaystyle \sum }_{\beta =1}^{K}c\left({\mathit{n}}_{\beta }\right)\delta \left(\mathit{n},{\mathit{n}}_{\beta }\right).$$

The weights $c\left({\mathit{n}}_{\beta }\right)$ are, so to speak, the volume fractions of fibers oriented in direction ${\mathit{n}}_{\beta }$ with respect to the total volume fraction $c_{\mathrm{F}}$, $\delta \left(\mathit{n},{\mathit{n}}_{\beta }\right)$ is the Dirac delta distribution and $K$ is number of considered directions. The weights $c\left({\mathit{n}}_{\beta }\right)$ are non-negative, normalized, and symmetric.

$$c\left({\mathit{n}}_{\beta }\right)\ge 0,\hspace{1em}\hspace{1em} {\displaystyle \sum }_{\beta =1}^{K}c\left({\mathit{n}}_{\beta }\right)=1,\hspace{1em}\hspace{1em} c\left({\mathit{n}}_{\beta }\right)=c\left(-{\mathit{n}}_{\beta }\right).$$

2.2. Effective Behavior

The relation between the macroscopic stress $\overline{\mathbf{\sigma }}$ and strain $\overline{\mathbf{\epsilon }}$ is given by the macroscopic stiffness $\overline{ℂ}$ as $\overline{\mathbf{\sigma }}=\overline{ℂ}\left[\overline{\mathbf{\epsilon }}\right].$Based on the Mori-Tanaka assumption that the fiber strain localization is calculated from the phase-averaged matrix strain ${\mathbf{\epsilon }}_{\mathrm{M}}$, the effective stiffness has the form (see [17])

$$\overline{ℂ}={ℂ}_{\mathrm{M}}-c_{\mathrm{F}}{(c_{\mathrm{M}}\langle {({\mathbb{P}}_0+{({ℂ}_{\mathrm{F}}-{ℂ}_{\mathrm{M}})}^{-1})}^{-1}{\rangle }_{\mathrm{F}}^{-1}+c_{\mathrm{F}}{({ℂ}_{\mathrm{F}}-{ℂ}_{\mathrm{M}})}^{-1})}^{-1}$$

Based on the Eshelby tensor ${\mathbb{E}}_0$, an explicit expression of the polarization tensor ${\mathbb{P}}_0={\mathbb{E}}_0{ℂ}_{\mathrm{M}}^{-1}$ can be found in Ponte Castañeda and Suquet [18]. Based on the empirical FODF, the fiber orientation average can be calculated using the Rayleigh product as

$${\langle \mathbb{A}\rangle }_{\mathrm{F}}={\displaystyle \sum }_{\beta =1}^K{c}_{\beta }\mathit{Q}\left({\mathit{n}}_{\beta }\right)\star {\mathbb{A}}_0$$

Hereby, ${\mathbb{A}}_0=\mathbb{A}\left({\mathit{e}}_1\right)$ is an arbitrary tensor in the reference orientation ${\mathit{e}}_1$ and $\mathit{Q}\left({\mathit{n}}_{\beta }\right)$ is a proper orthogonal rotation tensor. The Rayleigh product between such tensors is defined as $\mathit{Q}\star \mathbb{A}=A_{ijkl}\left(\mathit{Q}{\mathit{e}}_i\right)\otimes \left(\mathit{Q}{\mathit{e}}_j\right)\otimes \left(\mathit{Q}{\mathit{e}}_k\right)\otimes \left(\mathit{Q}{\mathit{e}}_l\right)$. The localized phase-averaged matrix and fiber stresses ${\mathbf{\sigma }}_{\mathrm{M}}$ and ${\mathbf{\sigma }}_{\mathrm{F}}$ can be calculated via the corresponding Mori-Tanaka stress localization relations

$${\mathsf{\sigma }}_{\mathrm{M}}={\mathbb{B}}_{\mathrm{M}}^{\mathrm{MT}}\left[\overline{\mathbf{\sigma }}\right],\hspace{1em}\hspace{1em}{\mathsf{\sigma }}_F={\mathbb{B}}_{\mathrm{F}}^{\mathrm{MT}}\left[\overline{\mathbf{\sigma }}\right].$$

The matrix and fiber stress localizations are determined by

$${\mathbb{B}}_{\mathrm{M}}^{\mathrm{MT}}\left[\overline{\mathbf{\sigma }}\right]={\left(c_{\mathrm{M}}{\mathbb{I}}^{\mathrm{s}}+c_{\mathrm{F}}\langle {\mathbb{B}}_{\mathrm{F}0}^{\mathrm{SIP}}\rangle {}_{\mathrm{F}}\right)}^{-1},\hspace{1em}\hspace{1em} {\mathbb{B}}_{\mathrm{F}}^{\mathrm{MT}}=\langle {\mathbb{B}}_{\mathrm{F}0}^{\mathrm{SIP}}\rangle {}_{\mathrm{F}}{\mathbb{B}}_{\mathrm{M}}^{\mathrm{MT}}$$

Hereby, the fiber stress localization tensor in the single inclusion problem (SIP) in the reference orientation ${\mathbb{B}}_{\mathrm{F}0}^{\mathrm{SIP}}$ is given by

$${\mathbb{B}}_{\mathrm{F}0}^{\mathrm{SIP}}={({\mathbb{I}}^{\mathrm{s}}+{ℂ}_{\mathrm{M}}\left({\mathbb{I}}^{\mathrm{s}}-{\mathbb{P}}_0{ℂ}_{\mathrm{M}}\right)\left({ℂ}_{\mathrm{F}}{}^{-1}-{ℂ}_{\mathrm{M}}{}^{-1}\right))}^{-1}$$

As shown by Duschlbauer et al. [19], the directional dependent fiber stress ${\mathsf{\sigma }}_{\mathrm{F}}^{\angle }\left(n_{\beta }\right)$ is calculated as

$${\mathsf{\sigma }}_{\mathrm{F}}^{\angle }\left(n_{\beta }\right)={\mathbb{B}}_{\mathrm{F}}^{\mathrm{SIP}\angle }\left({\mathit{n}}_{\beta }\right){\mathbb{B}}_{\mathrm{M}}^{\mathrm{MT}}\left[\overline{\mathbf{\sigma }}\right],\hspace{1em}\hspace{1em} {\mathbb{B}}_{\mathrm{F}}^{\mathrm{SIP}\angle }\left({\mathit{n}}_{\beta }\right)=Q\left({\mathit{n}}_{\beta }\right)\star {\mathbb{B}}_{\mathrm{F}0}^{\mathrm{SIP}}$$

2.3. Matrix Damage

Matrix damage is modeled as an isotropic degradation of the initial matrix stiffness ${ℂ}_{\mathrm{M}}^0$ via a scalar damage variable $d_{\mathrm{M}}$ as ${ℂ}_{\mathrm{M}}=\left(1-d_{\mathrm{M}}\right){ℂ}_{\mathrm{M}}^0.$ Since the thermoset matrix is considered brittle, the damage variable $d_{\mathrm{M}}$ is determined as a function of the maximal phase-averaged principal matrix stress

$$d_{\mathrm{M}}=d_{\mathrm{M}}\left(\underset{\mathsf{\tau }\in \left[0,t\right]}{\max }\left(\underset{\alpha =1,2,3}{\max }{\sigma }_{\mathrm{M}}^{\alpha }\right)\right)$$

Hereby, the outer $\max$ function ensures, that $d_{\mathrm{M}}$ can never decrease (e.g., healing is not possible).

2.4. Fiber-Matrix Interface Debonding

Due to the high aspect ratios, interface debonding is assumed to be driven by the stress on the lateral fiber surface. The stress vector $\mathit{t}$ on the said surface is given by $\mathit{t}\left({\mathit{n}}_{\beta },\mathit{s}\right)={\mathbf{\sigma }}_{\mathrm{F}}^{\angle }\left({\mathit{n}}_{\beta }\right)\left[\mathit{s}\right].$ Hereby, $\mathit{s}$ is the lateral surface normal of a fiber with direction ${\mathit{n}}_{\beta }$. The stress vector can be decomposed into its normal component ${\sigma }_{\mathrm{I}}$ in direction $\mathit{s}$ and shear component ${\mathsf{\tau }}_{\mathrm{I}}$ in direction $\mathit{m}$

$$\mathit{t}\left({\mathit{n}}_{\beta },\mathit{s}\right)={\sigma }_{\mathrm{I}}\left({\mathit{n}}_{\beta },\mathit{s}\right)\mathit{s}+{\tau }_{\mathrm{I}}\left({\mathit{n}}_{\beta },\mathit{s}\right)\mathit{m},\hspace{1em}\hspace{1em} \mathit{s}\perp {\mathit{n}}_{\beta }, \mathit{m}\perp \mathit{s}, {\tau }_1\left({\mathit{n}}_{\beta },\mathit{s}\right)\ge 0$$

The components are determined via projections of $\mathit{t}$ onto the corresponding directions

$${\sigma }_{\mathrm{I}}=\mathit{t}·\mathit{s},{\tau }_I=\sqrt{{\left(\mathit{t}·{\mathit{n}}_{\beta }\right)}^2+{\left(\mathit{t}·\left({\mathit{n}}_{\beta }\times \mathit{s}\right)\right)}^2}$$

In order to determine the interface damage, an equivalent interface stress ${\sigma }_{\mathrm{I},\mathrm{eq}}\left({\mathit{n}}_{\beta },\mathit{s}\right)$ is introduced

$${\sigma }_{\mathrm{I},\mathrm{eq}}\left({\mathit{n}}_{\beta },\mathit{s}\right)={\widehat{\sigma }}_{\mathrm{I},\mathrm{eq}}\sqrt[m]{{\left(\frac{{\tau }_{\mathrm{I}}\left({\mathit{n}}_{\beta },\mathit{s}\right)}{{\tau }_{\mathrm{I}0}}\right)}^m+{\left(\frac{\left\{{\sigma }_{\mathrm{I}}\left({\mathit{n}}_{\beta },\mathit{s}\right)\right\}}{{\sigma }_{\mathrm{I}0}}\right)}^m}$$

Three of the four parameters ${\widehat{\sigma }}_{\mathrm{I},\mathrm{eq}}$, ${\tau }_{\mathrm{I}0}$, ${\sigma }_{\mathrm{I}0}$ and $m$ are independent and will later be chosen according to literature values. The Macaulay bracket ensures that only non-negative normal stresses $\left\{{\sigma }_{\mathrm{I}}\left({\mathit{n}}_{\beta },\mathit{s}\right)\right\}$ contribute to the equivalent stress. Based on a weakest-link failure concept for the interface of a single fiber, a Weibull strength distribution for an inhomogeneous stress field is assumed [20]. This leads to a survival probability $P_{\mathrm{s}}\left({\mathit{n}}_{\beta }\right)$ of a fiber in direction ${\mathit{n}}_{\beta }$ of

$$P_{\mathrm{s}}\left({\mathit{n}}_{\beta }\right)=\exp \left(-\frac{1}{A_{\mathrm{I}0}}{{\displaystyle \int }}_{A_{\mathrm{I}}}{\left\{\frac{{\sigma }_{\mathrm{I},\mathrm{eq}}\left({\mathit{n}}_{\beta },\mathit{s}\right)-{\sigma }_{\mathrm{u}}}{{\sigma }_{\mathrm{o}}}\right\}}^k\mathrm{d}{A}_{\mathrm{I}}\right)$$

Here, $A_{\mathrm{I}}$ is the surface area of one fiber. The material parameters $A_{\mathrm{I}0}$, ${\sigma }_{\mathrm{u}}$, ${\sigma }_{\mathrm{o}}$ and $k$ characterize the fiber-matrix interface strength distribution. Again, the Macaulay-brackets $\{🞄\}=\max \left(0,🞄\right)$ ensure that the equivalent stress ${\sigma }_{\mathrm{I},\mathrm{eq}}$ only contributes above a certain threshold ${\sigma }_{\mathrm{u}}$. Analogously to the survival probability $P_{\mathrm{s}}\left({\mathit{n}}_{\beta }\right)$ a probability $P_{\mathrm{i}}\left({\mathit{n}}_{\beta }\right)$ of finding intact fibers in the corresponding direction ${\mathit{n}}_{\beta }$ needs to be calculated

$$P_{\mathrm{i}}\left({\mathit{n}}_{\beta }\right)=\frac{{\overline{c}}_{\beta }}{c_{\beta }^0},\hspace{1em}\hspace{1em} c_{\beta }^0>0$$

Hereby, the current fiber fraction $c_{\beta }={\overline{c}}_{\beta }+{č}_{\beta }$ is decomposed into an intact, load-carrying fraction ${\overline{c}}_{\beta }$ and a fraction of fibers with damaged interfaces ${č}_{\beta }$. The initial fiber fraction is $c_{\beta }^0$. The assumption of the presented interface damage model is that the probability $P_{\mathrm{i}}\left({\mathit{n}}_{\beta }\right)$ of finding intact fibers in a direction ${\mathit{n}}_{\beta }$ can never be higher than the probability $P_{\mathrm{s}}\left({\mathit{n}}_{\beta }\right)$ of fibers in that direction surviving a given external load. This leads to the consistency condition

$$\varphi \left({\mathit{n}}_{\beta }\right)=P_{\mathrm{i}}\left({\mathit{n}}_{\beta }\right)-P_{\mathrm{s}}\left({\mathit{n}}_{\beta }\right)\le 0$$

This direction-dependent damage function yields a natural evolution for the orientation distribution of intact, load-carrying fibers ${\overline{c}}_{\beta }$.

3. Fiber-Matrix Interface Parameters

Based on experimental findings according to [7,21], the interface parameters are chosen as ${\sigma }_{\mathrm{I}0}/{\tau }_{\mathrm{I}0}=1.5$ and $m=2$. Therefore, only three more parameters are independent. Following the survival probability $P_{\mathrm{s}}\left({\mathit{n}}_{\beta }\right)$ these independent parameters can be chosen as

$${\xi }_1≔{\sigma }_{\mathrm{u}},\hspace{1em}\hspace{1em}{\xi }_2≔\frac{1}{{\left(A_{\mathrm{I}0}\right)}^{1/k}}\frac{1}{{\sigma }_{\mathrm{o}}}{\widehat{\sigma }}_{I,\mathrm{eq}},{\hspace{1em}\hspace{1em}\mathsf{\xi }}_3≔k$$

The three parameters are estimated by fitting the material model to uniaxial tensile tests on bone specimens. ${\xi }_1$ is the lower stress threshold within the calculation of the survival probability $P_{\mathrm{s}}\left({\mathit{n}}_{\beta }\right)$, ${\xi }_2$ can be interpreted as a prefactor and ${\xi }_3$ is an exponent. In the following the parameters are varied from $25\%$ to $200\%$ according to the estimated values from the fitting procedure. Hereby, the effect on the macroscopic stress-strain relation under uniaxial tension and the corresponding evolution of the load-carrying fiber fraction $c_{\mathrm{F}}$ and matrix damage $d_{\mathrm{M}}$ are evaluated. Arrows indicate the influence of an increase of the parameters on the considered relations.

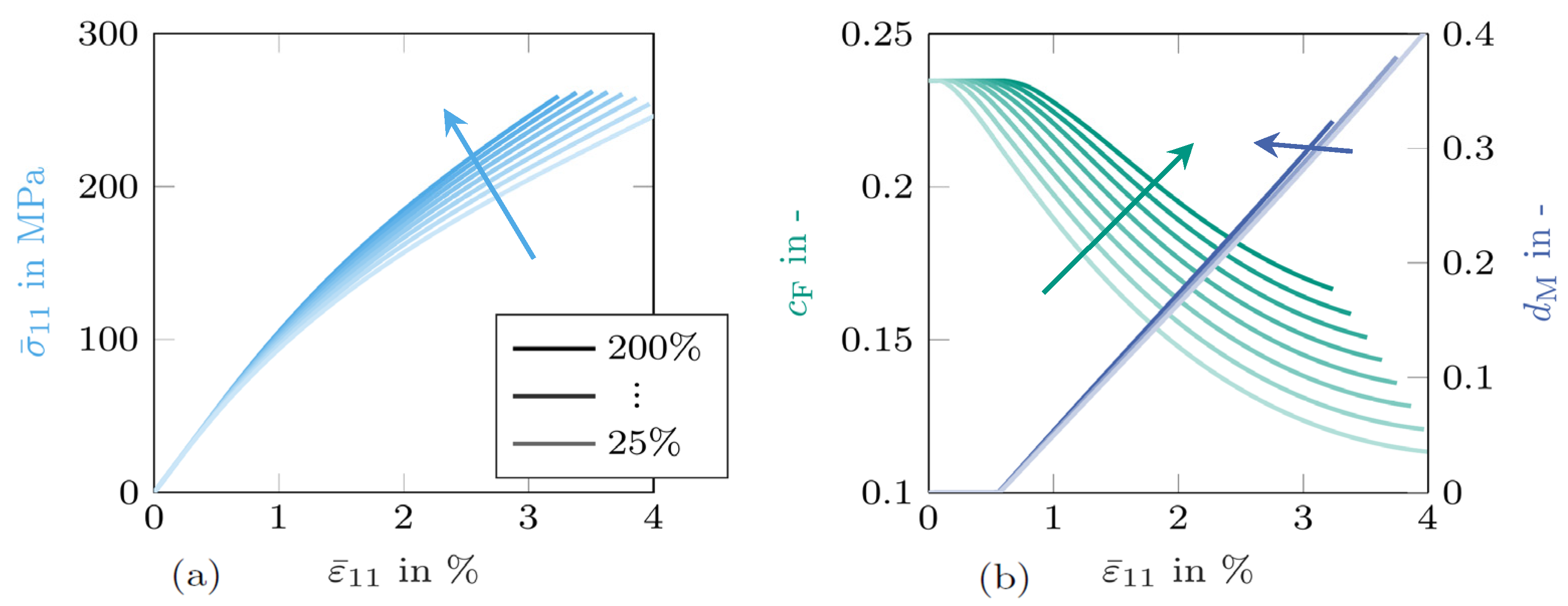
3.1. Variation of ${\xi }_1$

With an increase of the interface stress threshold ${\xi }_1$ the decrease of the load-carrying fiber fraction $c_{\mathrm{F}}$ is delayed (see Figure 1b). The equivalent interface stress, or the external load, respectively, needs to be higher in order to induce interface damage. That is to say, the fiber interfaces are stronger and can sustain a higher load. This means the interface strength is higher, if ${\xi }_1$ is higher, respectively. Accordingly, the overall stress-strain relation is stiffer, as can be seen in Figure 1a. The overall damage onset is delayed and weaker. Nevertheless, the evolution of the matrix damage (see Figure 1b) is hardly influenced and remains approximately the same for all tested variations of ${\xi }_1$. According to the model, the evolution of micro-cracks within the matrix is barely influenced by the lower interface damage threshold ${\xi }_1$.

3.2. Variation of ${\xi }_2$

An increase of the prefactor ${\xi }_2$ leads to an earlier and faster decrease of the load-carrying fiber fraction $c_{\mathrm{F}}$ (see Figure 2b). As the survival probability $P_{\mathrm{s}}\left({\mathit{n}}_{\beta }\right)$ according to Weibull is of the exponential type, a higher prefactor leads to a lower survival probability of a single interface. Similar to above, the influence of a change of ${\xi }_2$ on the matrix damage is quite little. But nevertheless, as the interface damage increases, the matrix damage $d_{\mathrm{M}}$ decreases accordingly. The overall stress-strain relation is softer for higher ${\xi }_2$. Damage onset is in total earlier and the damage evolution is faster.

3.3. Variation of ${\xi }_3$

The initiation of interface damage is not affected by a variation of the exponent ${\xi }_3$. But with an increase of ${\xi }_3$ the interface damage evolution is significantly slower. The relations are analogue to the ones described above for ${\xi }_2$. Due the exponential character of the Weibull survival probability $P_{\mathrm{s}}\left({\mathit{n}}_{\beta }\right)$, and the fact that the integral expression in this case is smaller than one, a higher exponent ${\xi }_3$ leads to a slower decrease of the load-carrying fiber fraction. Hereby, the evolution of the matrix damage $d_{\mathrm{M}}$ becomes higher, because more stress is transferred into the matrix, as less fiber interfaces are damaged. The overall macroscopic stress-strain relation therefore is stiffer for higher exponents. The higher ${\xi }_3$ the more the material behaves purely elastic.

Figure 3. Material response under uniaxial tension for varrying ${\xi }_3=k$, (a) Macroscopic stress-strain relation, (b) Evolution of load-carrying fiber fraction $c_{\mathrm{F}}$ and matrix damage $d_{\mathrm{M}}.$

Figure 3. Material response under uniaxial tension for varrying ${\xi }_3=k$, (a) Macroscopic stress-strain relation, (b) Evolution of load-carrying fiber fraction $c_{\mathrm{F}}$ and matrix damage $d_{\mathrm{M}}.$

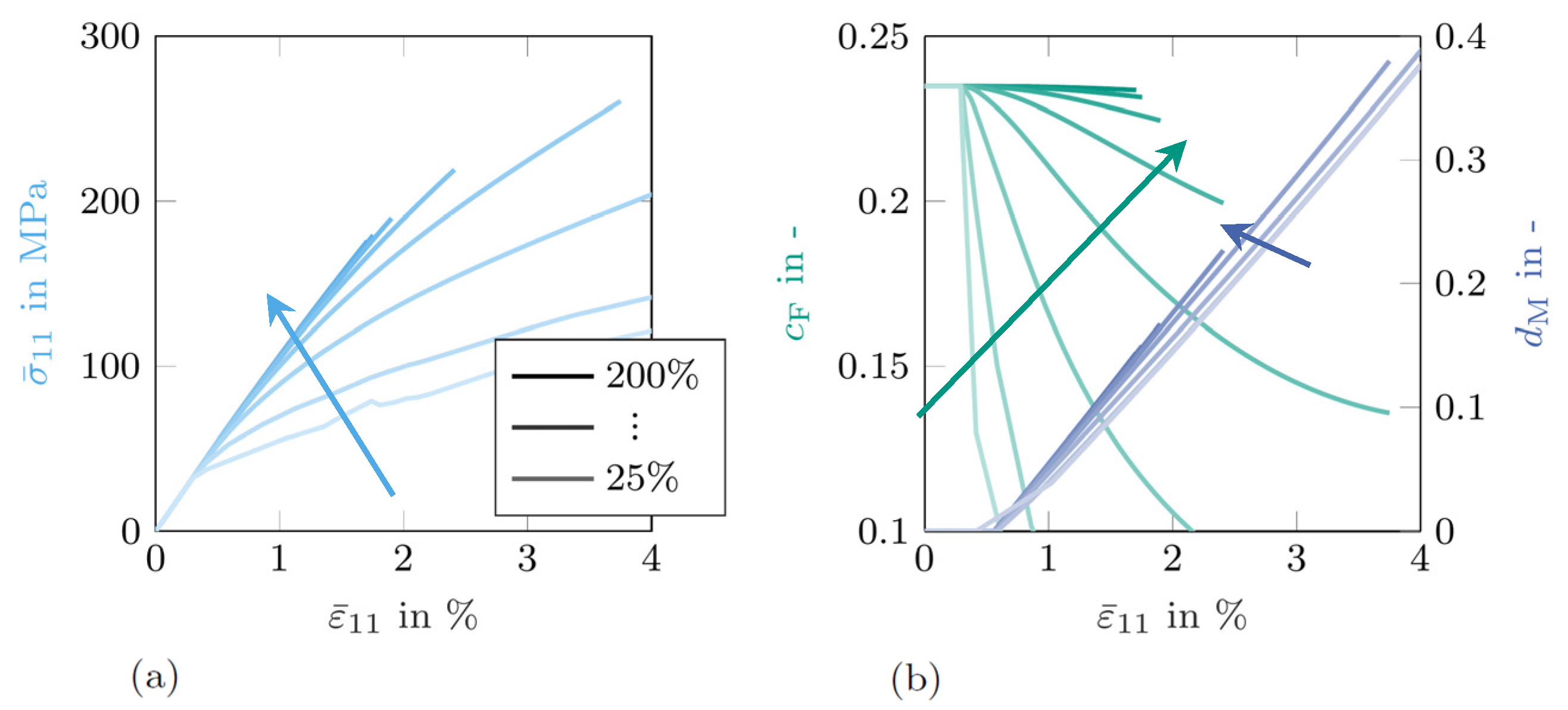
4. Conclusions

The presented, physically motivated and non-linear damage model by Schemmann et al. [1] is able to predict the evolution of load-carrying fibers and matrix damage on the microscale. The model yields reasonable results for the macroscopic stress-strain relation. The three independent parameters needed to describe the interface strength behave benevolent. The developed damage model can therefore be used to complete experimental characterizations. Within the International Research Training Group GRK 2078, e.g., uniaxial and biaxial tensile tests on continuous and discontinuous fiber reinforced SMC composites are performed (see Figure 4). Especially the damage behavior of discontinuous reinforced SMC composites under biaxial loading is not adequately understood so far. The presented model can help calibrate and understand such experiments, as well as acoustic emission analyses and vice versa. In combination with in-situ investigations a better understanding of the damage mechanisms can be achieved.

Furthermore, the model can be used to simulate structural components such as the reference structure shown in Figure 5. Parts are produced and tested under four-point bending. The development of the parts as well as the experimental investigations are accompanied by simulations based on the here presented model, in order to optimize the part and pre-calculate the critical areas. Those areas then are of major interest within the experimental setup.