Abstract
The time-averaged electronic speckle pattern interferometry (ESPI) is employed to measure the frequencies and mode shapes of thin, cantilevered plates with root-slit. The first 12 order linear resonance frequency and mode shape of an intact cantilevered plate is determined by using FEM calculation. The dynamic response of the intact specimen forced by a PZT actuator is measured and its super-harmonic resonance of forced response is investigated experimentally. The results show that the principal mode shape of super-harmonic vibration is similar to its natural modal. In contrast to linear forcing vibration, the threshold of force for super-harmonic resonance is much higher than that of the former. In addition, linear free response of four cantilevered root-slit plates with variation length of slit are analyzed by applying the FEM calculation, and their responses of forcing vibration were measured by using the ESPI method. The validity and accuracy of the numerical prediction are confirmed through experimental studies. The present work shows that the ESPI technique can provide whole-field and real-time measurement for vibration analysis and can also be employed for validation of the FEM calculation.
1. Introduction
It is well known that plate, shell, rod and beam are widely used in the construction of machines. Among them, thin plate is one of the most common structural elements in engineering design such as aviation and automobile. Its dynamic response is of importance to the design engineer and the study of the vibration behavior of a plate with a crack is a problem of great practical interest [1,2]. Numerous papers have been published on the vibration analysis of a finite cracked plate by using theoretical and numerical methods [3,4,5,6,7]. Nevertheless, compared with numerical studies in the past, there have been relatively few investigations on the behavior of the cracked plates by experimental measurement [8,9,10].
Before the advent of the finite element method, the vibration characteristics of plates with crack are studied by means of mathematical methods. In the literature [3], the deflection of the rectangular plate with crack is described by the Green’s function and then the first kind of homogeneous Fredholm integral equation is obtained. Stahl and Keer adopted the dual-series equations to study vibration and stability problems of the rectangular cracked plate, and finally converted into a solution of the second kind of homogeneous Fredholm integral equation [4]. For more complex structures, application of finite element methods comes naturally. In the research [5], by applying the Galerkin’s method and the incremental harmonic balance approach, the effects of various system parameters on the regions of instability and the non-linear response characteristics of rectangular cracked plates was investigated. In the work of Huang et al., the Ritz method was adopted to determine the frequencies and nodal patterns of thick, cracked rectangular plates analyzed using Mindlin plate theory. The effects of the length, location, and orientation of crack on frequencies and nodal patterns of cantilevered cracked rectangular plate have been investigated [6]. In the investigation of the linear and nonlinear vibration response of a cracked cantilevered rectangular plate, it was reported in literature [7] that a wider veering region entails continuous interchanging between the modes can be observed, and there exists fast mode switching in the smaller veering (or crossing) region. These phenomena obtained by the FEM prediction should be needed for validating furtherly by experimental measurement.
In this paper, the time-averaged ESPI technique and finite element method were used to study the linear and nonlinear vibration characteristics of an intact cantilevered plate and four cantilevered root-slit plates with different length of silt. This work was motivated by the whole-field and real-time mode shape observation of the ESPI method and the requirement for the vibration response validation of the FEM prediction. The first 12 order linear resonance frequency and mode shape of an intact cantilevered plate is determined by using FEM calculation. The ESPI method was then applied to measure the dynamic responses of the intact specimen under linear vibration and super-harmonic resonance. The measurement results for linear vibration well agree with those of the numerical simulation. The principal mode shape and threshold force of super-harmonic resonant response was obtained in the experimental investigation. The dynamic characteristics of four cantilevered root-slit plates are studied by FEM and ESPI methods, respectively. As analyzed by numerical method in the paper [7], the phenomena of the switching of mode shapes being owing to crack/slit length variation were verified experimentally in the end of this research.
2. Experimental Work and Mode Analysis
2.1. Specimens Preparation and Numerical Model
Five specimens used in this paper are aluminum rectangular plates of length 210 mm, width 80 mm and thickness 1.43 mm. As depicted in Figure 1, the specimens are clamped at one end and work as cantilever plates, the size of their free part is 165 × 80 × 1.43 mm3. Among these plates, one plate was in good condition (Figure 1a), the other four specimens as shown in Figure 1b–e have a side slit at the root with a length of 20 mm, 40 mm, 60 mm and 70 mm cut by electrical discharge machining, respectively.

Figure 1.
Photograph of five thin aluminum plates (a) Intact and (b–e) with different length slit cut by EDM.
The plates under test are excited by a small PZT actuator with diameter of 10 mm and thickness of 0.4 mm. The PZT actuator is attached the opposite face of the measured surface, the nodal lines should be avoided which can be predicted by FEM in advance. Thanks to the repetition of the PZT excitation, harmonic wave-field is formed in the tested plates and generate deflection displacement. Figure 2 illustrates the schematic diagram for deflection vibration measurement using the time-average electronic speckle pattern interferometry (ESPI) in this study. For the space limit, the measurement principle of ESPI method is not introduced in this paper, the readers can refer the literature [11] for detail. The sinusoidal vibration is measured during a frequency sweep using the optical setup illuminated in Figure 2. In the present study, a laser light with 80 mW and wavelength of 671 nm is used as a coherent light source. To achieve the sinusoidal output, a digitally controlled function generator (RIGOL DG1022Z) with maximum output frequency of 25 MHz connected to a power amplifier is employed.
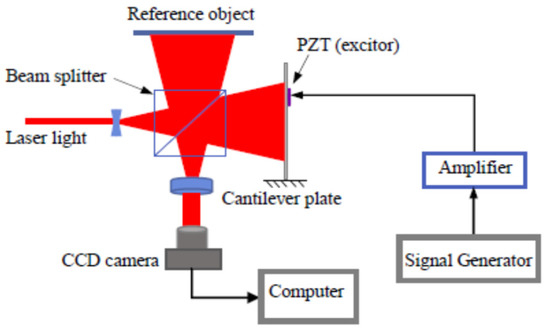
Figure 2.
The setup for out-of-plane vibration testing.
The finite element software ANSYS® is used for linear vibration analysis of aluminum rectangular plates with or without a slit. The physical and geometric parameters of the finite element model are Young’s modulus E = 70 GPa, Poisson’s ratio = 0.33, mass density = 2700 kg/m3 and size of 165 × 80 × 1.43 mm3, boundary condition is CFFF for the intact specimen. All the numerical results of resonant mode shapes are calculated by the commercial code ANSYS package in which SHELL 181 is selected. The shell is divided into a number of units with size of 1 mm × 1 mm × 1.43 mm.
2.2. Natural Frequencies and Mode Shapes
Table 1 shows the results of the experimental measurement and the finite element simulation of the first 12 and 15 order modes’ natural frequencies of cantilevered specimens 1–3 and 4–5, respectively. The natural frequencies obtained experimentally, shown in Table 1, is measured by frequency-sweeping. Figure 3a–l and Figure 3A–L, respectively, present the first 12 order mode patterns for intact cantilever plate from the finite element method simulation and ESPI experimental measurement. For the convenience of comparison, the results from FEM calculation were converted into fringe patterns. The brightest speckle fringes shown in Figure 3A–L denote nodal area where transverse displacement equals zero. Comparing with the FEM results presented in Figure 3a–l, it can be seen that the experimental results of the first 12 order modes are quite consistent with those of numerical prediction. Numerical and experimental results of natural frequencies of the first 12 modes are listed in column 2 in Table 1. All the experimental measured frequencies are almost equal to the numerical frequencies. Due to local stiffness enhance effect by the bonded PZT actuator, it can be seen, underlined digits as shown in Table 1, that some mode frequencies obtained by ESPI are greater than those of FEM prediction.

Table 1.
Natural frequencies (Hz) of the tested specimens from FEM and Experimental methods, respectively.

Figure 3.
Mode shapes of the first 12 resonant modes of CFFF aluminum plate from (a–l) FEM simulation and (A–L) experiment measurement, respectively.
2.3. Nonlinear Vibrating Response of the Intact Plate
In general, there is a range of external forces that can be applied, the most common of which for vibration problems is a continuous single-frequency sine wave force called harmonic forcing. As the input load amplitude increases and the material will yield and then exhibit a region of non-elastic behavior, the response of force-displacement becomes nonlinear. It is possible that the restoring force is not linear, and so for the single frequency harmonic input, the system response contains multiple components each with a different frequency. If the response harmonic frequency is three or five times as the input frequency, and so on, this phenomenon is so-called superharmonic resonance.
The forcing amplitude and corresponding response modes of the tested intact plate is experimental investigated. In order to determine the predominant response frequency, a high-speed camera was employed, and three series images of the intact specimen during its vibrating at frequencies of 124.45 Hz, 207.43 Hz and 622.4 Hz (622.4 Hz is its natural frequency of the first fourth mode) were recorded, respectively. All images were recorded at speed of 2000 fps. The intensity of one point was obtained from the series images (the number of selected images calculated is 1000 frames for each series.) by LUT and its FFT spectra is plotted as in Figure 4. As presented in Figure 4, when the forcing frequency is equal to 1/3, 1/5, even 1/7 of the natural frequency, the corresponding response modes measured by experiment are almost same as the natural mode shape. It can be found immediately that the principal response frequency is five times and three times than the input forcing frequency in Figure 4a and 4b, respectively. Due to the component presence of five times or three times of the input frequency, the tested specimen exhibits a superharmonic resonance.
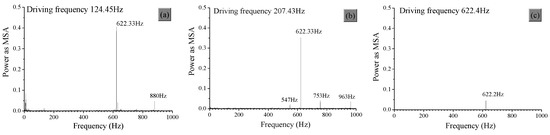
Figure 4.
FFT spectra of the intact specimen vibrating at different frequency.
2.4. Mode Shapes Vary with the Length of Root-Slit Variation
For the space limit, only the results of specimen 5 were presented in this paper. Figure 5 shows the first 14 mode shapes of specimen 5 obtained by FEM simulation and experimental measurement, respectively. The maps of resonant mode shapes from the finite element calculation are presented for comparison with the experimental observation. It can be seen that the results from experimental measurement keep excellent agreement with those of FEM prediction.

Figure 5.
Mode shapes of first 14 resonant modes of cantilevered aluminum plate with 7 cm root-silt: (a–n) FEM simulation and (A–N) Experiment measurement, respectively.
As expected, the resonant response of the plates with root-slit become sensitive to the slit length increasing. In order to closely see the mode shapes variation with the slit length increasing, two representative case are presented in Figure 6 and Figure 7. Figure 6 depicts mode 6, 7 and 8 variation as the slit length increasing, which shows that mode 6 changes its mode from shape (2, 1) to shape (3, 0) with the slit length variation, while its natural frequency is sensitive to slit length variation. Due to slit length variation, mode 7 varies modal shape (0, 2) into (2, 1), and mode 8 switches modal shape (4, 0) to shape (0, 2). For higher modes 10, 11 and 12, it can be observed from Figure 7 that response shapes are more affected by the length of slit and become complicated. [Note: the definition of mode shape (m, n) can be found in textbooks of Vibration Theory. Here, m stands for modal order of the bending, and n is for modal order of the torsional vibration.]
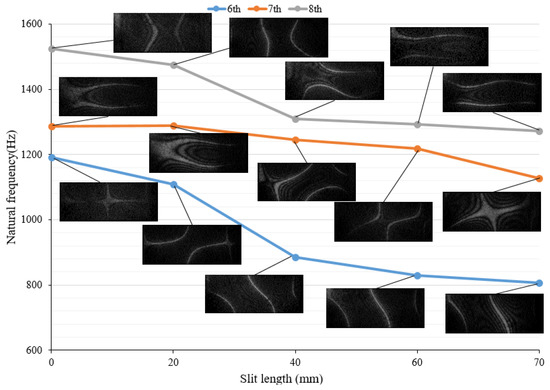
Figure 6.
Mode 6, 7 and 8 variation with the slit length increasing.
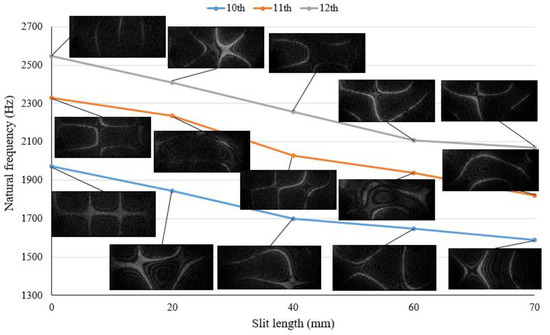
Figure 7.
Mode 10, 11 and 12 vary with the slit length variation.
3. Concluding Remarks
Using electronic speckle pattern interferometry (ESPI) method described in the present study, the vibration shapes of the tested plate surface can be full-field measured in real-time, and its natural frequencies can be obtained. Comparing with the calculation of the FEM method, it is indicated that the results from experimental measurement are excellent agreement with those of numerical prediction. It is also noted that the ESPI method can be used to provide measurement and analysis of nonlinear vibration. From the present experimental investigation, it was observed that, during superharmonic vibration of the cantilever plate, the principal mode shape is very similar to its natural mode, and the natural frequency is predominant in the response frequencies. The experimental work shows that superharmonic resonance only comes up after the driving force exceeds a threshold.
Furthermore, this research work has been demonstrated that the ESPI method can be employed to verify the FEM calculation. The results of the plates with root-slit obtained by experimental measurement were well validated with the results obtained by the numerical analysis. It should be pointed out that the ESPI method is suit for measuring deformation or displacement in the range of several ten micrometer.
Author Contributions
F.Y. and M.D. conceived and designed the experiments; N.T. performed the experiments; N.T. and Y.M. analyzed the data; H.J. contributed analysis tools; F.Y. wrote the paper. Investigation on non-linear vibration response of cantilevered thin plates with crack using Electronic speckle pattern interferometry.
Acknowledgments
The authors would like to acknowledge the support provided by National Natural Science Foundation of China (Nos. 11472081, 11772092, 11602056).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dimarogonas, A.D. Vibration of cracked structures: A state of the art review. Eng. Fract. Mech. 1996, 55, 831–857. [Google Scholar] [CrossRef]
- Qiu, Z.C.; Wu, H.X.; Ye, C.D. Acceleration sensors based modal identification and active vibration control of flexible smart cantilever plate. Aerosp. Sci. Technol. 2009, 13, 277–290. [Google Scholar] [CrossRef]
- Lynn, P.P.; Kumbasar, N. Free vibration of thin rectangular plates having narrow cracks with simply supported edges. Develop. Mech. 1967, 4, 911–928. [Google Scholar]
- Stahl, B.; Keer, L.M. Vibration and stability of cracked rectangular plates. Int. J. Solids Struct. 1972, 8, 69–91. [Google Scholar] [CrossRef]
- Wu, G.Y.; Shih, Y.S. Dynamic instability of rectangular plate with an edge crack. Comput. Struct. 2005, 84, 1–10. [Google Scholar] [CrossRef]
- Huang, C.S.; Leissa, A.W.; Li, R.S. Accurate vibration analysis of thick, cracked rectangular plates. J. Sound Vib. 2011, 330, 2079–2093. [Google Scholar] [CrossRef]
- Saito, A.; Castanier, M.P.; Pierre, C. Estimation and veering analysis of nonlinear resonant frequencies of cracked plates. J. Sound Vib. 2009, 326, 725–739. [Google Scholar] [CrossRef]
- Andreaus, U.; Baragatti, P. Experimental damage detection of cracked beams by using nonlinear characteristics of forced response. Mech. Syst. Signal Process. 2012, 31, 382–404. [Google Scholar] [CrossRef]
- Sundaresan, M.J.; Ghoshal, A.; Li, J.; Schulz, M.J.; Pai, P.F.; Chung, J.H. Experimental damage detection on a wing panel using vibration deflection shapes. Struct. Health Monit. 2003, 2, 243–256. [Google Scholar] [CrossRef]
- Maruyama, K.; Ichinomiya, O. Experimental study of free vibration of clamped rectangular plates with straight narrow slits. JSME Int. J. Ser. III 1989, 32, 187–193. [Google Scholar] [CrossRef]
- Wang, W.C.; Hwang, C.H.; Lin, S.Y. Vibration measurement by the time-averaged electronic speckle pattern interferometry methods. Appl. Opt. 1996, 35, 4502–4509. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).