Experimental Modal Analysis of Violins Made from Composites †
Abstract
:1. Introduction
2. The Prototype Violins
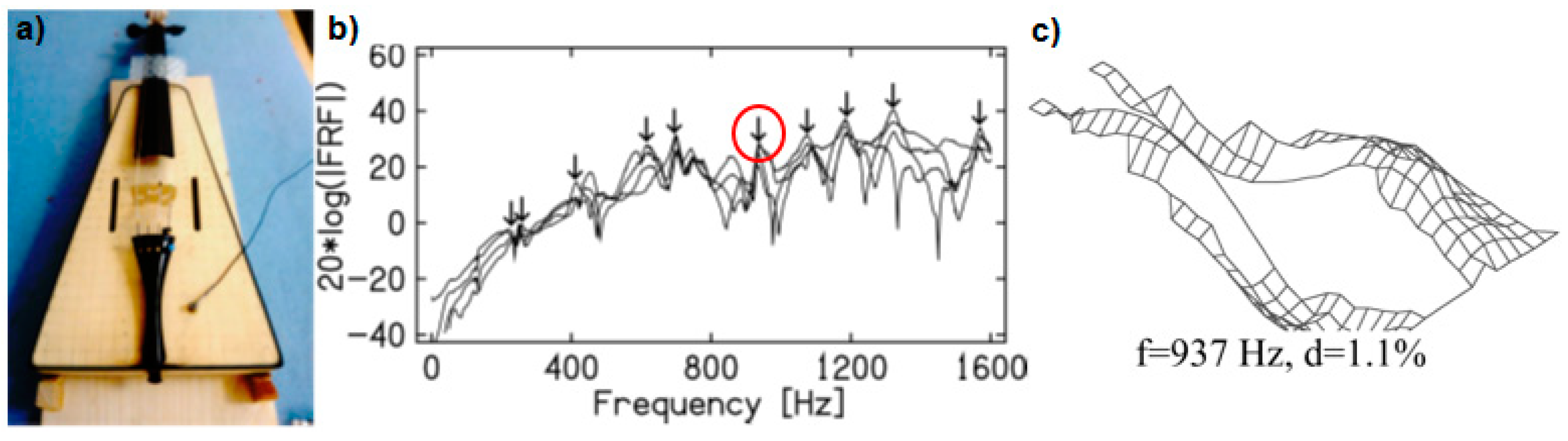
3. Modal Experiment
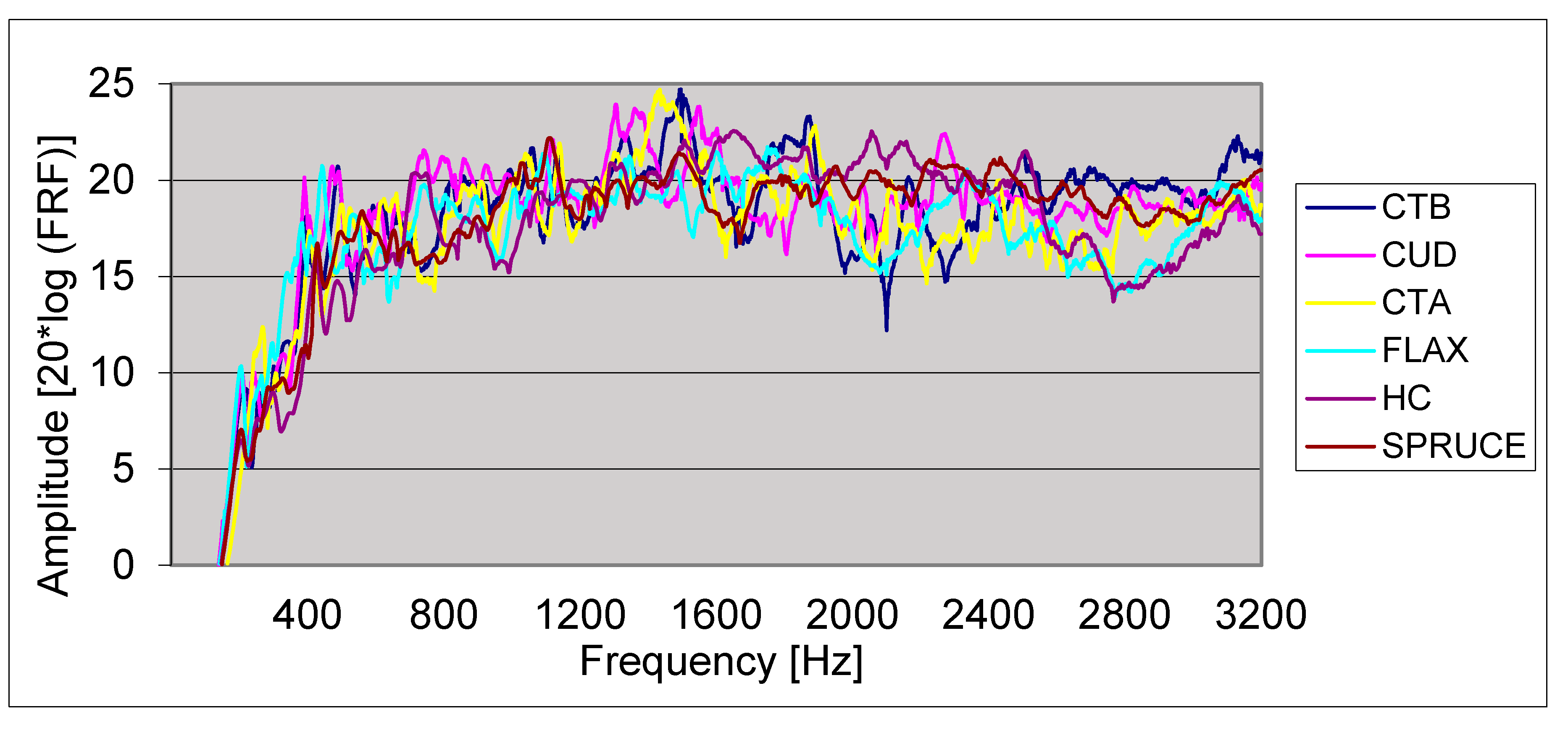
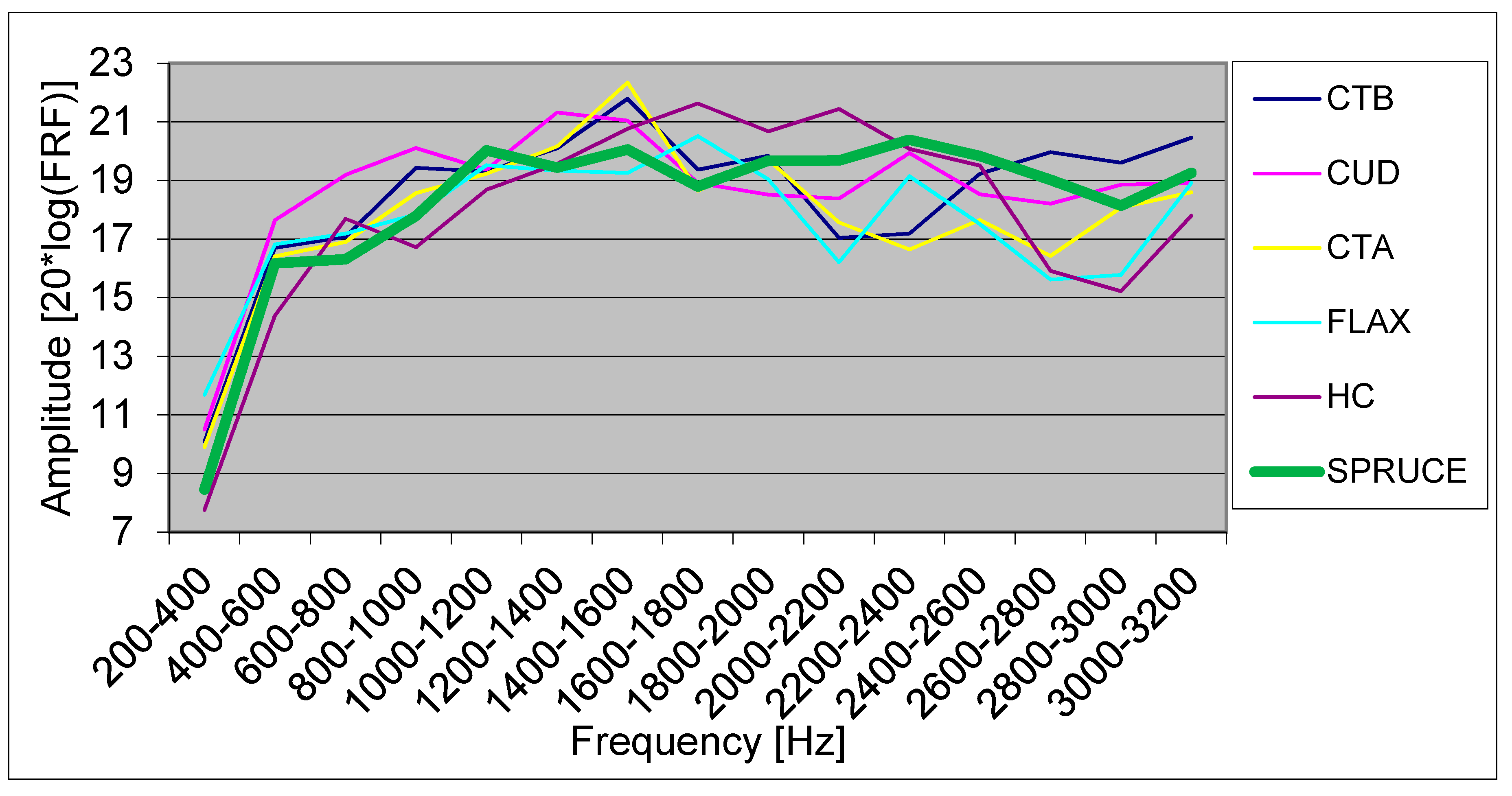
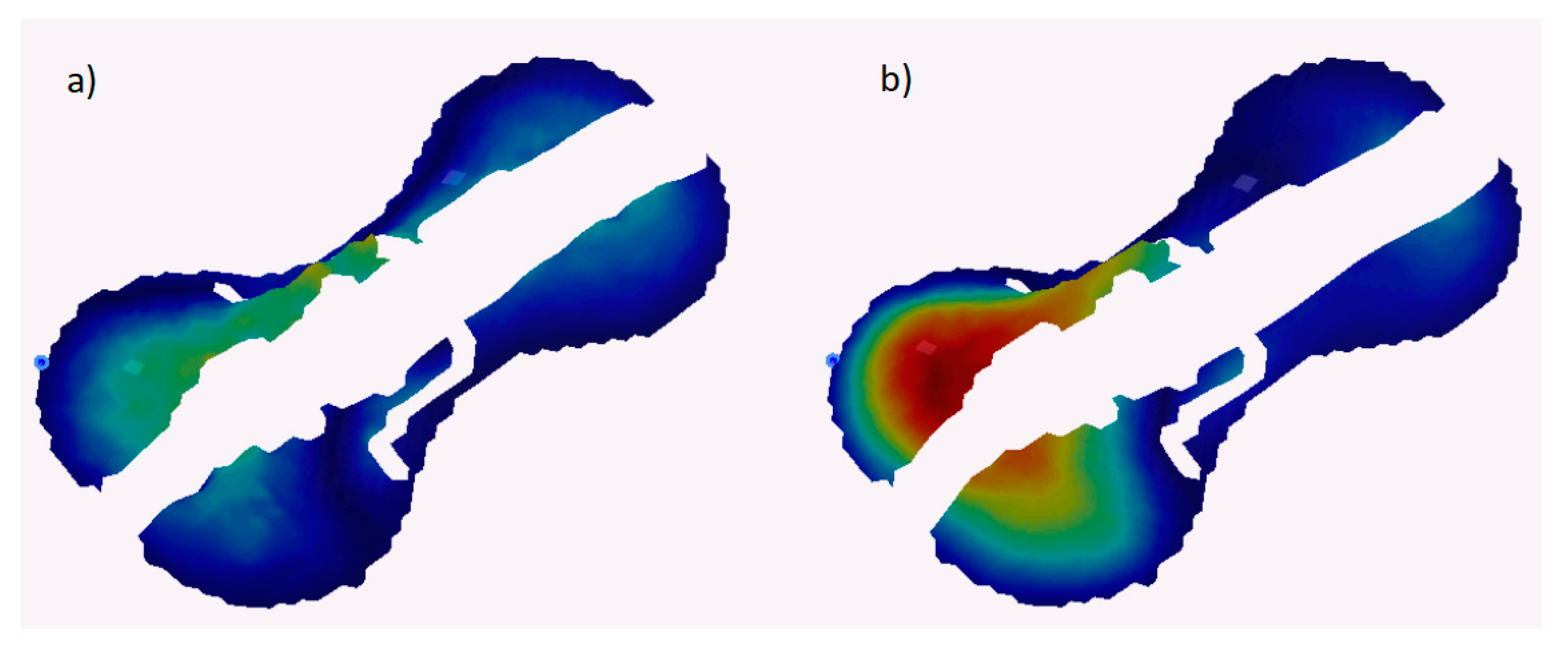
4. Results and Discussion
4.1. Other Measurement Methods for Modal Analysis of Violins
4.1.1. Excitation through Speaker
4.1.2. Excitation through Shaker
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Marshall, K.D. Modal analysis of a violin. J. Acoust. Soc. Am. 1985, 77, 695–709. [Google Scholar] [CrossRef]
- Torres, J.A.; Boullosa, R.R. Influence of the bridge on the vibration of the top plate of a classic guitar. Appl. Acoust. 2009, 70, 1371–1377. [Google Scholar] [CrossRef]
- Bissinger, G. Structural acoustics of good and bad violins. J. Acoust. Soc. Am. 2008, 124, 1764–1773. [Google Scholar] [CrossRef] [PubMed]
- Duerinck, T.; Skrodzka, E.; Linde, B.B.J. Modal analysis of a trapezoidal violin built after the description of F. Savart. Arch. Acoust. 2014, 39, 623–628. [Google Scholar] [CrossRef]
- Damodaran, A. An Overview of Fibre-Reinforced Composites for Musical Instrument Soundboards. Aust. Acoust. Soc. 2015, 43, 117–122. [Google Scholar] [CrossRef]
- Johnson, C.; Courtnall, R.; Menuhin, Y. The Art of Violin Making; Robert Hale: London, UK, 1999. [Google Scholar]
- Cough, C. Violin Acoustics. Acoust. Today 2016, 12, 22–30. [Google Scholar]
- Skrodzka, E.; Krupa, A.; Rosenfeld, E.; Linde, B.B.J. Mechanical and optical investigation of dynamic behavior of violins in modal frequencies. Appl. Opt. 2009, 48, 165–170. [Google Scholar] [CrossRef] [PubMed]
- Skrodzka, E.; Łapa, A.; Linde, B.B.J.; Rosenfeld, E. Modal parameters of two complete guitars differing in the bracing pattern of the soundboard. J. Acoust. Soc. Am. 2011, 130, 2186–2195. [Google Scholar] [CrossRef] [PubMed]
- Skrodzka, E.; Linde, B.B.J.; Krupa, A. Modal Parameters of Two Violins with Different Varnish Layers and Subjective Evaluation of Their Sound Quality. Arch. Acoust. 2013, 38, 75–81. [Google Scholar] [CrossRef]




| CTB | CUD | CTA | Flax | HC | Spruce | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Hz | % | Hz | % | Hz | % | Hz | % | Hz | % | Hz | % | |
| A0 | 221 | 200 | 251 | 198 | 192 | 199 | ||||||
| B1- | 393 | 2.10 | 391 | 2.64 | 409 | 2.43 | 380 | 3.38 | 423 | 2.36 | 424 | 2.57 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duerinck, T.; Kersemans, M.; Skrodzka, E.; Leman, M.; Verberkmoes, G.; Paepegem, W.V. Experimental Modal Analysis of Violins Made from Composites. Proceedings 2018, 2, 535. https://doi.org/10.3390/ICEM18-05457
Duerinck T, Kersemans M, Skrodzka E, Leman M, Verberkmoes G, Paepegem WV. Experimental Modal Analysis of Violins Made from Composites. Proceedings. 2018; 2(8):535. https://doi.org/10.3390/ICEM18-05457
Chicago/Turabian StyleDuerinck, Tim, Mathias Kersemans, Ewa Skrodzka, Marc Leman, Geerten Verberkmoes, and Wim Van Paepegem. 2018. "Experimental Modal Analysis of Violins Made from Composites" Proceedings 2, no. 8: 535. https://doi.org/10.3390/ICEM18-05457
APA StyleDuerinck, T., Kersemans, M., Skrodzka, E., Leman, M., Verberkmoes, G., & Paepegem, W. V. (2018). Experimental Modal Analysis of Violins Made from Composites. Proceedings, 2(8), 535. https://doi.org/10.3390/ICEM18-05457





