Analysis of Inclined Cracks in Thin-Walled Circular Tube under Mixed-Mode I + II Fracture ^†

Abstract

This paper provides a study on mixed-mode fracture mechanics in thin-walled tube which is subjected to tension, shear and torsion loading. This type of loading causes an inclined crack to develop and generate a mixture of normal and shear stresses ahead of a crack tip. The stress state ahead of a crack tip is frequently based on mixed-mode type of interactions which designate the amplitude of the crack tip stresses. The analytical expressions for the stress intensity factors for mixed-mode I + II approach are presented. The Paris law for mixed-modes I + II has been discussed. Mixed-mode fracture mechanics is used with theoretical models to predict the path of crack growth when an inclined crack is subjected to a combination of mode I and mode II deformations. The torque at which crack propagation can be expected has been determined. The numerical calculations have been carried out by using MATLAB code. The results are good and could be useful for companies working with thin-walled circular tubes.

1. Introduction

Production and use of steel structures were found to be accompanied by failures and breakdowns of structures such as rails, vessels, large tanks, boilers, bridges and many more. Defects in structures may be the main cause of failures and breakdowns. Some problems in thin-walled circular tubes occur due to sudden brittle fractures in welded structures.

The stress field at the tip of the cracks should be studied in order to ensure safety of structures. A fracture in real metals is carried out by a process of deformation and local failure at the front of a slowly or rapidly propagating crack. Cracks in brittle structures are often governed by linear elastic fracture mechanics. Most of the previous studies on structures are focused on the mechanisms of crack initiation and propagation of Mode I cracks [1,2,3,4,5].

The most common understanding of Mode II failure is that shear mode crack growth is caused by a linkage of many small tensile cracks [6,7]. It is believed that at a mixed-mode I + II fracture, the crack grows in a direction that maximizes one of the stress intensity factors $K_I$ or $K_{II}$, rather than in a direction that maximizes both stress intensity factors $K_I$ and $K_{II}$ simultaneously.

The stress intensity factor is mostly used as a parameter to evaluate the state of stress near the crack tip according to Linear Elastic Fracture Mechanics (LEFM) approach. The inclined propagating cracks are analyzed for the direction of propagation of cracks. Numerical methods have many advantages to solving the fracture problems [8,9,10,11] and this is the approach of this study.

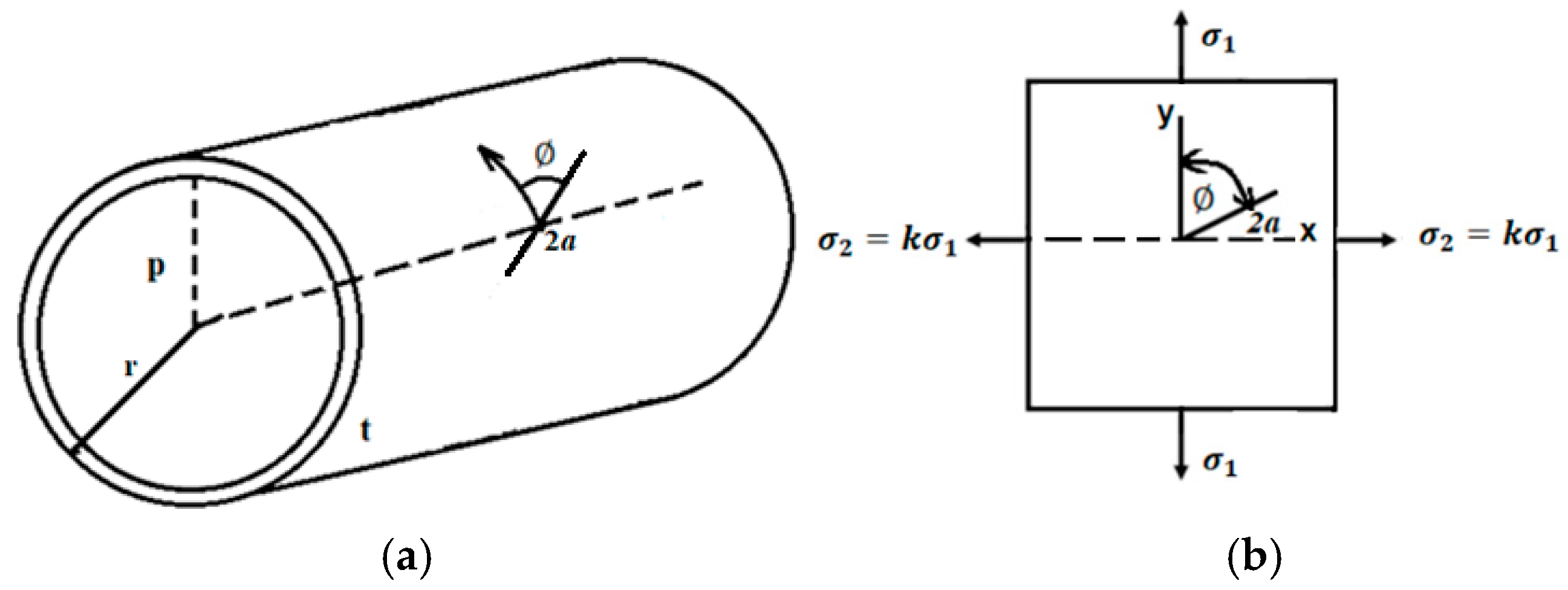
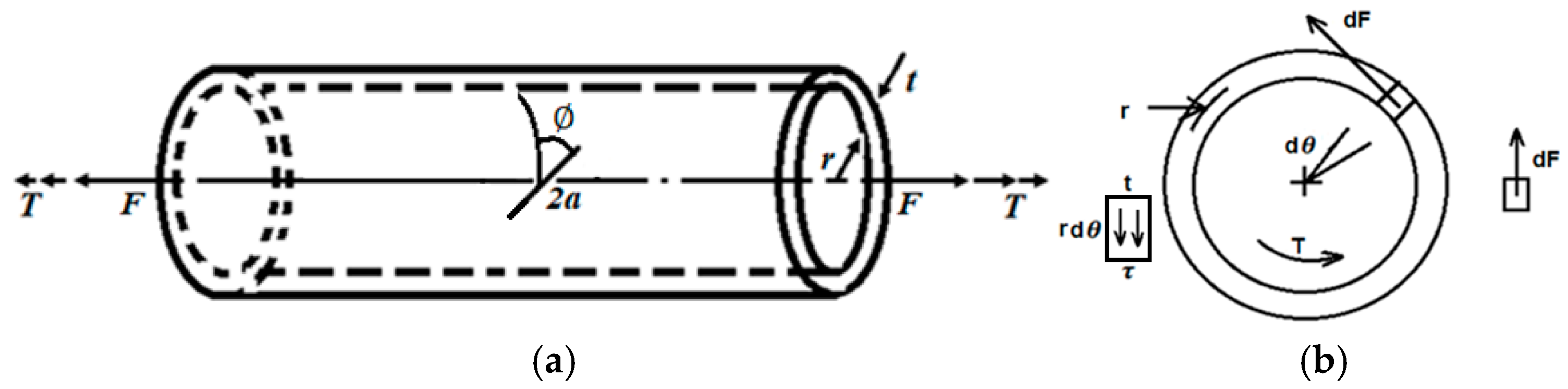
2. Mathematical Modeling for the Mixed-Mode I + II

In this study, a central inclined crack of length 2a in a thin-walled circular tube as shown in Figure 1a, is considered. When the tube is loaded biaxially, flaws will be subjected to mixed loading as shown in Figure 1b. The stresses are ${\sigma }_1$ and ${\sigma }_2=k{\sigma }_1$ along the y and x directions, respectively. Mode I will result in opening of the crack faces while Mode II will cause a sliding motion of the crack faces along the length of the crack.

The stress intensity factors $K_I$ and$K_{II}$ for the tensile and shear mode [12] are derived using Equations (1) and (2) as

$$K_I=K_{I1}+K_{I2}=\left(si{n}^2\varnothing +kco{s}^2\varnothing \right) {\sigma }_h\sqrt{\pi a},$$

(1)

$$K_{II}=K_{II1}+K_{II2}=\left(1-k\right)sin\varnothing cos\varnothing {\sigma }_h\sqrt{\pi a}$$

(2)

$$K_{III}=0$$

(3)

where ${\sigma }_h$ is the hoop stress on the tube and the tensile stress and the shear stress acting on the crack are given in the form

$${\sigma }_I={\sigma }_{I1}+{\sigma }_{I2}=\left(si{n}^2\varnothing +kco{s}^2\varnothing \right){\sigma }_h \mathrm{and} {\tau }_{II}={\tau }_{II1}+{\tau }_{II2}={\sigma }_h\left(1-k\right)sin \varnothing cos\varnothing$$

The longitudinal and hoop stresses in the circular tube are obtained from the equilibrium and are given as

$${\sigma }_a=\frac{pr}{2t}$$

(4)

$${\sigma }_h={\sigma }_I=\frac{pr}{t}$$

(5)

respectively. Equations (4) and (5) can be used to find$k=\frac{1}{2}$. The stress intensity factors for Mode I and Mode II in Equations (1) and (2) become [13]

$$K_I=\left(si{n}^2\varnothing +kco{s}^2\varnothing \right)\frac{pr}{t}\sqrt{\pi a}$$

(6)

$$K_{II}=\left(1-k\right)cos\varnothing sin\varnothing \frac{pr}{t}\sqrt{\pi a}$$

(7)

The tube is now loaded by a torque T and an axial tensile force F. In this case, it is assumed that r >> t so that the curvature of the tube may be neglected when the stress intensity factor is determined. The normal stress is given by the axial tensile force, F in the longitudinal direction and the shear stress is given by the torque T, as shown in Figure 2a.

In Figure 2b, a thin-walled circular tube is subjected to a twisting moment T. The mean radius is given by $r_m$, a typical small area of length $rd\theta$and thickness t transmitting an increment of force $dF=\tau \left(trd\theta \right)$ are assumed [14]. The moment of the incremental force about the axis of the circular tube equals the applied torque T. Therefore [14]

$$T={{\displaystyle \oint }}^{}rdF=\underset{0}{\overset{2\pi }{{\displaystyle \oint }}}r\tau trd\theta =2\pi \tau t{r}^2$$

(8)

$$\tau ={\tau }_{xy}=\frac{T}{2\pi r^{2}t}$$

(9)

The two-dimensional Cartesian stress transformation equations [15,16] are given as

$${\sigma }_{x^{\prime }}={\sigma }_{x}co{s}^2\varnothing +{\sigma }_{y}si{n}^2\varnothing +2{\tau }_{xy}sin\varnothing cos\varnothing$$

(10)

$${\sigma }_{y^{\prime }}={\sigma }_{x}si{n}^2\varnothing +{\sigma }_{y}co{s}^2\varnothing -2{\tau }_{xy}sin\varnothing cos\varnothing$$

(11)

$${\tau }_{x^{\prime }{y}^{\prime }}=\left({\sigma }_y-{\sigma }_x\right)sin\varnothing cos\varnothing +{\tau }_{xy}\left(co{s}^2\varnothing -si{n}^2\varnothing \right)$$

(12)

For the purpose of this study, the stress ${\sigma }_{x^{\prime }}$ gives a normal stress ${\sigma }_{n\varnothing }$ across the crack which then loads the crack in Mode I. The shear stress ${\tau }_{x^{\prime }{y}^{\prime }}$ gives a normal shear stress across the crack ${\tau }_{n\varnothing }$ which then loads the crack in Mode II, where ${\sigma }_{x^{\prime }}={\sigma }_{n\varnothing }$ and ${\tau }_{x^{\prime }{y}^{\prime }}={\tau }_{n\varnothing }$. Thus, the stress intensity factors $K_I$and $K_{II}$ for a small inclined crack can be expressed in the form [17]

$$K_I={\sigma }_n{f}_1\sqrt{\pi a}={\sigma }_{n\varnothing }\sqrt{\pi a}=\frac{\sqrt{3}}{2}{\tau }_{xy}\sqrt{\pi a}$$

$$K_{II}={\sigma }_n g_1 \sqrt{\pi a}={\tau }_{n\varnothing }\sqrt{\pi a}=\frac{1}{2}{\tau }_{xy}\sqrt{\pi a}$$

where $f_1$ and $g_1$ are factors that are equal to 1 and ${\sigma }_{n\varnothing }=\frac{\sqrt{3}}{2}{\tau }_{xy}\sqrt{\pi a}$ and ${\tau }_{n\varnothing }=\frac{1}{2}{\tau }_{xy}\sqrt{\pi a}$ by using $\varnothing ={30}^0$, ${\sigma }_x=0$ and ${\sigma }_y=0$.

The maximum circumferential stress criterion [18], is based on the assumption that the crack will grow in the direction such that the Model I stress intensity factor is maximized. During a biaxial loading cycle, it is crucial to determine the fatigue crack growth direction. Applying the maximum tangential stress criterion, the crack extension direction can be given b [18]

$$\theta =2ta{n}^{-1}\left\{\frac{1}{4}\left[\frac{K_I}{4K_{II}}\pm \frac{1}{4}\sqrt{{\left(\frac{K_I}{4K_{II}}\right)}^2+8}\right]\right\}$$

(13)

where $\theta$ is the crack propagation direction. The equivalent stress intensity factors can be given in the form [17,19,20]

$$K_{eq\left(A\right)}={\left(K_I^2+{\alpha }_I{K}_{II}^2+\frac{4}{k+1}{K}_{III}^2\right)}^{0.5}$$

(14)

$$K_{eq\left(B\right)}={\left(K_I^2+{\alpha }_I{K}_{II}^2\right)}^{0.5}$$

(15)

$$K_{eq\left(C\right)}={\left(K_I+{\alpha }_I{K}_{II}\right)}^{0.25}$$

(16)

where ${\alpha }_I=1, 2, 8$ for Equations (14)–(16) respectively and $\Delta K_{III}=0$ for the thin-walled tube. Fracture is expected when $K_{eq}=K_{Ic}$ if LEFM can be used, therefore the value of the torque can be found as

$$T=\frac{K_{Ic}2\pi r^{2}t}{\sqrt{\pi a_c}}$$

(17)

$$a_c=\frac{1}{\pi }{\left(\frac{K_{Ic}t}{pr}\right)}^2$$

(18)

where $a_c$ is the critical crack length. Fracture toughness is a measure of the ability of a material to resist the growth of a pre-existing crack or flaw, that is, it is a critical value of the stress intensity factor $K_I$ at the time of an unstable crack propagation, that is, $K_I=K_{Ic}$.

3. Law of Fatigue Crack Propagation

In the 1960’s, Paris [21] postulated that the range of stress intensity factor might characterize sub-critical crack growth under fatigue loading in the same way that $\Delta K$ characterized fast fracture. To analyze the mixed-mode fatigue crack, the Paris law [21] should be redefined by replacing $\Delta K$ with an equivalent stress intensity factor which takes into account both modes of fracture. Thus,

$$\frac{da}{dN}=C{\left(\Delta K_{eq}\right)}^m=C{\left[\Delta K_I^2+\Delta K_{II}^2\right]}^{\frac{m}{2}}$$

(19)

where Equations (14)–(16) are used, C is the Paris coefficient and m is the slope stress ratio. The equivalent stress intensity factors in Equations (14)–(16) are selected for the calculation of the fatigue crack growth rate considering relative variation of the $K_I$ and $K_{II}$.

4. Numerical Experimental Procedures

For this study, the crack propagation is the main parameter for the fatigue damage. A thin-walled circular tube is made from Ti alloy (Ti-6Al-4V Grade 5) [22] with $K_{Ic}$ of $107 \mathrm{MPa}\sqrt{m}$, yield strength ${\sigma }_{ys}$ of 1200 MPa, elastic modulus E = 119 GPa, the coefficient of Paris law of C = $6.0\times {10}^{-10}$ the internal pressure p = 250 MPa producing a circumferential hoop stress ${\sigma }_h$ of 360 MPa and the Poisson’s ratio $v=0.37$. The tube has surface flaw oriented at angle $\varnothing ={60}^0$ to the uniform tensile hoop stress. The tube was regularly subjected to Nondestructive Testing inspection. The inspection showed that the tube contained an angled flaw of length 2a (a = 1.0 mm). The inner radius is 45 mm and the outside radius is 50 mm, while the wall-thickness of the tube is $t=r_2-r_1$, and length l = 5 m.

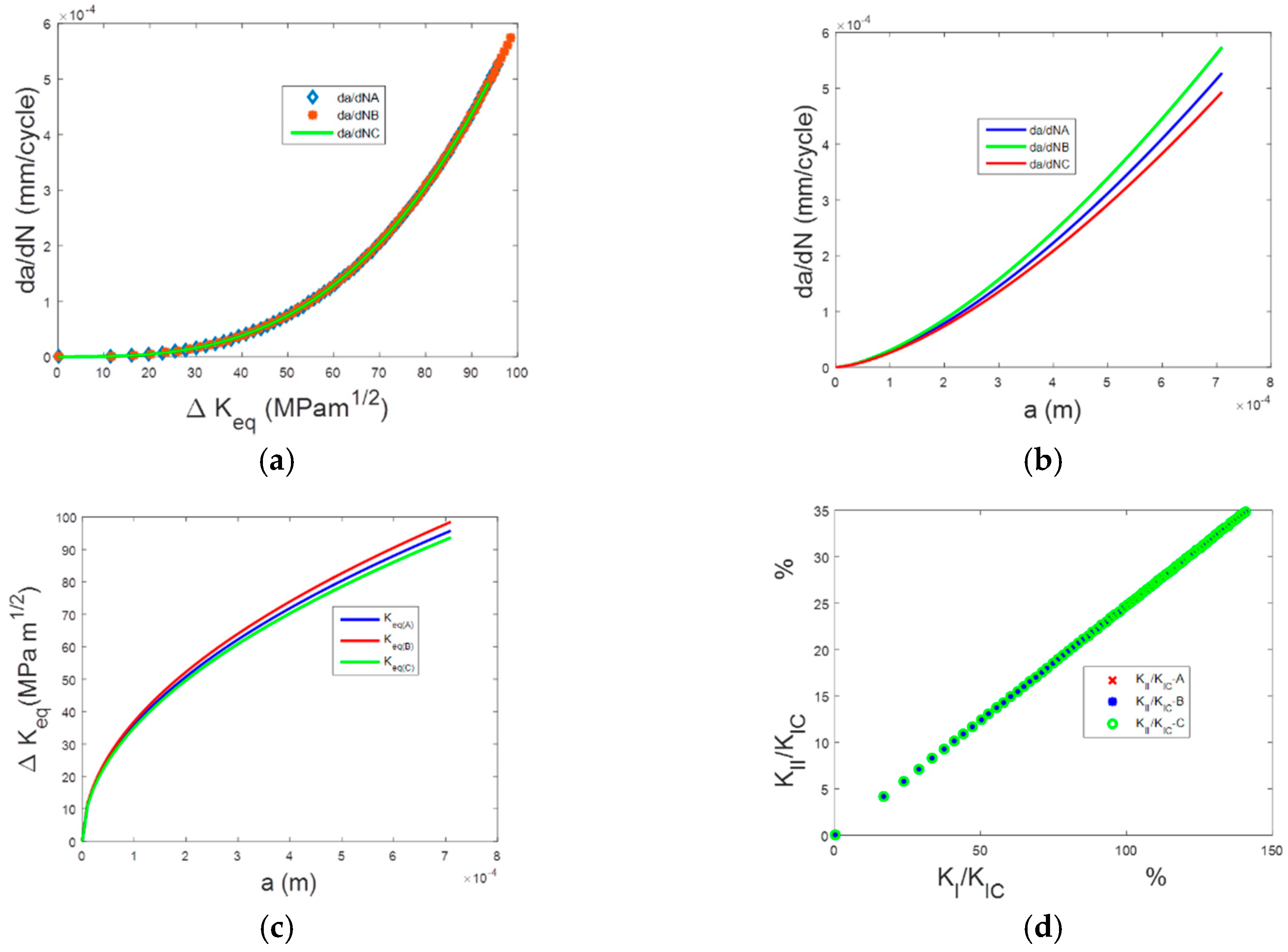
5. Calculations and Results

The results were obtained using the Matlab script. Figure 3a shows the $K_I$ and $K_{II}$ values that have been estimated theoretically and it can be noticed that $K_I$ values are predominant over $K_{II }$ values.

Therefore the crack is influenced more by stress intensity factor in Mode I. The torque from Equation (17) has been calculated and the value is 145.2 kNm at $a_c=7 \mathrm{mm}$. The predominant Mode loading caused a crack path deviation by ${0.83}^0$when Equation (13) was used. The critical crack length was obtained to be $7.1987\times {10}^{-4}$ m using Equation (18). Figure 4a provides theoretically analyzed values of da/dN versus the $\Delta K_{eq}$ values, while Figure 4b shows theoretically analyzed values of da/dN versus the crack length. It can be noticed that the curves of Figure 4a do not vary significantly while those of Figure 4b vary slightly significantly.

In Figure 4c the equivalent stresses of Equations (14) and (15) are plotted against the crack length and it can be seen that there is a slight significance between them. In Figure 4d, it can be confirmed that the $K_{eq}\left(B\right)$ is predominant over both $K_{eq}\left(A\right)$ and $K_{eq}\left(C\right)$, while $K_{eq}\left(A\right)$ is predominant over $K_{eq}\left(C\right)$. All $\frac{K_{II}}{K_{Ic}}$ for A, B and C behave the same way as seen in Figure 4d. It is interesting that in Figure 4c, da/dN B dominates both da/dN A and da/dN C respectively.

6. Conclusions

Analysis of an inclined crack on thin-walled circular tube under mixed-mode I + II fracture has been studied in the present work. The crack propagation is the main parameter for the fatigue damage. The flaw is inclined at an angle to the direction of the hoop stress. So the hoop and longitudinal stresses are the most critical stresses. The numerical calculation of K for Mode I and Mode II were carried out. The results were obtained using the Matlab script.

It can be noticed that the values obtained for $K_I$ are predominant over those obtained for the$K_{II}$. The major results of this study are summarized in the plots. The torque at which a crack propagation can be expected has been found and looks reasonable for this study. The angle for the crack extension direction has been determined. The results obtained in this study are good and could be useful for companies working with thin-walled circular tubes.