Abstract
Metals with a fine-grained microstructure have exceptional mechanical properties. Severe plastic deformation (SPD) is one of the most successful ways to fabricate ultrafine-grained (UFG) and nanostructured (NC) materials. Most of the SPD techniques employ very low processing speeds. However, the lowest steady-state grain size which can be obtained by SPD is considered to be inversely proportional with the strain rate at which the severe deformation is imposed. In order to overcome this limitation, methods operating at higher rates have been envisaged and used to study the fragmentation process and the properties of the obtained materials. However, almost none of these methods, employ hydrostatic pressures which are needed to prevent the material from failing at high deformation strains. As such, their applicability is limited to materials with a high intrinsic ductility. Additionally, in some methods the microstructural changes are limited to the surface layers of the material. To circumvent these restrictions, a novel facility has been designed and developed which deforms the material at high strain rate under high hydrostatic pressures. Using the facility, commercially pure aluminum was processed and analysis of the deformed material was performed. The microstructure evolution in this material was compared with that observed in static high pressure torsion (HPT) processed material.
1. Introduction
Fine-grained metals have been investigated extensively over the last decade which has culminated into development of many SPD techniques. A few of them were even explored to be scaled up from laboratory prototypes [1,2]. However, during SPD, after reaching a stable region, further fragmentation of microstructure and as a result refinement of grain size cease, even if straining is continued to very large strain values. This is due to the occurrence of a steady-state regime which is considered to be largely a function of the specific deformation technique at a given temperature and strain rate [3]. In order to enhance the limit of grain fragmentation, several studies have been conducted either at lower deformation temperatures or at higher strain rates. Metals deforming via slip exhibit similar deformation structures when processed at higher strain rates or at lower temperatures or when the material stacking fault energy (SFE) is low. The deformation imparted at high strain rates is known to produce a decreased cell size and increased misorientation owing to more dislocations trapped inside the individual cells. Moreover, under high strain rates suppression of the thermally activated dislocation processes can lead to high flow stresses, enough to activate twinning even in high stacking fault energy materials [4]. Thus providing additional deformation mechanisms and further fragmentation of the structure.
Most of the high strain rate, severe deformation studies published so far rely on uniaxial compression facilities where the deforming material is unconfined and is allowed to flow freely [5,6]. Such facilities can be of two types: (i) conventional upper-lower anvil type presses [5] or (ii) the split Hopkinson pressure bar system and their adaptations [6]. In addition few studies report the use of torsional deformation devices which can be either torsional Kolsky bar systems [7] or conventional torsion deformation devices [8]. However, all of the above methods of dynamic deformation suffer from their inability to apply hydrostatic pressure on the material during SPD, which seriously limits the amount of strain that can be imparted, without the failure of material. This also means that the use of these methods for SPD is restricted for materials with high intrinsic ductility. Ball milling [9], machining [10] and surface mechanical attrition methods [11] have also been explored in order to study the effects of a high strain rate deformation on the microstructure and properties of metals. The major drawback of these methods is that the microstructural changes occur only in the surface layers of the material and the cross-section of processed material is insufficient for further mechanical property characterization. Additionally, they only provide an opportunity to understand the evolution of the materials microstructure with strain rate, and are unusable as SPD metal forming operation in which a certain amount of material is deformed and fragmented into fine-structured material.
In present work, a novel high strain rate deformation facility is introduced, where similar to HPT processing a thin disk- or ring-shaped specimen is deformed in simple shear conditions under an applied axial load. Purpose-developed molds holding the sample and an axial load constricts the material flow during deformation and produce a hydrostatic pressure. Named dynamic high pressure torsion (DHPT), the setup has been used to process commercially pure aluminum. The obtained microstructures and properties after deformation are presented along with those of annealed and statically deformed material.
2. Experimental Method
2.1. High Pressure Torsion (HPT)
HPT has been one of the most successful methods for SPD and has been employed to process a variety of materials, such as Al, Cu, Al-Cu system, Fe, Ti-Fe alloy system, Nd-Fe-B alloys system, etc. This is because HPT is capable of introducing very large shear strains in the material in a single cycle of operation as opposed to other SPD methods, Equal channel angular pressing (ECAP) or Accumulative roll bonding (ARB), where multiple passes are required to accumulate the SPD strain.
HPT process consists of applying shear deformation to a sample held between two molds, under very high hydrostatic pressure. Three distinct configurations of HPT have been reported in literature. In the simplest unconstrained configuration, the material is free to flow outwards in radial direction and very little back pressure exists on the material due to the frictional forces acting between the sample and mold. On the other hand in constrained HPT, the sample perfectly fits into the cavity in one of the molds and the material is not allowed to flow in outward direction during torsional deformation. However, the quasi-constrained configuration is the most commonly used. Here the sample thickness is slightly larger than the height of the cavity available in both upper and lower mold combined. After the application of axial load, material flows between the two molds, restricting further outflow and thus building the back-pressure essential for torsional straining thereafter. In present investigation, the HPT and DHPT, use the quasi-constrained configurations.
In HPT, the equivalent strain exerted onto the material is calculated using following equation:
where γ is the shear strain applied, N is the number of revolutions, and r and h are the radius and thickness of the sample, respectively. From above equation it can be seen that with increasing radius the applied shear strain increases and thus gives an opportunity to see the evolution of the microstructure with accumulating torsional strain when moving from inside to the outside in radial direction.
Though HPT is capable of applying infinitely large shear strains to the material, the microstructure is prone to a saturation effect where no further fragmentation is observed in the material. Hence in order to further augment the refining capability of HPT, a novel dynamic HPT facility was devised and is explained in the next section.
2.2. Dynamic High Pressure Torsion (DHPT)
In DHPT, as already stated above, the material deformation conditions are exactly the same as those in HPT. In addition, the DHPT facility is based on the principle of split Hopkinson torsion bar (SHTB) systems in order to produce high strain rate torsional deformation. The SHTB system was devised and first reported by Baker and Yew, to characterize the high strain rate response of commercially pure copper to torsional loading [12]. In the original design, the torsional elastic wave was applied to the sample, a cylindrical tube, and silver brazed between the two steel tubes, called input or loading rod and output rod. The input loading rod is pre-twisted at one end and clamped at the other end near the specimen. A sudden release of the clamp allows propagation of a torsional elastic wave towards the unstressed bar and finally to the specimen, deforming it at a very high strain rate.
The governing equation for the motion of a torsional elastic wave in a cylindrical bar is given by [13]:
where θ(x, t) is the rotation angle at time t of a section at location x along the bar, is the wave velocity, and are the shear modulus and density of the loading bar, respectively. The amplitude of the strain pulse is controlled by the amount of twist applied to the loading rod and further in an elastically loaded bar the pre-torque, is related to the shear strain measured at the bar surface, by the following equation:
where is the radius of the bar and is the polar moment of inertia which for a solid cylindrical bar is equal to .
The amplitude of the incident wave is half the amplitude of the pre-torque, i.e., the incident torque, is equal to . Using the value of , the rotational speed, acting on the bar after the release of torsional energy can be calculated as given below:
where , is the torsional impedance of the bar. Following the interaction, at the specimen, a part of the torsion strain pulse is reflected while another component is transmitted to the output rod through the specimen. Thus the resultant rotational speed at the sample is then given by:
where and are the rotational speeds at the input bar/sample interface and sample/output bar interface, respectively; and are the reflected and transmitted torque, and and are the torsional impedances of the input and output bars, respectively.
However, unlike the SHTB system, in DHPT the purpose was: (i) to maximize the strain amplitude in a given cycle, (ii) prevent the failure of the sample material during shear deformation, and (iii) avoid the transfer of a part of the rotational energy to the output rod, ultimately to increase the shear deformation on the sample. To achieve this, significant conceptual alterations were made while designing the DHPT system. The schematic of the DHPT facility is shown in Figure 1.
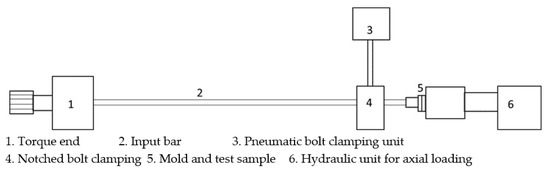
Figure 1.
Schematic presentation of the DHPT setup (not to the scale).
To prevent the partial loss of transmitted rotational energy, instead of the output rod a fixed clamp which holds the other part of the sample mold, was used. This fixed clamp, like the loading bar has a hexagonal cavity at its end, to hold a part of the mold containing a ring sample to be deformed. At one end (at the right side in Figure 1), the fixed clamp is connected to the hydraulic system which applies the axial load onto the whole system, i.e., the sample and loading bar, so as to produce the necessary hydrostatic pressure condition. Hence the second term on the right side of Equation (6) becomes zero, and thus the rotational speed at sample in DHPT is given by:
Thereby inserting Equation (7) in Equation (1) gives the effective shear strain rate in the sample. It is interesting to note here that the strain rate varies linearly with the radius of the sample and the maximum strain rate can be observed at the outer boundary of the sample.
In DHPT, a solid input bar is used. This solid loading bar was twisted using a pneumatic system (on the left side in Figure 1). Additionally, because of very low density of Al alloys when compared to steel, Al-7075 alloy in T6 tempered condition was used as bar material. In order to increase the duration of the strain pulse and as a result the shear deformation, almost the entire length of the input bar was pre-torqued, by putting the mechanical clamp very close to the sample position.
The rise time of the strain pulse is decided by the time required for releasing the clamp. In order to achieve a sudden release of the torque, two techniques have been used in SHTB systems, viz. the fracture of a brittle disc or rod, and the release of the friction clamp. In present facility the friction clamping mechanism is used. Here a notched bolt is used to clamp onto the loading bar and the same is broken at the start of the test, using a pneumatic cylinder system, to release the stored torsional energy.
In DHPT, the failure of the deformed material is prevented by providing semi constrained deformation conditions to the sample material, as explained in Section 2.1. Figure 2a shows the part of the mold to be inserted on the loading bar side. In present investigation, a ring shaped sample is used and hence the annular gap at the center of the mold.
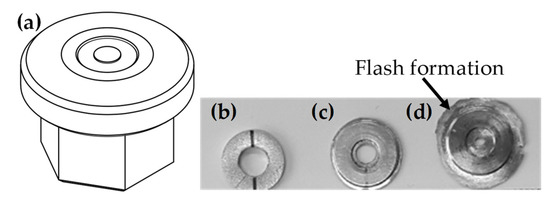
Figure 2.
(a) 3D drawing of one part of the mold and (b–d) shows the images of commercially pure al sample at different stages of processing, i.e., initial, compressed and after SPD.
3. Result and Discussion
Commercial purity Al was selected as the study material, since plenty of results of static HPT tests were available on this material. The as received material was in the form of cast blocks, having a composition: Al-0.28%Fe-0.05%Si-0.05%Cu (wt %). The material was then cold rolled and annealed to generate the recrystallized structure having stress-free large grains. The samples of outer diameter of 11 mm and an internal diameter of 5 mm, were produced from the annealed sheets.
In order to relate the structure and properties of the DHPT processed material, with that of HPT processed samples, HPT experiments were conducted on the disk shaped specimen of 15 mm diameter. The HPT processing was conducted at small rotations of 10, 15, 20, and 25 deg. The deformed samples from both HPT and DHPT processing were investigated for their microstructural characteristics and mechanical properties using orientation imaging microscopy (OIM) and microhardness measurements, respectively. The geometry and reference system common for both disk- and ring-specimens are shown in Figure 3, together with the surface used for optical and OIM investigations. For micro-hardness measurements, the r-θ plane was considered.
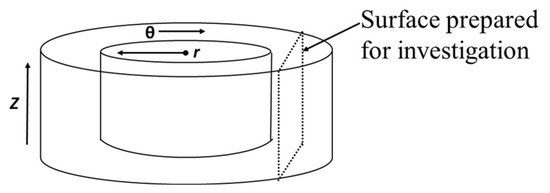
Figure 3.
Geometry of the ring-specimen with θ being the shear direction (SD), r the radial direction (RD) and Z the shear plane normal (SPN). The indicated θ-Z plane was prepared for optical and OIM investigation.
Figure 2b–d shows images of samples in initial, compressed and shear deformed conditions. It is interesting to note that the final deformed sample shows substantial flash formation around the periphery, and subsequently its presence provides the hydrostatic pressure condition during shear deformation by restricting further outflow of the material from mold cavity. Figure 4 gives an idea about the evolution of structure as well as hardness in HPT and DHPT materials. In HPT sample deformed to a strain of 0.21, the mean grain size hardly changed from that in annealed condition (~85 μm), whereas DHPT materials shows clear fragmentation in the form of decreased grain size with increasing shear strain. Commensurate with the microstructure observation, hardness evolution in DHPT materials occurs at a faster pace than in HPT samples.
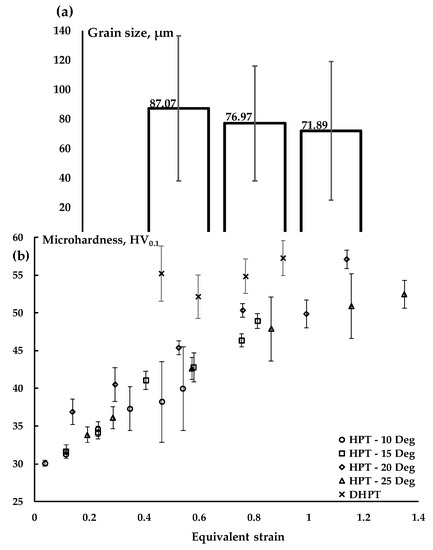
Figure 4.
(a) Shows grain size obtained in different processing conditions and (b) is a plot between equivalent strain and measured microhardness values for HPT and DHPT samples.
4. Summary
In present work, a novel dynamic SPD facility, named as DHPT, is introduced wherein HPT like deformation conditions generate the SPD deformation while SHTB like mechanism delivers the deformation at high strain rate, onto the material held under hydrostatic pressure conditions. Commercially pure aluminum samples were deformed via both HPT and DHPT, and it was found that DHPT material fragments into smaller grains at a faster pace than that of HPT deformed samples. Accordingly, higher hardness values were observed in DHPT processed samples than in HPT samples. Future work involves introducing higher shear strains in the material and obtain further fragmentation in the structure and it would be interesting to see the onset and behavior of material at the saturation limits, when compared with the static HPT processed material.
Author Contributions
P.V. conceived and developed the principle of the setup, and designed the setup, L.K. assisted with the microstructural data analysis; while H.L. performed the HPT and DHPT experiments, the microstructural observations and hardness tests, and wrote the paper.
Acknowledgments
The authors would like to acknowledge the Interuniversity Attraction Poles Program (IUAP) of the Federal Science Policy of Belgium and the partners of IUAP-VII-project P7/21 ‘Multiscale mechanics of interface dominated materials’.
Conflicts of Interest
The authors declare no conflict of interest. The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
References
- Valiev, R.Z.; Langdon, T.G. Achieving exceptional grain refinement through severe plastic deformation: New approaches for improving the processing technology. Metall. Mater. Trans. A 2011, 42, 2942–2951. [Google Scholar] [CrossRef]
- Estrin, Y.; Vinogradov, A. Extreme grain refinement by severe plastic deformation: A wealth of challenging science. Acta Mater. 2013, 61, 782–817. [Google Scholar] [CrossRef]
- Renk, O.; Hohenwarter, A.; Wurster, S.; Pippan, R. Direct evidence for grain boundary motion as the dominant restoration mechanism in the steady-state regime of extremely cold-rolled copper. Acta Mater. 2014, 77, 401–410. [Google Scholar] [CrossRef] [PubMed]
- Gray, G.T. High-strain-rate deformation: Mechanical behavior and deformation substructures induced. Annu. Rev. Mater. Res. 2012, 42, 285–303. [Google Scholar] [CrossRef]
- Li, Y.S.; Zhang, Y.; Tao, N.R.; Lu, K. Effect of the zener-hollomon parameter on the microstructures and mechanical properties of Cu subjected to plastic deformation. Acta Mater. 2009, 57, 761–772. [Google Scholar] [CrossRef]
- Ahn, D.-H.; Lee, D.J.; Kang, M.; Park, L.J.; Lee, S.; Kim, H.S. Bi-modal structure of copper via room-temperature partial recrystallization after cryogenic dynamic compression. Metall. Mater. Trans. A 2016, 47, 1600–1606. [Google Scholar] [CrossRef]
- Khamsuk, S.; Park, N.; Adachi, H.; Terada, D.; Tsuji, N. Evolution of ultrafine microstructures in commercial purity aluminum heavily deformed by torsion. J. Mater. Sci. 2012, 47, 7841–7847. [Google Scholar] [CrossRef]
- Chiem, C.Y.; Duffy, J. Strain rate history effects and observations of dislocation substructure in aluminum single crystals following dynamic deformation. Mater. Sci. Eng. 1983, 57, 233–247. [Google Scholar] [CrossRef]
- Inomoto, H.; Fujiwara, H.; Ameyama, K. Characteristics of Nano Grain Structure in SPD-PM Processed AISI304L Stainless Steel Powder; Wiley: Vienna, Austria, 2002. [Google Scholar]
- Brown, T.L.; Saldana, C.; Murthy, T.G.; Mann, J.B.; Guo, Y.; Allard, L.F.; King, A.H.; Dale Compton, W.; Trumble, K.P.; Chandrasekar, S. A study of the interactive effects of strain, strain rate and temperature in severe plastic deformation of copper. Acta Mater. 2009, 57, 5491–5500. [Google Scholar] [CrossRef]
- Xu, P.; Luo, H.; Han, Z.; Zou, J. Tailoring a gradient nanostructured age-hardened aluminum alloy using high-gradient strain and strain rate. Mater. Des. 2015, 85, 240–247. [Google Scholar] [CrossRef]
- Baker, W.E.; Yew, C.H. Strain-rate effects in the propagation of torsional plastic waves. J. Appl. Mech. 1966, 33, 917–923. [Google Scholar] [CrossRef]
- Meyers, M.A. Dynamic Behavior of Materials; John Wiley & Sons, Inc.: New York, NY, USA, 1994. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).