Considerations of Failure Analysis in a Multi-Layered Composite Structure under Thermomechanical Loading †
Abstract
1. Introduction
2. Mathematical Modeling
3. Failure Analysis Criteria
3.1. Tsai-Hill Failure Criterion
3.2. Tsai-Wu Failure Criterion
3.3. Hoffman Failure Criterion
4. Numerical Experiment
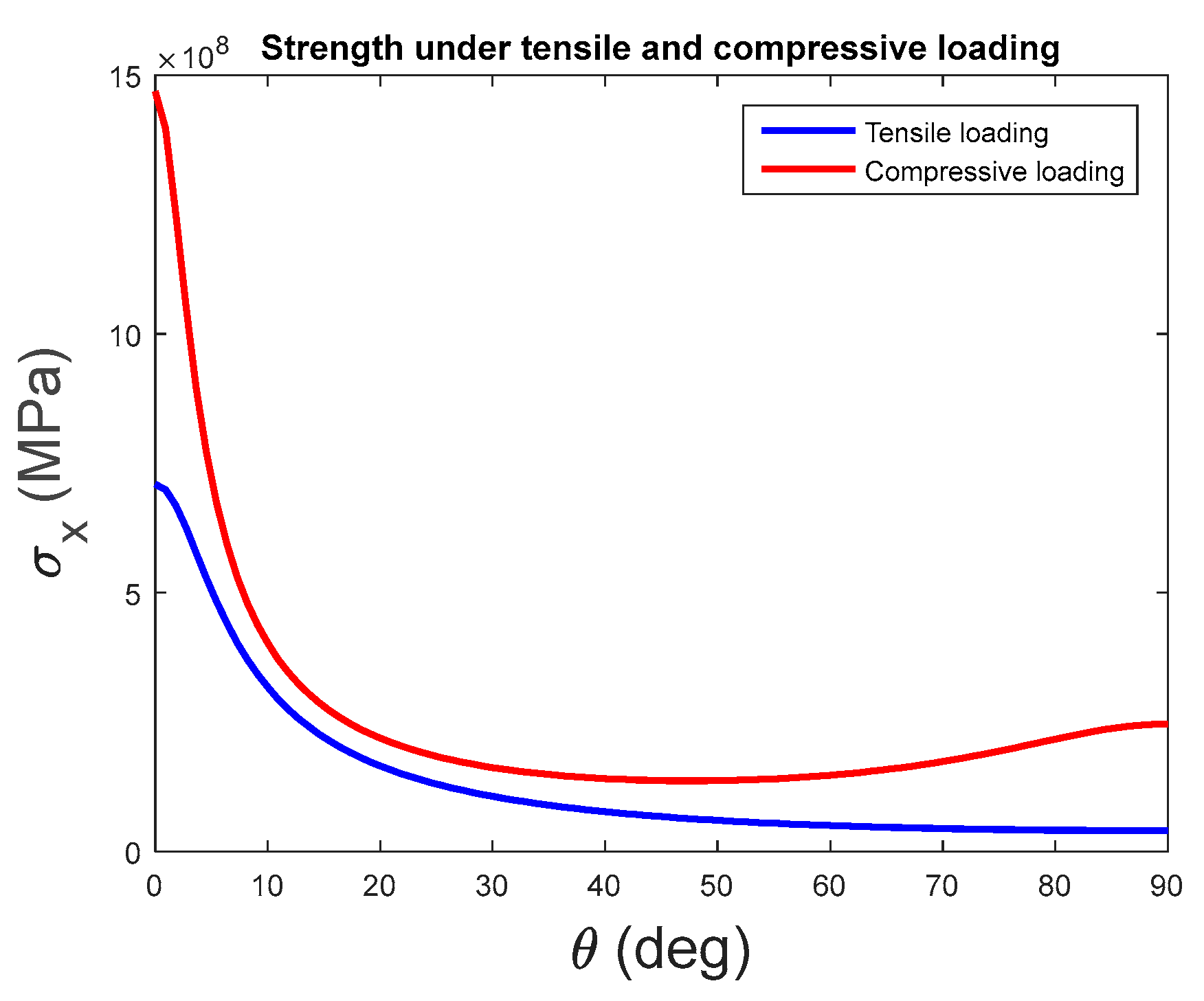
5. Results and Discussion
6. Conclusions
References
- Zweben, C. Wiley Online Library (Composite Materials). Available online: http://onlinelibrary.wiley.com/doi/10.1002/9781118985960.meh110/pdf (accessed on 20 September 2016).
- Pawar, P.M.; Ganguli, R. On the effect of matrix cracks in composite Helicopter Rotor Blades. Compos. Sci. Technol. 2005, 65, 581–594. [Google Scholar] [CrossRef]
- Massabo, R.; Campi, F. Thermomechanical loading of laminates with imperfect interfaces. Procedia Eng. 2014, 88, 34–41. [Google Scholar] [CrossRef]
- Huang, Z.H. Modeling strength of multidirectional laminates under thermo-mechanical loads. J. Compos. Mater. 2011, 35, 281–304. [Google Scholar] [CrossRef]
- Dupir, I.; Țăranu, N.; Axinte, A. Effect of stacking sequence on the coefficients of mutual influence of composite laminates. IOP Conf. Ser. Mater. Sci. Eng. 2016, 161, 012052. [Google Scholar] [CrossRef]
- Greif, R.; Chapon, E. Investigation of successive failure modes in graphite/epoxy laminated composite beams. J. Reinf. Plast. Compos. 1993, 12, 602–603. [Google Scholar] [CrossRef]
- Yang, C.; Jiao, G.; Guo, H. Failure criteria for C/SiC composites under plane stress state. Theor. Appl. Mech. Lett. 2014, 4, 021007. [Google Scholar] [CrossRef][Green Version]
- Uttam, S.; Koruche, S.F. Application of Classical Lamination Theory and Analytical Modeling of Laminates. Int. Res. J. Eng. Technol. 2015, 2, 958–965. [Google Scholar]
- Sundararaman, S.; Hu, J.; Chanrashekhara, K. Thermomechanical analysis of composite cylinders for hydrogen storage. In Proceedings of the SAMPE Conferene, Baltimore, MD, USA, 3–7 June 2007; pp. 1–12. [Google Scholar]
- Nettles, A.T. Basic Mechanics of Laminated Composite Plates; NASA: Huntsville, AL, USA, 1994. [Google Scholar]
- Engblom, J.J. Stress and Failure Analysis of Laminated Composite Structures; PDH Center: Faifax, VA, USA, 2012. [Google Scholar]
- Voyiadjis, G.Z.; Kattan, P.I. Mechanics of Composite Materials with MATLAB, 2005th ed.; Springer: Berlin, Germany, 2005; p. 189. [Google Scholar]
- Ryan, C. An Intelligible Software (CFA) Approach for Fiber-Reinforced Laminate Failure Analysis Including a Piecewise Representation of the Tsai-Wu Failure Criterion Using Excel and MatLab. Master’s Thesis, Master of Science, Schmidt Embry-Riddle Aeronautical University, Daytona Beach, FL, USA, 2009. [Google Scholar]
- Arafat, I.K. Progressive Failure Analysis of Laminated Composite Structures. Ph.D. Thesis, Doctor of Philosophy, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 2015. [Google Scholar]
- Hallquist, J.O.; LS-Dyna, L.S. Theoretical Manual; Livermore Software Technology Corporation: Livermore, CA, USA, 2005. [Google Scholar]
- Chang, F.K.; Chang, K.Y. A progressive damage model for laminated composites containing stress concentration. J. Compos. Mater. 1987, 21, 834–855. [Google Scholar] [CrossRef]

| Stiffness Properties | |||||||
| 0.28 | |||||||
| Strength Properties | |||||||
| Tsai-Hill | Tsai-Wu | Hoffmann |
|---|---|---|
| −0.7441 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nyambeni, N.; Mabuza, B.R. Considerations of Failure Analysis in a Multi-Layered Composite Structure under Thermomechanical Loading. Proceedings 2018, 2, 447. https://doi.org/10.3390/ICEM18-05329
Nyambeni N, Mabuza BR. Considerations of Failure Analysis in a Multi-Layered Composite Structure under Thermomechanical Loading. Proceedings. 2018; 2(8):447. https://doi.org/10.3390/ICEM18-05329
Chicago/Turabian StyleNyambeni, Ngeletshedzo, and Boy Raymond Mabuza. 2018. "Considerations of Failure Analysis in a Multi-Layered Composite Structure under Thermomechanical Loading" Proceedings 2, no. 8: 447. https://doi.org/10.3390/ICEM18-05329
APA StyleNyambeni, N., & Mabuza, B. R. (2018). Considerations of Failure Analysis in a Multi-Layered Composite Structure under Thermomechanical Loading. Proceedings, 2(8), 447. https://doi.org/10.3390/ICEM18-05329




