Assessment of Environmental Effects for Vibration-Based Damage Detection of Historic Masonry Towers ^†

Abstract

The paper firstly focuses on selected results obtained by continuously monitoring the dynamic response of three ancient masonry towers in Italy in order to highlight the possible effects of changing temperature on the resonant frequencies; subsequently, the removal of environmental effects (needed for an effective performance assessment and damage detection) is addressed and discussed using the data acquired on a challenging historic tower.

1. Introduction

Structural Health Monitoring (SHM) is generally defined as a multi-disciplinary process involving: (a) the repeated or continuous measurement of the response of a structural system through arrays of appropriate sensors; (b) the extraction from measured data of features, which are representative of the health condition and (c) the statistical analysis of these features to detect any novelty or abnormal change in the investigated system.

Among the different SHM approaches, the one based on the continuous measurement of the dynamic response is especially suitable to ancient towers as those structures are generally sensitive to ambient excitation and exhibit a cantilever-like dynamic behavior, so that the successful monitoring of the dynamic characteristics can be obtained by permanently installing a few high-sensitivity accelerometers (or seismometers) in the upper part of the building [1,2,3,4,5]. On the other hand, masonry towers are very common Cultural Heritage buildings in Italy and often exhibit high vulnerability to seismic actions, as it has been dramatically testified also by the recent Italian events, such as the ones hitting the Emilia region in 2012 and the Central Italy in 2016.

The use of a limited number of sensors and automated identification of modal parameters in SHM implies the choice of resonant frequencies as features to be assumed as representative of the structural condition. Since the modal frequencies are also sensitive to factors other than structural changes—such as the environmental conditions—and especially the temperature might affect the variation of resonant frequencies in ancient towers [1,2,3,4,5,6], an effective approach of damage detection and SHM should include the removal (or minimization) of the temperature effects on identified frequencies.

The paper firstly describes the typical mechanisms governing the environmentally-induced changes in the natural frequencies of ancient towers, as highlighted during the continuous dynamic monitoring of three historic towers in Italy. Subsequently, in order to mitigate the effects of environmental parameters on resonant frequencies, the application of the multiple linear regression (MLR) [7] and the principal component analysis (PCA) [8] tools is exemplified using one year of frequency data collected on the Santa Maria del Carrobiolo bell-tower [5].

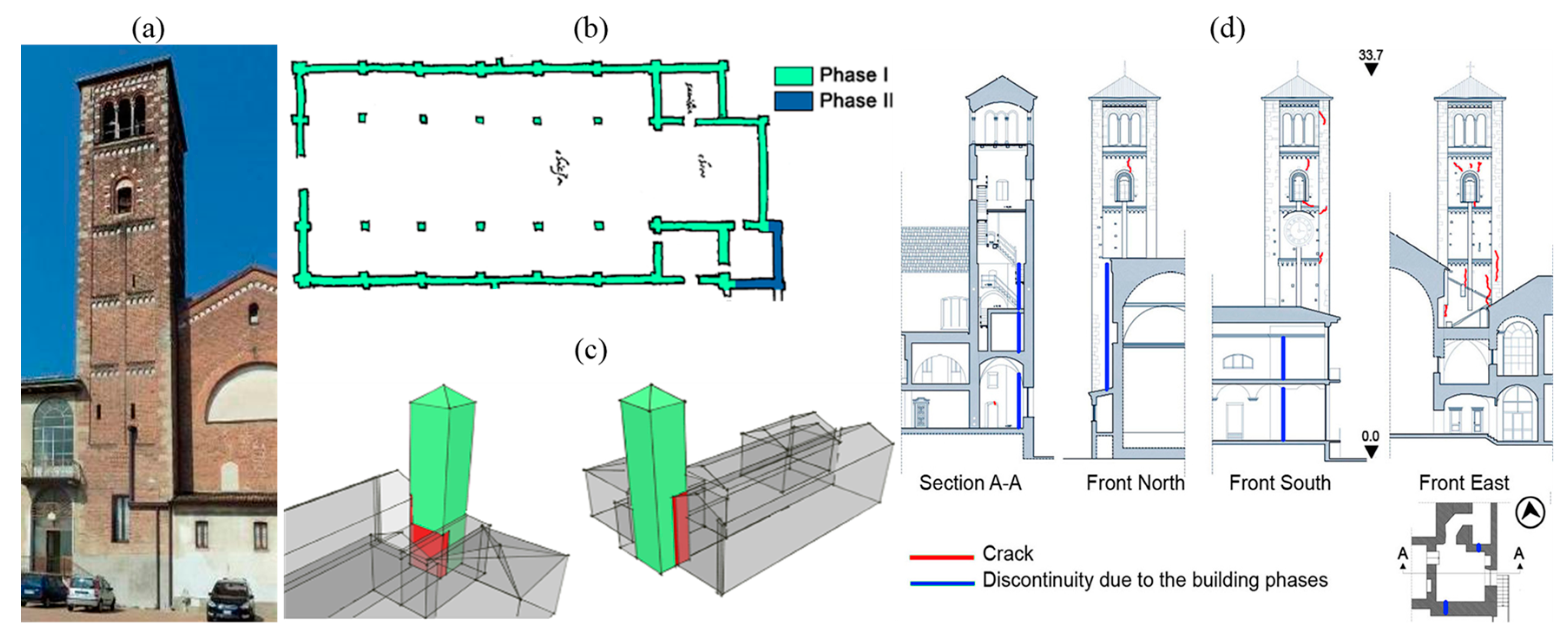
2. The Influence of Environmental Changes on the Natural Frequencies of Ancient Towers

The environmental parameters affect the dynamic characteristics of masonry towers and buildings in a peculiar way, which seems to be different from that of concrete, steel and pre-stressed concrete structures. The continuous dynamic monitoring carried out by the authors on various towers—such as the Gabbia tower in Mantua ([2], Figure 1a), the San Vittore bell-tower in Arcisate ([3], Figure 1b) and the Santa Maria del Carrobiolo bell-tower in Monza ([5], Figure 2)—allows to conclude that different temperature-driven effects on frequency changes can be observed:

• The increase of natural frequencies with increased temperature. This behavior, observed in all studies of masonry towers [1,2,3,4,5,6] can be explained by the closure of superficial cracks and minor masonry discontinuities induced by the thermal expansion of materials. The correlation between frequency and temperature tends to be essentially linear when the temperature exceeds 10–15 °C but non linear effects are detected in the lower range of temperatures;
• Around the freezing conditions, the natural frequencies rapidly and significantly increase with decreased temperature [3,4]. This behavior is conceivably related to the freezing of the structural system (including its foundation) and to the presence of ice, which fills and closes the cracks, causing a temporary stiffening of the structure;
• Some effects of the increased temperature at the local level (such as the increase of thrust exerted by inclined structural elements [2] or the slackening of ties [4,5]) might induce significant frequency reduction (or slight overall change) with increased temperature. In the authors’ opinion, this last aspect deserves further investigation as a frequency decrease with increasing temperature could be an easy-to-evaluate symptom of an unsatisfactory state of preservation of the historic building.

Furthermore, effects of relative humidity (i.e., decrease of natural frequencies associated to water absorption of load-bearing walls during the raining season) are occasionally reported in the literature [1].

3. Removal of Environmental Effects

In order to exemplify the removal of the temperature effects from the automatically identified natural frequencies, the Santa Maria del Carrobiolo bell-tower [5] (Figure 2) is considered.

The tower (Figure 2a), about 33.7 m high, is built in solid brick masonry and has nearly square plan (5.93 m × 5.70 m); the thickness of the load bearing walls slightly decreases from 70 cm at the ground level to 58 cm at the top. The tower belongs to a religious complex including also a church, a monastery, an oratory and other minor buildings, which were erected at different times.

Historical documents testify that the construction of the church and monastery dates to the 13th century, whereas the bell-tower was completed in 1339 (Figure 2b). The sequence of the construction stages has been confirmed by visual inspection of the masonry discontinuities: (a) the North and West sides of the tower are directly supported by the load-bearing walls of the apse and the right aisle of the church; (b) the Southern and Eastern load-bearing walls of the tower are continuous from the ground to the roof but do not exhibit any mechanical connections with the walls of the church (Figure 2c,d). Moreover, several cracks cut the entire wall thickness, mainly at the level below the belfry (Figure 2d), and a metallic tie-rod opposes to the opening of a deep crack on the Western wall of the bell-tower [5].

Ambient vibration tests (AVTs) were carried out on 23 September 2015 to evaluate the baseline dynamic characteristics of the tower before the installation of a continuous dynamic monitoring system in the building.

The accelerometers’ layout adopted in the AVT is schematically illustrated in Figure 3 and allows to identify both the bending modes in the N–S and E–W direction and the torsion modes. The identified mode shapes are presented in Figure 3 and reveal peculiar dynamic characteristics of the tower, that are conceivably related to the structural arrangement and construction sequence of the building (Figure 2). In more details, closely spaced modes with similar mode shapes were clearly identified, so that the sequence of identified modes turns out to be very different from the expected regular series of two bending modes (one for each principal plane of the structure) and one torsion mode. The identified sequence of vibration modes (Figure 3) consists of: (a) the fundamental mode (f_x1 = 1.92 Hz, Figure 3a), involving dominant bending in the E–W direction; (b) two bending modes in the N–S direction, that are characterized by closely spaced natural frequencies (f_y1 = 2.01 Hz and f*_y1 = 2.37 Hz) and very similar mode shapes (Figure 3b,c); (c) another mode of dominant bending, again in the N–S direction (f_y2 = 4.14 Hz, Figure 3d); (d) two torsion modes (f_T1 = 4.55 Hz and f_T2 = 5.25 Hz) with very similar mode shapes (Figure 3e,f); (e) the last mode (f_x2 = 7.53 Hz, Figure 3g), involving almost pure bending in the E–W direction.

A continuous dynamic monitoring system (Figure 4a) is installed in the tower since 22 October 2015 and includes 4 MEMS accelerometers (Kistler model 8330A3, 1.2 V/g sensitivity, ±3.00 g peak acceleration, 1.3 µg resolution and 0.4 µg/√Hz rms noise density), one Ethernet carrier with NI 9234 data acquisition module and one local PC for the management of the continuous acquisition and the data storage. Data are recorded at 200 Hz and stored on the local PC in separate files of 60 min. It should be noticed that the instrumented level—although not optimal for the identification of all modes—is the higher one suitable to the installation of a continuous dynamic monitoring system.

The monitoring system also includes 5 temperature sensors—denoted as T_0N, T_1E, T_2E, T_2W and T_S in Figure 4a—so that a relatively dense representation of the temperature conditions of the tower is achieved.

The collected acceleration data are processed through a series of routines developed in the LabVIEW environment and comprising the following tasks: (a) signal pre-processing with de-trending and de-spiking of the raw data; (b) automatic detection and extraction of the time series associated to swinging of bells and numerical integration to estimate velocity time histories; (c) creation, for each 1-h dataset, of one time window containing only the ambient vibration response; (d) low-pass filtering and decimation of the each set of “bell-free” time-series, which were reduced to a uniform time window of 3000 s for the application of the modal identification tools.

The modal parameters of the bell-tower were extracted from each 3000 s acceleration dataset using a fully automated procedure [5].

Figure 4b,c present the evolution of the identified modal frequencies in the first year of continuous dynamic monitoring (i.e., from 22 October 2015 to 21 October 2016). The results summarized in Figure 4b,c allow the following comments:

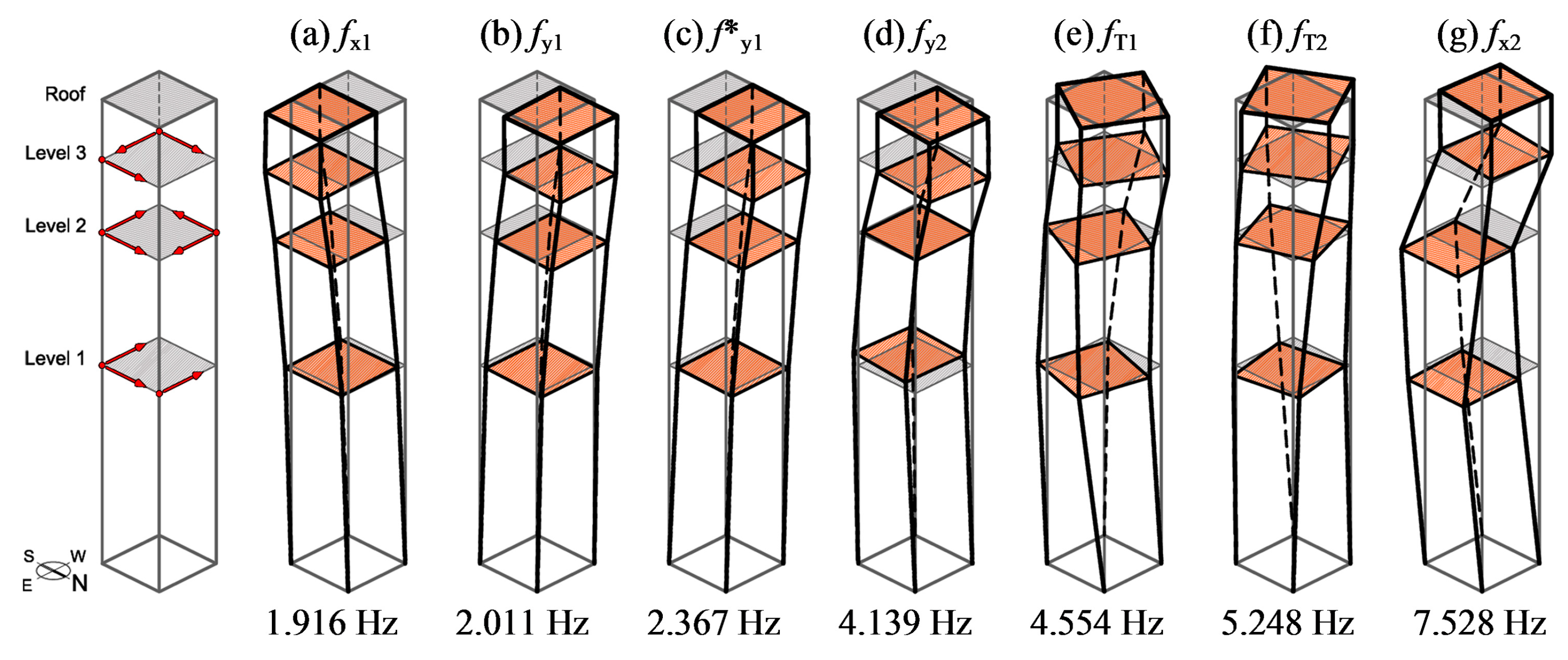
• Notwithstanding the low level of the ambient excitation, 4 normal modes were identified with high occurrence and accuracy;
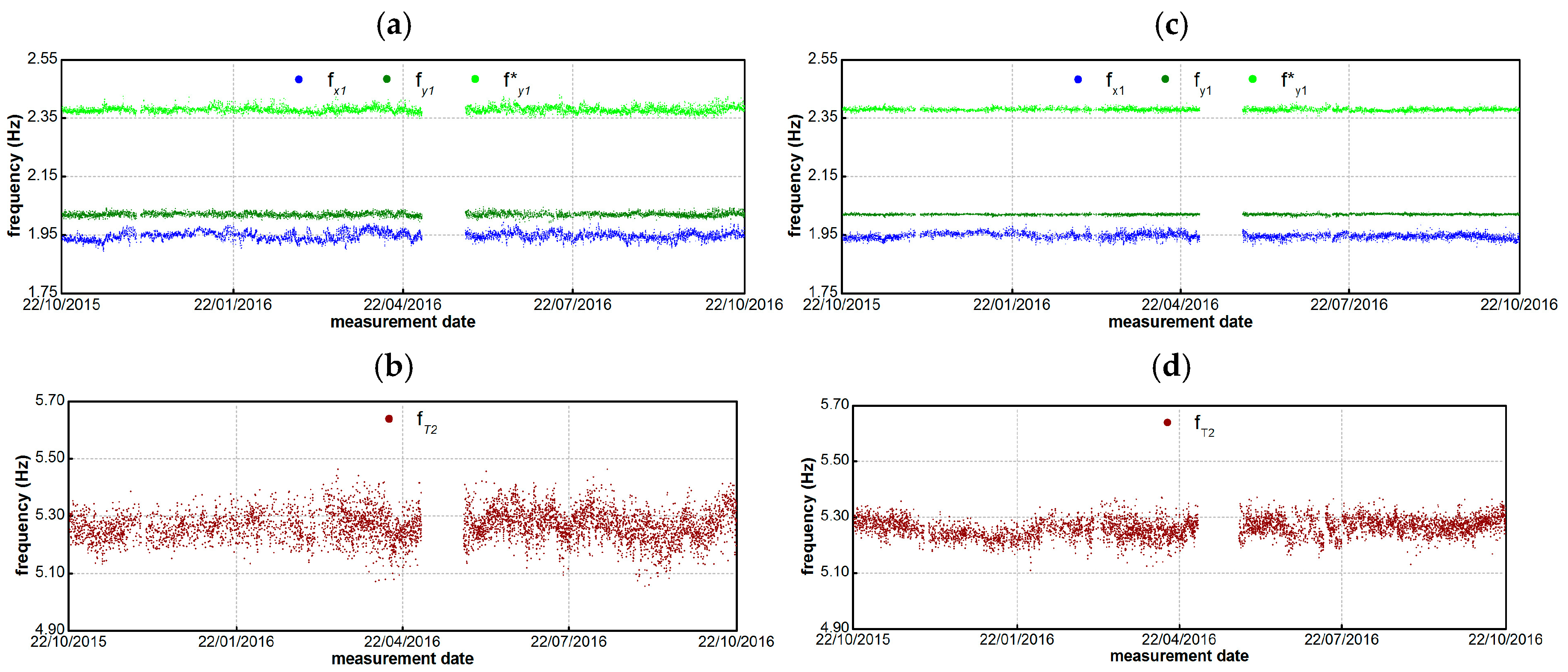
• The natural frequency of modes f_x1 and f_T2 exhibits significant increase in Spring and Summer period;
• On the contrary, the natural frequency of modes f_y1 and f*_y1 exhibits very limited variation, with the standard deviation being equal to 0.009 and 0.015 Hz, respectively. For those modes, the frequency trend increase with increased temperature is conceivably balanced by the loss of tension in the metallic tie-rod placed on the West side and connecting the North and South load-bearing walls of the tower;
• As shown in Figure 4b, the natural frequencies of the two lower modes f_x1 and f_y1 exhibit crossing in Summer months. To the best of the authors’ knowledge, this behavior has not been observed before on masonry towers and conceivably depends on the different effect exerted by the temperature on the natural frequencies of the two modes. Furthermore, the mode shape of both modes f_x1 and f_y1 tends to hybridize when crossing occurs: in other words, the two modes tend to involve biaxial bending in both the main E–W and N–S directions when the natural frequencies become very close to each other.

Figure 4b,c suggests that the natural frequencies of the bell-tower are affected by environmental factors in a way that is likely more significant than variations induced by a small damage. As natural frequencies are commonly used in SHM, different procedures have been proposed in the literature to mitigate the effects of environmental factors. When the environmental parameters are measured, regression and interpolation analyses [1,2,3,4,6,7] might be performed to approximately estimate supervised learning algorithms between the directly measured environmental parameters and the natural frequencies observed in a specified reference (or “training”) period. Otherwise, unsupervised learning algorithms—for instance based on the principal component analysis (PCA) [5,6,8]—could be used to account for the different unmeasured factors, that affect the frequency variation during a training period, as embedded variables. Both supervised and unsupervised learning algorithms are usually coupled with novelty analysis (see e.g., [2,3,6]) of the frequency residual errors to detect the occurrence of structural anomalies.

Among the different procedures reported in the literature to remove the environmental effects from identified frequency data, the well-known multiple linear regression (MLR) [7] has been firstly adopted. This choice is motivated by the availability of multiple temperature measurements (Figure 4a), as well as by the possibility of accounting for possible non-linear dependence on temperature. More specifically, each response variable y_k (i.e., the i-th resonant frequency) at current time k has been modeled using a second order polynomial and 3 temperatures T_0N, T_2W and T_S as predictors (input variables):

y_k = β₀ + β₁ T_0N,k + β₂ T_2W,k + β₃ T_S,k + β₄ (T_0N,k)² + β₅ (T_2W,k)² + β₆ (T_S,k)² + ε_k

(1)

Subsequently, the PCA [8] has been applied to remove the variability due to changes in the environment. This approach—generally adopted to reduce the dimensions of a data set, while retaining the characteristics of the original data mostly contributing to its variance—represents an attractive option because it works without requiring any measurement of environmental factors or variable selection scheme.

A comparison of the performance of the two investigated approaches is presented in Figure 5 through the time evolution of the cleaned observations. Although at first glance the two procedures seem to provide a similar performance, it should be noticed that the cleaned observations provided by the MLR (Figure 5a,b) still exhibit some correlation, meaning that they are still affected by common factors; on the other hand, the PCA leads to better cleaned frequencies (Figure 5c,d).

4. Conclusions

Selected results of the continuous dynamic monitoring of three historic towers [2,3,5] have been recalled in the paper to highlight the possible different effects exerted from changing temperature on the time evolution of continuously identified modal frequencies.

Furthermore, the removal of the temperature effects has been exemplified by using the MLR [7] and the PCA [8] methods. The PCA-based regression turned out to be an effective tool to mitigate the environmental effects on automatically identified frequencies, in spite of the relatively small number of monitored frequencies.