Use of Spectral Entropy for Damage Detection in Masonry Buildings in the Presence of Mild Seismicity †
Abstract
:1. Introduction
2. Materials and Methods
3. Case Studies
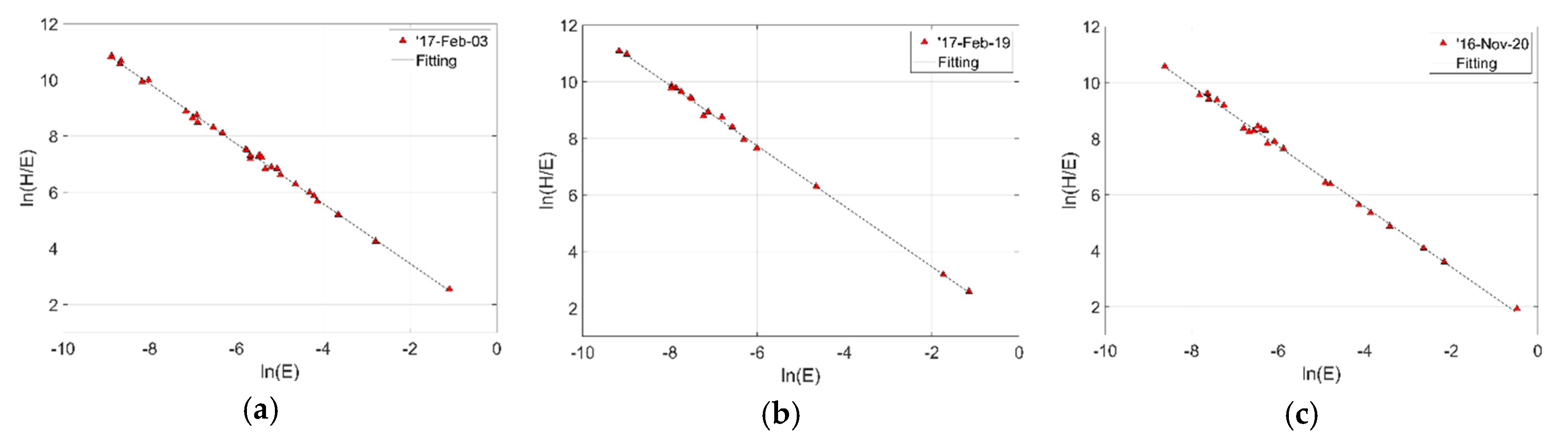
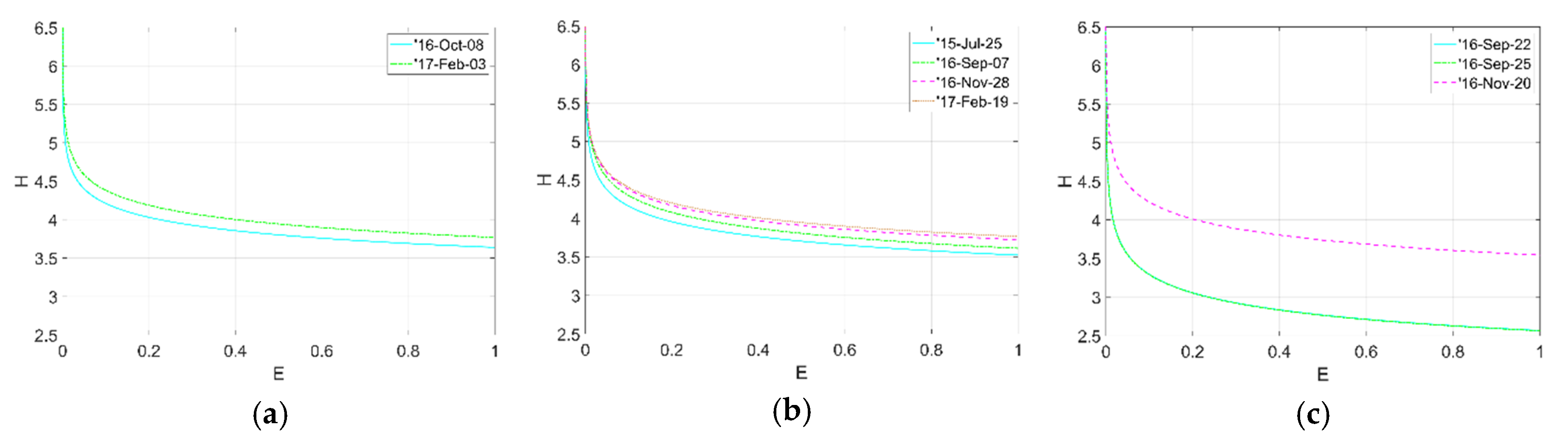
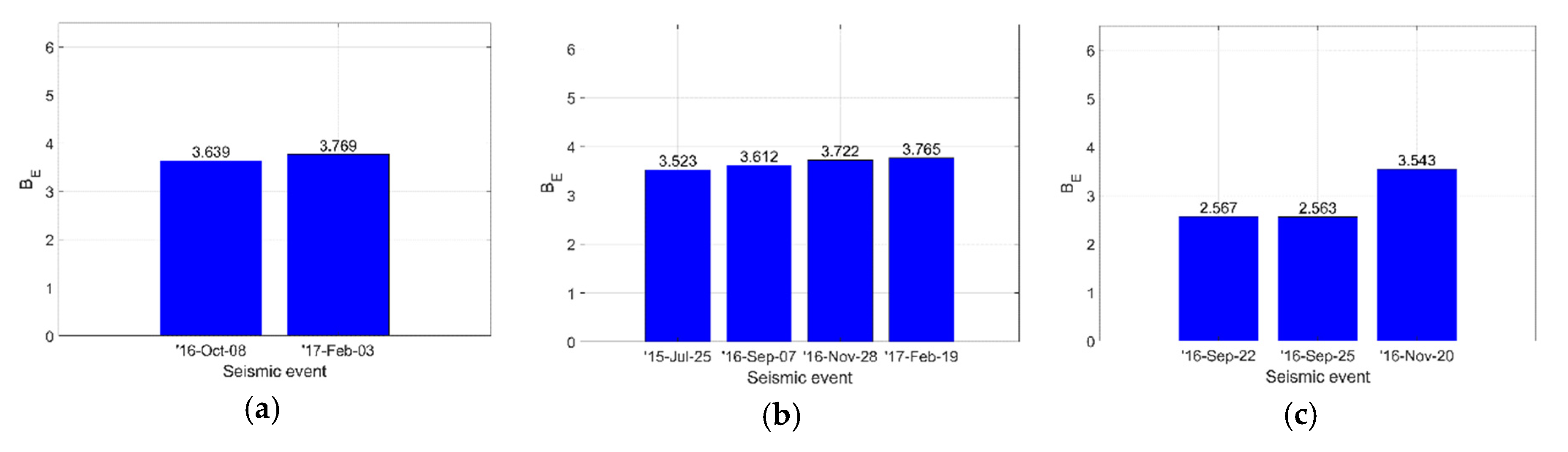
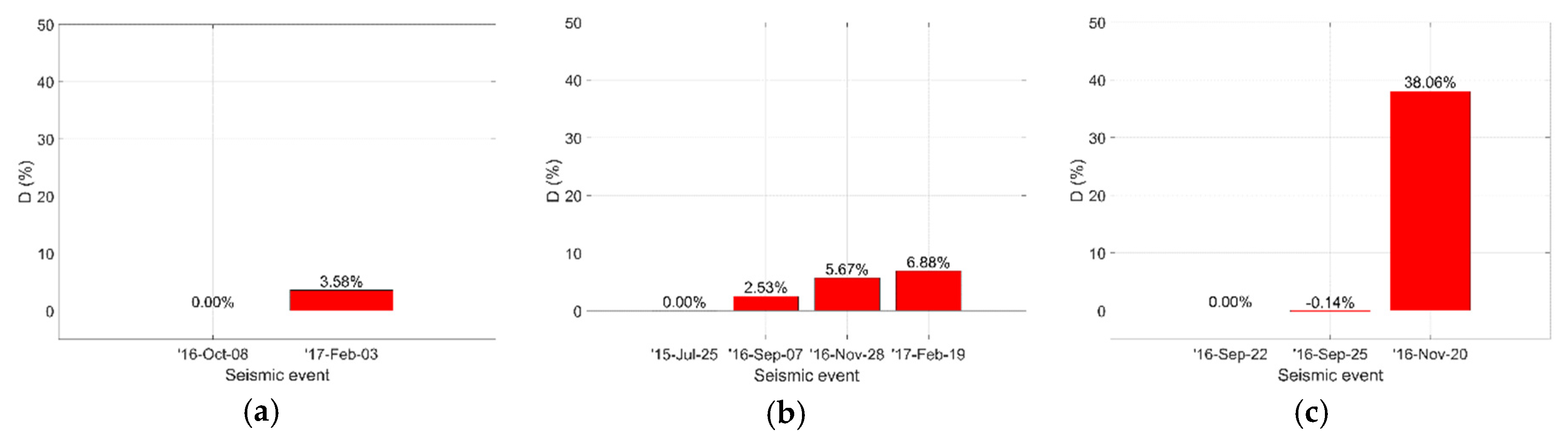
4. Results and Discussion
5. Conclusions
Author Contributions
Acknowledgments
References
- Masciotta:, M.G.; Ramos, L.; Lourenço, P. The importance of structural monitoring as a diagnosis and control tool in the restoration process of heritage structures: A case study in Portugal. J. Cult. Herit. 2017, 27, 36–47. [Google Scholar] [CrossRef]
- Powell, G.; Percival, I. A spectral entropy method for distinguishing regular and irregular motion of Hamiltonian systems. J. Phys. A Gener. Phys. 1979, 12, 2053–2071. [Google Scholar] [CrossRef]
- Ceravolo, R.; Matta, M.; Quattrone, A.; Fragonara, L.Z. Amplitude dependence of equivalent modal parameters in monitored buildings during earthquake swarms. Earthq. Eng. Struct. Dyn. 2017, 46, 2399–2417. [Google Scholar] [CrossRef]
- Sharma, V.; Parey, A. Gearbox fault diagnosis using RMS based probability density function and entropy measures for fluctuating speed conditions. Struct. Health Monit. 2017, 16, 682–695. [Google Scholar] [CrossRef]
- Melia, U.; Claria, F.; Vallverdu, M.; Caminal, P. Measuring instantaneous and spectral information entropies by shannon entropy of choi-williams distribution in the context of electroencephalography. Entropy 2014, 16, 2530–2548. [Google Scholar] [CrossRef]
- Dolce, M.; di Bucci, D. Comparing recent Italian earthquakes. Bull. Earthq. Eng. 2017, 15, 497–533. [Google Scholar] [CrossRef]
- Penna, A.; Morandi, P.; Rota, M.; Manzini, C.; da Porto, F.; Magenes, G. Performance of masonry buildings during the Emilia 2012 earthquake. Bull. Earthq. Eng. 2014, 12, 2255–2273. [Google Scholar] [CrossRef]
- Sorrentino, L.; Cattari, S.; da Porto, F.; Magenes, G.; Penna, A. Seismic behaviour of ordinary masonry buildings during the 2016 central Italy earthquakes. Bull. Earthq. Eng. 2018. [Google Scholar] [CrossRef]
- Di Ludovico, M.; Digrisolo, A.; Graziotti, F.; Moroni, C.; Belleri, A.; Caprili, S.; Carocci, C.; Dall’Asta, A.; de Martino, G.; de Santis, S.; et al. The contribution of ReLUIS to the usability assessment of school buildings following the 2016 central Italy earthquake. Boll. Geofis. Teor. Appl. 2017, 58, 353–376. [Google Scholar]
- Dolce, M.; Nicoletti, M.; de Sortis, A.; Marchesini, S.; Spina, D.; Talanas, F. Osservatorio sismico delle strutture: The Italian structural seismic monitoring network. Bull Earthq. Eng. 2015, 15, 621–641. [Google Scholar] [CrossRef]
- Gruppo di Lavoro INGV sul terremoto di Amatrice. Secondo rapporto di sintesi sul Terremoto di Amatrice Ml 6.0 del 24 Agosto 2016 (Italia Centrale). 2016. [Google Scholar] [CrossRef]
- Ceravolo, R.; de Lucia, G.; Matta, E.; Quattrone, A.; Fragonara, L.Z. Equivalent modal parameters in monitored buildings during the recent Italian seismic events. In Proceedings of the XVII Convegno ANIDIS—L'ingegneria sismica in Italia, Pistoia, Italy, 17–21 September 2017. [Google Scholar]
- Ceravolo, R.; De Lucia, G.; Lenticchia, E.; Miraglia, G. Use of combinatorial optimisation strategies for model updating of monitored buildings. In Proceedings of the 10th International Masonry Conference, Milan, Italy, 9–11 July 2018. [Google Scholar]


| Main Shock | Building | PGA-x [g] | PGA-y [g] | PGA-z [g] |
|---|---|---|---|---|
| 2016-Aug-24a (01:36 UTC) | Fabriano | 0.04 | 0.05 | 0.03 |
| Pizzoli | 0.08 | 0.09 | 0.06 | |
| Visso | 0.33 | 0.32 | 0.13 | |
| 2016-Oct-26a (17:10 UTC) | Fabriano | 0.03 | 0.03 | 0.02 |
| Pizzoli | 0.02 | 0.02 | 0.02 | |
| Visso | 0.29 | 0.21 | 0.41 | |
| 2016-Oct-26b (19:18 UTC) | Fabriano | 0.08 | 0.09 | 0.08 |
| Pizzoli | 0.02 | 0.03 | 0.02 | |
| Visso | 0.36 | 0.48 | 0.31 | |
| 2016-Oct-30 (06:40 UTC) | Fabriano | 0.05 | 0.04 | 0.05 |
| Pizzoli | 0.11 | 0.11 | 0.06 | |
| Visso | 0.29 | 0.30 | 0.33 | |
| 2017-Jan-18b (10:14 UTC) | Fabriano | 0.01 | 0.01 | 0.00 |
| Pizzoli | 0.11 | 0.10 | 0.08 | |
| Visso | - | - | - |
| Fabriano | Pizzoli | Visso | |||||||
| Seismic event | 2016 Oct-08 | 2017 Feb-03 | 2015 Jul-25 | 2016 Sep-07 | 2016 Nov-28 | 2017 Feb-19 | 2016 Sep-22 | 2016 Sep-25 | 2016 Nov-20 |
| a | −1.063 | −1.065 | −1.072 | −1.075 | −1.070 | −1.068 | −1.108 | −1.108 | −1.077 |
| b | 1.291 | 1.326 | 1.259 | 1.284 | 1.314 | 1.325 | 0.942 | 0.941 | 1.265 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ceravolo, R.; Lenticchia, E.; Miraglia, G. Use of Spectral Entropy for Damage Detection in Masonry Buildings in the Presence of Mild Seismicity. Proceedings 2018, 2, 432. https://doi.org/10.3390/ICEM18-05288
Ceravolo R, Lenticchia E, Miraglia G. Use of Spectral Entropy for Damage Detection in Masonry Buildings in the Presence of Mild Seismicity. Proceedings. 2018; 2(8):432. https://doi.org/10.3390/ICEM18-05288
Chicago/Turabian StyleCeravolo, Rosario, Erica Lenticchia, and Gaetano Miraglia. 2018. "Use of Spectral Entropy for Damage Detection in Masonry Buildings in the Presence of Mild Seismicity" Proceedings 2, no. 8: 432. https://doi.org/10.3390/ICEM18-05288
APA StyleCeravolo, R., Lenticchia, E., & Miraglia, G. (2018). Use of Spectral Entropy for Damage Detection in Masonry Buildings in the Presence of Mild Seismicity. Proceedings, 2(8), 432. https://doi.org/10.3390/ICEM18-05288





