Inverse Analysis for Estimating Temperature and Residual Stress Distributions in a Pipe from Outer Surface Temperature Measurement and Its Regularization ^†

Abstract

This paper presents an inverse analysis method for estimating the temperature and thermal residual stress distributions in the pipe from the temperature history measured on the outer surface. A regularization method was introduced. It is found from numerical simulations that the proposed inverse analysis method with regularization is useful for obtaining a reasonable estimate of the inner surface temperature and thermal stress.

1. Introduction

It was revealed that fluctuation of fluid temperature in a pipe may induce high cycle thermal fatigue in the pipe, which sometimes results in fracture of the pipe [1,2,3,4]. The information about the temperature and thermal residual stress distributions is important to prevent the high cycle thermal fatigue. It is, however, difficult to measure the temperature in the pipe directly. The monitoring of the temperature on accessible outer surface is promising to solve the problem. This paper presents an inverse analysis method for estimating the temperature and thermal stress distributions in the pipe from the temperature history measured on the outer surface. A regularization method is proposed for obtaining a reasonable solution.

2. Mathematical Structure of Temperature Distribution in a Thin Pipe

Consider a pipe subjected to thermal fluctuation on its inner surface. As an extreme the thickness of the pipe h is assumed to be small compared with the radius of the pipe. The governing equation of temperature distribution $\varphi (x,t)$ is expressed by the following equation of thermal conduction.

$$\frac{\partial \varphi (x,t)}{\partial t}=k\frac{{\partial }^2\varphi (x,t)}{\partial x^2}$$

(1)

Here x is the distance from the inner surface of the pipe, t is time and the k is the thermal diffusivity. Suppose that the inner surface temperature $\varphi (0,t)$ is given by a sinusoidal function of angular velocity $\omega$ as:

$$\varphi (0,t)=a\cos \omega t+b\sin \omega t$$

(2)

Taking account of the fact that the temperature is supposed to decay with x, we are interested in the following solution of Equation (1):

$$\varphi (x,t)=a{e}^{-x\sqrt{\frac{\omega }{2k}}}\cos \left(\omega t-x\sqrt{\frac{\omega }{2k}}\right)+b{e}^{-x\sqrt{\frac{\omega }{2k}}}\sin \left(\omega t-x\sqrt{\frac{\omega }{2k}}\right)$$

(3)

Then the temperature on the outer surface of the pipe $\varphi (h,t)$ is given as,

$$\varphi (h,t)=a{e}^{-h\sqrt{\frac{\omega }{2k}}}\cos \left(\omega t-h\sqrt{\frac{\omega }{2k}}\right)+b{e}^{-h\sqrt{\frac{\omega }{2k}}}\sin \left(\omega t-h\sqrt{\frac{\omega }{2k}}\right)$$

(4)

From Equations (2) and (4) it is seen that the amplitude of the outer surface temperature compared with that of the inner surface temperature is reduced by ratio R, and that the phase of the outer surface temperature is delayed by Δp compared to the inner surface temperature, and R and Δp are given as [5,6]:

$$R=e^{-h\sqrt{\frac{\omega }{2k}}}$$

(5)

$$\Delta p=h\sqrt{\frac{\omega }{2k}}$$

(6)

3. Inverse Method for Estimating Temperature and Thermal Stress Distributions

When the temperature on the outer surface $\varphi (h,t)$ is expressed by periodical function of time t with cycle time T, $\varphi (h,t)$ is expressed by the Fourier expansion as:

$$\varphi (h,t)=\frac{A_0}{2}+{\displaystyle \sum _{m=1}^{\infty }{A}_m\cos \left(\frac{2\pi m}{T}t\right)}+{\displaystyle \sum _{m=1}^{\infty }{B}_m\sin \left(\frac{2\pi m}{T}t\right)}$$

(7)

Based on the mathematical relationship between the temperature on the outer surface $\varphi (h,t)$ and that on the inner surface $\varphi (0,t)$ discussed in the foregoing section, the inner surface temperature history is estimated by amplifying $\varphi (h,t)$ by a ratio 1/R and also by advancing the phase by Δp:

$$\varphi (0,t)=\frac{A_0}{2}+{\displaystyle \sum _{m=1}^{\infty }\frac{A_m}{R_m}\cos \left(\frac{2\pi m}{T}t+\Delta p_m\right)}+{\displaystyle \sum _{m=1}^{\infty }\frac{B_m}{R_m}\sin \left(\frac{2\pi m}{T}t+\Delta p_m\right)}$$

(8)

Here the reduction ratio R_m and the phase lag Δp_m for the m-th term in the series are expressed as,

$$R_m=e^{-h\sqrt{\frac{\omega }{2k}}}=e^{-h\sqrt{\frac{\pi m}{kT}}}$$

(9)

$$\Delta p_m=h\sqrt{\frac{\omega }{2k}}=h\sqrt{\frac{\pi m}{kT}}$$

(10)

4. Regularization Method

The reduction factor R_m given by Equation (9) is very small for very high frequency component, or large value of m. Then high frequency fluctuation measured on the outer surface is exaggerated in the estimation of the inner surface temperature history. In the presence of measurement noise, incorrect high frequency components deteriorate the estimation. We introduce a regularization method to exclude the incorrect components. This limit is determined by considering the effect of noise to the coefficient of the Fourier coefficients. When the error in outer surface temperature measurement is of the order of δ, the expected amplitude of the Fourier coefficient is in the order of $\delta /\sqrt{6}$. Then regularization was conducted by ignoring the Fourier coefficient of the outer surface temperature, whose absolute value is smaller than this value.

5. Estimation of Thermal Stress Distribution

The total strain ${\epsilon }_0$ is composed of thermal strain ${\epsilon }_t$ and mechanical strain ${\epsilon }_m$:

$${\epsilon }_0={\epsilon }_t+{\epsilon }_m=\alpha \varphi +{\sigma }_t/E$$

(11)

Here E is Young’s modulus and ${\sigma }_t$ denotes thermal stress. The total strain is independent of x due to uniform deformation of the long pipe. Then the equilibrium of thermal stress gives rise to the following expression of the thermal stress.

$${\sigma }_t=\alpha \left(\frac{{\displaystyle {\int }_{x=0}^{x=h}\varphi dx}}{h}-\varphi \right)E$$

(12)

6. Numerical Simulations

Numerical simulations were made to examine the applicability of the proposed method. A pipe made of type 316 stainless steel is considered. The thermal diffusivity is $4.46\times {10}^6$ m²/s. Young’s modulus is 193 GPa. The thickness of the pipe h is 0.015 m, the cycle time T is 100 s. It is assumed that the inner surface temperature is given by superposing three waves, whose amplitude and cycle period are given in Table 1. As the error in the outer surface temperature measurement, 2 °C, 5 °C and 8 °C were employed. Artificial error was introduced using uniform random number.

Table 1. Amplitude and cycle period of three waves introduced.

Wave	1	2	3
Amplitude [°C]	100	50	30
Cycle Period [s]	20	50	5

Figure 1a–c show the inner surface temperature history by applying the estimation method without regularization for the measurement error of 2 °C, 5 °C and 8 °C, respectively. It is seen that the estimated inner surface temperature (blue line) is fluctuated around the real one (red line). As the noise level is increased high frequency components give rise to big fluctuation in the estimated inner surface temperature history. The fluctuation is pronounced for large measurement error.

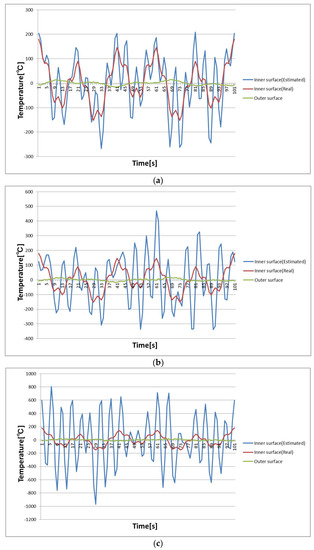
Figure 1. Estimated temperature variation on inner surface without regulation. (a) Observation noise of 2 °C; (b) Observation noise of 5 °C; (c) Observation noise of 8 °C.

Figure 2a–c show the inner surface temperature history by applying the estimation method with regularization for the measurement error of 2 °C, 5 °C and 8 °C, respectively. It is found that a reasonable estimation is made by applying the regularization method even in the existence of considerable observation error, although the information about the very high frequency component is lost.

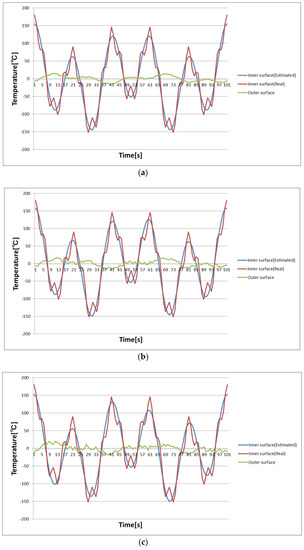
Figure 2. Estimated temperature variation on inner surface with regulation. (a) Observation noise of 2 °C; (b) Observation noise of 2 °C; (c) Observation noise of 8 °C.

Using the temperature history the estimation of the thermal stress in the pipe was made. As an example the thermal stress at t = 5 s for the three waves examined in the foregoing are shown in Figure 3. Thermal fatigue life can be evaluated using the estimated thermal stress and counting the number of cycles.

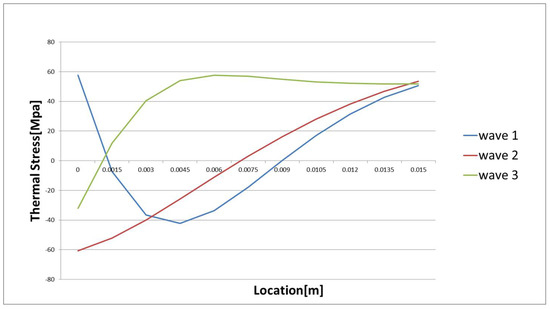
Figure 3. Thermal stress distribution at t = 5 s.

7. Conclusions

An inverse analysis method was presented for estimating the temperature and thermal stress distributions in the pipe from the temperature history measured on the outer surface. Regularization method was introduced. It was found that the proposed inverse analysis method with regularization was useful for obtaining a reasonable estimate of the inner surface temperature and thermal stress.