Abstract
The objective of this work is to build a quantitative relationship between the fiber break as source of Acoustic Emission (AE) and the detected signal by unravelling the effect of each stage of the AE acquisition chain. For this purpose, an AE modelling is carried out using the Finite Element Method and then the simulation is compared to experimental results of Single Fiber Fragmentation Test (SFFT). The SFFT is used in order to produce preferential fiber break. It is carried out on specimens made from a long carbon fiber embedded in epoxy/amine matrix. Two different types of sensor are used in order to gather information on a wider frequency bandwidth. For the modeling part, the entire geometry of the specimen is modelled using Finite Element Method. There is a good agreement between experiment and modeling results.
1. Introduction
The Acoustic Emission technique is widely used to detect failures in composite materials. This non-destructive technique detects real-time failure occurring during mechanical loading. When a microscopic crack occurs, it releases an elastic wave that propagates to the surface and that can be detected by suitable sensors. This wave is recorded by the acquisition system and is further analyzed.
In polymer matrix composites, three different failure modes are mostly identified: fiber breakage, matrix cracking, and interfacial debonding. Because of the overlapping of these different failure modes, signal identification and classification through AE is not an easy task. Furthermore, many complexities are present in AE techniques. In fact, the wave originating from the AE source is altered during propagation, by the propagation medium and eventually by the recording system. All these transformations make the interpretation of the signals very difficult. It is important to discern the role of the source from the effect of the transformations due to the propagation medium and the recording system on the measured signal. Therefore, the aim of this work is to build a quantitative relationship between the fiber break as source of AE and the detected signal by unravelling the effect of each stage of the acquisition chain, namely the detection system and the propagation medium [1,2,3]. For this purpose, an AE modelling is carried out using the Finite Element Method (FEM) code ABAQUS®, and then the simulation is compared to experimental results of Single Fiber Fragmentation Test (SFFT). From an experimental point of view, the SFFT is used in order to produce preferential fiber break. For the modeling part, the entire geometry of the specimen is modelled, and a dynamic calculation is performed. The model is then used to understand and to quantify the effects of the propagation medium and of the sensor on the signal waveform.
2. Materials and Methods
2.1. Experimental Setup
The specimen is made of a single long carbon fiber T700 embedded in epoxy/amine matrix: 1,4-Butanedioldiglycidyl ether (DGEBD)/4,4′-Methylenebis(2-methylcyclohexylamine) (3DCM). The dimension of the specimen is shown in Figure 1.
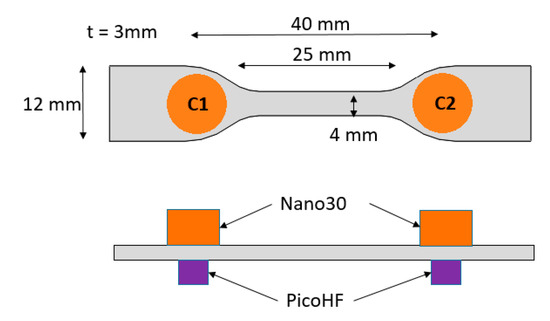
Figure 1.
Dimension of specimen and sensors placement.
Concerning the AE system, two types of piezoelectric transducers were used as shown in Figure 1, namely the nano30 and the picoHF from Euro Physical Acoustics. The distance between each couple of sensors is 40 mm. These sensors detect signals propagating on the surface of the specimen, and then recorded using a Physical Acoustic PCI-2 system at an acquisition rate of 5 MS/s.
The SFFT is a tensile test applied on single fiber composite in axial direction, in order to create fiber breakage. Usually the debonding occurs at the same time of the fiber breaks, but in our case, because of a high interfacial strength, debonding does not occur. The SFFT is carried out using the tensile test machine (type: MTS, capacity 5 kN), at room temperature and with a deformation rate of 0.5 mm/min. The post-treatment of the experimental results is based on the calculation of descriptors as defined in [4,5] and time frequency according to smoothed pseudo Vgner-Ville distribution. In our work, we calculated descriptors as signal amplitude, energy, frequency centroid (FC), peak frequency (PF) and partial powers (PP).
2.2. Numerical Setup
The single fiber fragmentation is modeled using FEM by means of Abaqus® software (6.14-5) with dynamic calculation. We modeled the entire geometry of the specimen: the boundary conditions are shown in Figure 2. The geometry is meshed using tetrahedral elements (type = C3D4), the element size varies between 0.01 mm for fiber and 0.2 mm elsewhere.
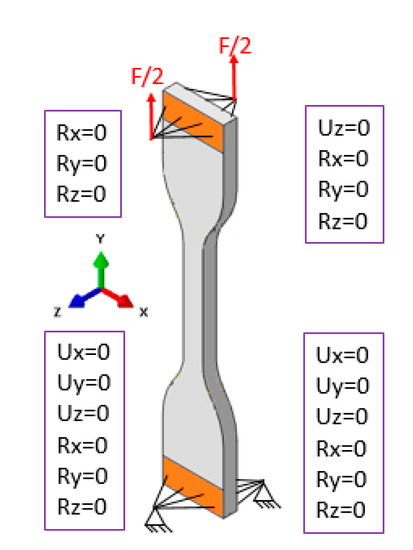
Figure 2.
Scheme of the numerical specimen with the boundary conditions.
The main properties of the material are shown in Table 1. The viscoelasticity of the matrix is taken into account by the Rayleigh parameters (alpha = 50 and beta = 3 × 10−11). The fiber breakage is modelled by separating the nodes forming fracture faces and creating wave. The numerical signals are collected on the specimen surface.

Table 1.
mechanical properties of materials.
The sensor is taken into account by its transfer function shown in Figure 3, which is experimentally determined by the reciprocity method [6].
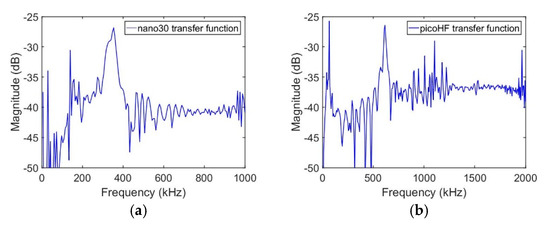
Figure 3.
Transfer function of (a) nano30 and (b) picoHF, determined by reciprocity method.
3. Results and Discussion
3.1. Experimental Results
3.1.1. Localization of AE Sources
After waveform acquisition during SFFT, the signals source position was determined. A good agreement has been found between the number of localized sources detected by AE and fiber breakage observed by means of transmission optical microscope (Figure 4).
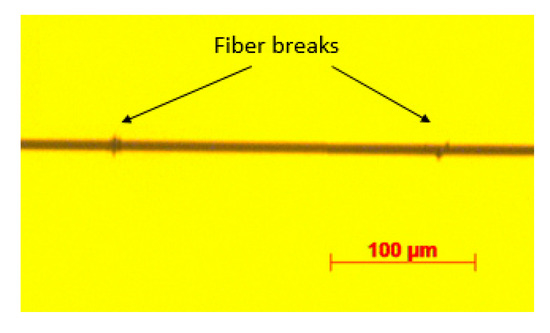
Figure 4.
Fiber breaks as observed by optical microscopy.
Therefore, in our tests, all located sources are assigned to fiber breaks. In Figure 5, the cumulative number of localized signals are presented for the types of sensors used in our tests. The sensors have localized exactly the same sources. So, both are suitable for this test.
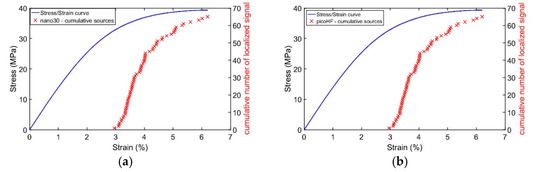
Figure 5.
Cumulative localized signal during SFFT: (a) sources located by nano30; (b) by picoHF.
3.1.2. Effect of Distance between Source and Sensor on AE Results
The calculation of descriptors shows a clear dependency of distance between the source and the sensor on the results. Table 2 shows a summary of some descriptors: we compare descriptors mean values of the sources near and far for sensors, for two different tests (AF02 and AF03) and two types of sensors (nano30 and picoHF). Figure 6 shows the evolution of temporal and frequency descriptors with the distance source/sensor, for two different tests and with nano30 sensor. The amplitude, calculate in dB, varies linearly with distance and it loses 25 dB between the nearest and the furthest fiber break. The energy decreases drastically with distance. The frequency also centroid decreases linearly from 300 kHz to 140 kHz and the peak frequency takes two main values, the higher is equivalent to the resonant frequency of the sensor.

Table 2.
Descriptors calculated for two SFFT.
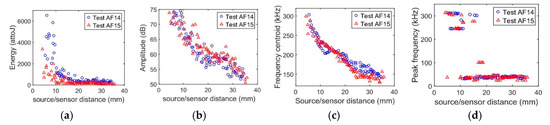
Figure 6.
Temporal descriptors vs. source/sensor distance: (a) energy in attoJ, (b) amplitude in dB, (c) frequency centroid in kHz and (d) peak frequency in kHz.
The Figure 8 shows the time-frequency maps assigned to three fiber breaks for three positions on the specimen as shows in Figure 7. The sensor used here is nano30. For fiber breaks near to the sensors (Figure 8a) show a content of high frequency that progressively disappears when the sources become further.
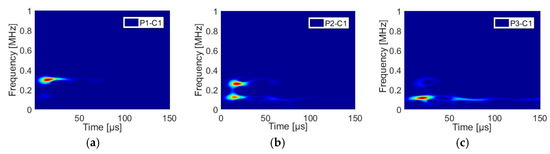
Figure 8.
Figure 8. Time-frequency results calculated using smoothed pseudo Vigner-Ville distribution for 3 source positions for signals recorded on C1: (a) P1 position, (b) P2 position and (c) P3 position
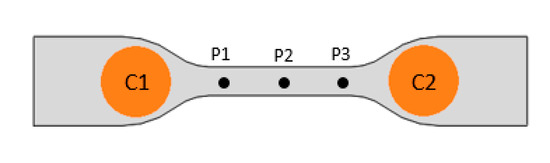
Figure 7.
Position of the three fiber breaks in the specimen.
The frequency content of signals varies significantly with distance source/sensor. Some signals have only low frequency content. Due to this dependency, these results cannot allow to define an acoustic signature of fiber breakage. In some works (reference), the authors save only signal detected by the nearest sensor to obtain descriptors relatively stable in relation to position of sources.
3.1.3. Effect of Sensor Type: Comparison Results of PicoHF with Results of Nano30
The nano30 is very sensitive around 300 kHz and does not detect high frequency as from 500 kHz. The picoHF is very responsive around 500 kHz and detects high frequencies. Therefore, when sensors detect signals from the same source, they do not respond in the same way. In Figure 9, we compare two signals in the temporal and frequency domain, stemmed from the same source and detected by nano30 and picoHF sensors. These two sensors are equidistant from the source. With a coefficient of correlation of 25% in the frequency domain, it is clear that those different sensors do not detect the same information; especially beyond 200 kHz. Therefore, they give certainly complementary information about the source.
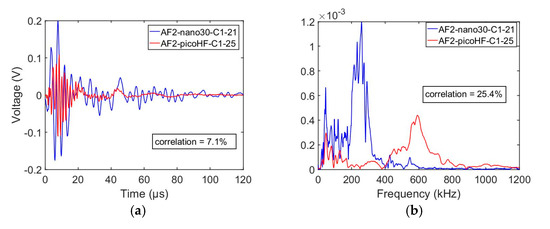
Figure 9.
Temporal signals (a) and frequency spectra (b) for two types of sensors.
3.2. Results of the Numerical Model
In this part, three fiber breaks are modeled for three different positions as shown in the Figure 7. Each break is simulated for 150 µs, which is sufficient to attenuate the signal.
3.2.1. Numerical Results without and with Sensor
We have simulated fiber fragmentation for 2 cases: punctual non-resonant sensor where the out-of-plane velocity is collected on one single point and cylindrical sensor taking into account its transfer function (nano30), where the velocity is collected on the surface contact. Then the average velocity is convoluted by the transfer function of the sensor.
In Figure 10, we compared the velocity on C1 sensor for these three cases. High frequencies dominate for punctual sensor. For cylindrical sensor, those high frequencies are lost. We can see also the effect of nano30 sensor by amplifying frequencies around 300 kHz.
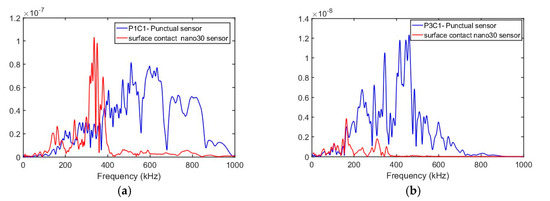
Figure 10.
Comparison between simulated punctual sensors, surface contact sensors. (a) Signals of simulated fiber break at P1 position at C1 sensor; (b) at P3 position at C1 sensor.
3.2.2. Comparison Numerical and Experimental Results
In order to compare experimental and numerical results, we perform a calculation in time-frequency domain. The maps of Figure 11 present the numerical results for the three points shown in Figure 7 taking into account the nano30 sensor. The velocity is calculated on C1. A good agreement is found between the experimental results show in Figure 8 and numerical results. The evolution of the signals is very similar.
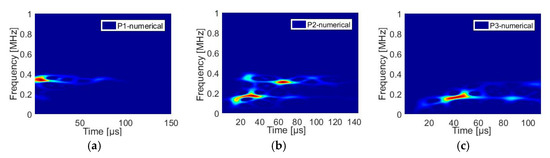
Figure 11.
Numerical results: time frequency calculated with smoothed pseudo Vigner-Ville distribution for three source positions: (a) P1 position, (b) P2 position and (c) P3 position
4. Conclusions
The aim of this work is to define an acoustic signature of fiber breakage in composite materials. From an experimental point of view, the calculation of classical descriptors does not give steady characteristics of this mode of failure. They are very dependent on the distance between the AE source and sensor. Their dependency is due to the damping characteristic of material and the geometry. The use of second type of sensor allows gathering more information about the failure mode. These results cannot be generalized on other cases because they depend on the geometry, the material, the sensor and the distance between sensors.
The modeling is an efficient tool that allows us to better understand the influence of different parameters on the results, such as the geometry, the location of source and the sensor effect. So far, the modeling helps us to understand the effect of sensors.
References
- Giordano, M.; Cndelli, L.; Nicolais, L. Acoustic Emission wave propagation in viscoelastic plate. Compos. Sci. Technol. 1999, 59, 1735–1743. [Google Scholar] [CrossRef]
- Sause, M.G.; Richler, S. Finite element modelling of cracks as acoustic emission sources. J. Nondestruct. Eval. 2015, 34, 4. [Google Scholar] [CrossRef]
- Le Gall, T.; Godin, N.; Monnier, T.; Fusco, C.; Hamam, Z. Acoustic Emission modeling from the source to the detected signal: Model validation and identification of relevant descriptors. J. Acoust. Emiss. 2017, 34, S59–S64. [Google Scholar]
- Morizet, N.; Godin, N.; Tang, J.; Maillet, E.; Fregonese, M.; Normand, B. Classification of acoustic emission signals using wavelets and Random Forests: Application to localized corrosion. Mech. Syst. Signal Process. 2016, 70, 1026–1037. [Google Scholar] [CrossRef]
- Godin, N.; Reynaud, P.; Fantozzi, G. Acoustic Emission and Durability of Composite Materials; John Wiley & Sons: Hoboken, NJ, USA, 2018. [Google Scholar]
- Monnier, T.; Seydou, D.; Godin, N.; Zhang, F. Primary calibration of acoustic emission sensors by the method of reciprocity, theoretical and experimental considerations. J. Acoust. Emiss. 2012, 30, 152–166. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).