Abstract
To characterize the mechanical behaviour at high temperature close to the melting point, a tensile test machine has been developed through resistive heating by Joule effect. A closed chamber is designed to control the working environment. By the two windows in the chamber, the temperature and displacement fields can be measured directly. For the machine, both temperature and tensile force can be controlled by the proportional-integral-derivative controller. In this paper, the main features of the machine’s design and development will be discussed, with a specific section dedicated to the optimization of the specimens’ shape, which is of utmost importance in the context of Joule heating.
1. Introduction
The quality of numerical simulations of processes involving metal solidification highly depends on how good the characterization of the mechanical behaviour is at high temperature, close to the melting point. This is notably true for simulation processes like casting, welding or additive manufacturing when predicting defects initiated at high temperature, such as porosities, hot tearing and distortions [1,2]. In order to proceed with such characterization, the thermal-mechanical physical simulation system of the well-known Gleeble machine is usually adopted [3]. This machine can heat the specimen through a resistance or induction heat system at a high heating rate. However, the geometry of specimens and the accessible measurement highly depends on the Gleeble machine. For more information and to apply a more flexible geometry, inhouse “Gleeble” machines are designed for different applications with low cost [4,5].
Based on the first generation of resistive heating tensile test machine “Taboo” [5], the machine “Dedimet” is designed with controlled working environment, thanks to a closed chamber. Like a “Gleeble”, the developed set-up can be used to physically simulate thermomechanical routes encountered during manufacturing of metals, such as heating to get close to the melting point, cooling after solidification and reheating to proceed with heat treatment. For the heating route with uniaxial tension and relaxation loading cycle at small strain and low strain rate, the material constitutive law can be determined for welding or additive manufacturing. Applying such thermomechanical history to a sample and studying the consequences in terms of microstructure evolution is obviously extremely interesting to optimize manufacturing processes.
After a quick overview of the machine, we will discuss the heating system principle, the proportional-integral-derivative (PID) controller for temperature and force, and the optimization of specimens’ shape.
2. Machine Overview
The design work started around an Adamel electromechanical 30 kN tensile test machine housing with the addition of a vacuum chamber to reach, at the lowest, a few mbar. This one is equipped with several connectors: arrival of inert gas, signal measurement outlets (temperature, load, displacement…), electrodes for resistive heating, but also inductor connections for future studies. The whole design is shown on Figure 1.
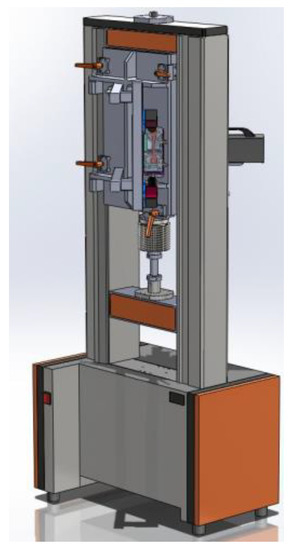
Figure 1.
Machine overview.
The machine movement is ensured by its electrical motor, with a 1000 pulses per revolution encoder and a Keyence laser system enabling accurate displacement (resolution < 0.5 µm). The load measurement is performed by a HBM 25 kN sensor while the temperature is measured through several methods as described in part 5. Temperature measurement, including two infrared measurements thanks to the ZnSe window. Strain field measurement can also be performed on the front face through a standard glass window.
Finally, special clamps were designed to apply electrical current to the sample while the rest of the mechanical assembly remained safe thanks to insulating ceramics. By the way, Figure 2 highlights the chamber with all the previously listed elements.
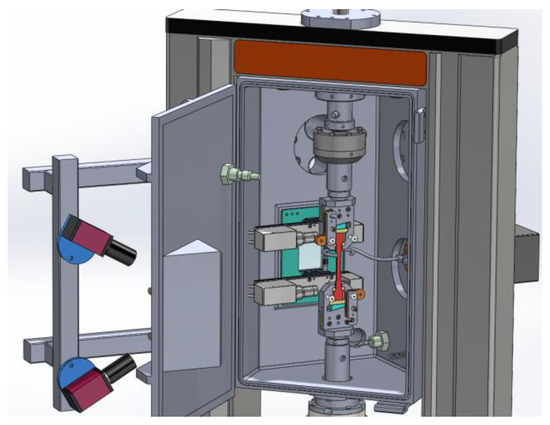
Figure 2.
Focus on the chamber.
3. System of Temperature Control
Similar to the well-known Gleeble machine, the machine discussed here is designed to heat the specimen as high as 1300–1400 °C in short heating times in the closed chamber. In the context of our work, the specimen shown in Figure 3 is heated by Joule effect within a controlled environment. During the test, grips are maintained at low temperature thanks to the use of cold water circulating inside the grips parts. For the electrical boundary conditions, zero voltage is imposed on one surface and current density is applied on the other surface.

Figure 3.
Specimen.
3.1. Heating by Joule effect
By Ohm’s law, the current density J can be expressed by
where is the electric conductivity, is the electrical field expressed by , where is the electric potential.
If we consider the corresponding volume power as = = in the analysis domain Ω, the potential and temperature distribution in Ω is governed by considering electrical charge and energy conservation, following partial differential equations:
In the above equation, ρ is the material density, is the thermal conductivity and the specific heat. More details can be found in [3,6].
3.2. Proportional–Integral–Derivative Controller (PID) for Temperature Regulation
In order to maintain the useful zone temperature around a desired value, the Proportional–Integral–Derivative (PID) controller is used to control one accessible point. In each time step i, the value of current density is determined as follows, according to the temperature error function.
where , and are the associated constants for proportional, integral and derivative terms, respectively. For the variables, i is the current time step and j is the index of the selected time n steps for the integral item. The error is considered by the temperature difference between the calculated and prescribed values:
4. Optimization of Specimen Design
In order to easily access the temperature and displacement fields, flat specimens with rectangular cross section are selected. The specimen is heated by Joule effect reacting as an electrical resistor, and the temperature along the center line depends on the material electrical resistivity and the specimen shape to be optimized. In the current design, the specimen is heated to reach temperatures as high as 1.300–1.400 °C in short heating times under maximum current of 400 A. The optimization was achieved through the finite element software FORGE®, combining its electrical and thermal solvers as given in Equation (2). Simulations were realized to optimize the thickness of each section, the shape of the transition zone and the length of the central working zone in order to have a quasi-uniform high temperature, while maintaining temperature in the grips to an acceptable low level (Figure 4a,b). It is worth mentioning that only a small plateau is obtained around the center of the working zone, due to potential gradient in Equation (2). However, this doesn’t influence the material characterization due to adopted temperature field for the inverse analysis. Finally, the thickness 4-4-2 with a working length of 56 mm is adopted to maintain a relative large plateau in the center zone and low temperature in the grips, as shown in Figure 4c.
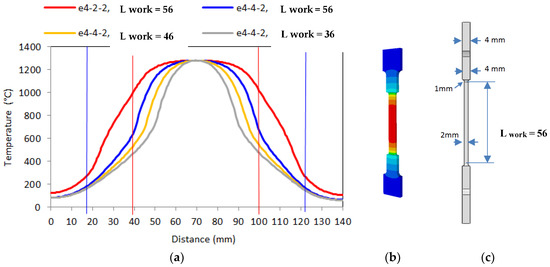
Figure 4.
Geometry optimization: (a) Temperature profile along the specimen center line; (b) Temperature distribution in the specimen; (c) Optimized geometry.
5. Temperature Measurement
Temperature is measured by both contact method and non-contact method. In the contact method, K type thermocouples are welded on the sample to measure the temperature at points of interest. The temperature control is then based on the feedback of one of those using the PID regulation referring to Equation (3) (usually the one welded at the center of the specimen). In the non-contact method, a bichromatic pyrometer is used to measure the temperature at a spot of interest with a diameter almost equivalent to that of the specimen while a bichromatic camera called Q-Pyrocam (developed by IMS-Chips Company—Stuttgart, Germany) is used to measure the temperature field of the whole sample. The advantage of such local or field bichromatic temperature measurement is that no emissivity measurement is required.
In the temperature field measurement, the Q-Pyrocam is placed in the line centrally normal to the sample and the measurement is taken after its calibration in situ. The image data of temperature field is then analyzed with MatLAB as shown in Figure 5, representing the temperature field of a stainless steel 304 sample.
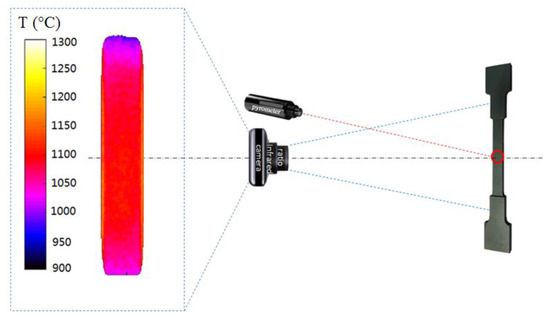
Figure 5.
Temperature field measurement and schematic diagram on the non-contact measurement
6. Monitoring Design and Experimental Tests
Other than Q-Pyrocam data, the entire system is monitored by a LabVIEW application illustrated in Figure 6. This software allows us to drive the actuators, but also to record data from all sensors parallelizing and clocking each task with software, mechanical and electrical securities.
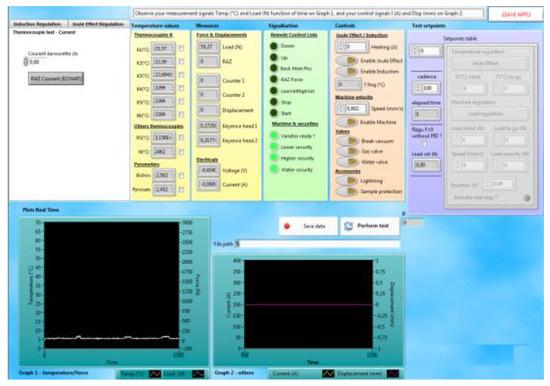
Figure 6.
LabVIEW user interface.
Specimens were submitted to thermo mechanical paths representative of material using conditions such as constant heating rate from 20 °C to 1200 °C thanks to thermal PID loop regulation accommodating thermal dilatation with “zero” load loop regulation. The inverse loading path with constant cooling rate has also been achieved to reach stresses between 600 and 1000 MPa. The result of this kind of experiments is shown in the graph of Figure 7.
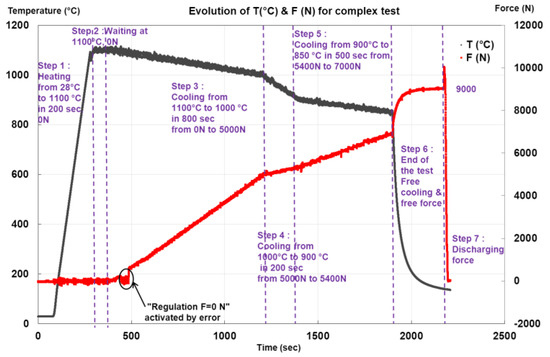
Figure 7.
Complex test with load and temperature PID monitoring.
7. Discussions and Conclusions
In conclusion, we thus explored in this paper a second-generation high temperature tensile test machine, which was developed in-house by a highly skilled team in CEMEF facilities, inducing lower costs compared to the purchase of a “Geeble” machine.
Using Forge software, we were able to optimize the specimen design and establish thermo mechanical simulation settings. These ones were deployed in LabVIEW, the software selected to drive the machine with its built-in PID toolkit, to be used for experimental campaigns.
With regard to thermal measurements, outstanding technological choices were made in order to overcome the material emissivity variations during testing. As temperature control, load can be controlled to compensate for the material expansion or contraction.
Finally, we keep working hard to achieve a perfect synchronization between displacement field measurements and thermal field measurements in order to best characterize how materials behave from a thermo mechanical perspective at high temperatures in the context of processes such as additive manufacturing.
References
- Harrison, N.J.; Todd, I.; Mumtaz, K. Reduction of micro-cracking in nickel superalloys processed by Selective Laser Melting: A fundamental alloy design approach. Acta Mater. 2015, 94, 59–68. [Google Scholar] [CrossRef]
- Koshikawa, T.; Bellet, M.; Gandin, C.A.; Yamamura, H.; Bobadilla, M. Study of hot tearing during steel solidification through ingot punching test and its numerical simulation. Metall. Mater. Trans. A 2016, 47, 4053–4067. [Google Scholar] [CrossRef]
- Zhang, C.; Bellet, M.; Bobadilla, M.; Shen, H.; Liu, B. A Coupled Electrical–Thermal–Mechanical Modeling of Gleeble Tensile Tests for Ultra-High-Strength (UHS) Steel at a High Temperature. Metall. Mater. Trans. A 2010, 41, 2304–2317. [Google Scholar] [CrossRef]
- Maisonnettea, D.; Sueryb, M.; Nelias, D.; Chaudet, P.; Epicier, T. Effects of heat treatments on the microstructure and mechanical properties of a 6061 aluminium alloy. Mater. Sci. Eng. A 2011, 528, 2718–2724. [Google Scholar] [CrossRef]
- Pradille, C.; Bellet, M.; Chastel, Y. A Laser Speckle Method for Measuring Displacement Field. Application to Resistance Heating Tensile Test on Steel. Appl. Mech. Mater. 2010, 24–25, 135–140. [Google Scholar] [CrossRef]
- Pradille, C. Vers une Meilleure Compréhension et Caractérisation du Comportement des Aciers à très Haute Température. Ph.D. Thesis, École Nationale Supérieure des Mines de Paris, Paris, France, 2011. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).