Abstract
Selecting appropriate skis remains a difficult task for many customers due to the lack of information provided on the bending and torsional stiffnesses of these products. This work investigates how these mechanical properties influence the on-snow ski performance and how an individual skier profile is related to its preferred mechanical properties. To do so, twelve skis were manufactured to exhibit large variations in stiffnesses. Twenty-three skiers provided on-snow feedback and skier profiles through a questionnaire. Simple and multivariable linear correlation analyses were carried out between the skier profile data, their evaluations of the skis and the stiffnesses of the skis. Strong relationships were found between the properties of the skis and some performance criteria, and between the profile of the skiers and the properties of their favourite skis. With further testing, these relationships could be used to design personalized recommendation tools or to guide the design of custom skis.
1. Introduction
Every year, manufacturers introduce hundreds of new ski models to the market. Consumers, either online or in shops, can perceive differences in cosmetics, in geometry, in mass and in price. However, no information is provided on the bending and torsional stiffnesses. This lack of information about the stiffnesses makes ski selection difficult as these properties greatly influence the on-snow performance of a ski [1]. This is why many customers often rely exclusively on the elusive demo days to guide their final decision.
To help the customer select appropriate ski, various tools can be envisioned. Previous work, studied the preferred bending and torsional stiffnesses of giant slalom [2] and slalom skis [3,4]. Their analysis often included two variables correlation (i.e., Pearson or Spearman) between ski stiffnesses and performance criteria following on-snow tests, either using quantitative (e.g., running time) or subjective criteria (e.g., survey). All these studies allude to the difficulty of building or selecting skis with large and independent variation in stiffnesses. They ultimately used between three and four different pair of skis in their on-snow tests. For slalom skis, both [3,4] converged to the same preferred bending and torsional stiffnesses. These promising results, obtained with expert male skiers on racing skis, remains however difficult to relate to for skiers with different profiles, styles and abilities.
The work presented in this paper uses twelves custom-built all-mountains skis tested by 23 skiers, men and women of various backgrounds, to investigate ski performance and user preferences. The twelves skis exhibit large variations in stiffnesses that are representative of the variation found in commercial products. Skier profiles and on-snow feedback are used to develop tools that could help customers select appropriate products. More specifically, this paper presents an algorithm to predict the on-snow performance given the mechanical properties of the skis and a ski recommendation algorithm based on the individual skier profile. In both cases, multivariable analysis are used to capture the complex relationship between the mechanical properties, the on-snow performance and the skier profiles, and the results are compared to two variables correlations.
2. Materials and Method
The following sections describe the manufacturing process of the skis, presents the questionnaire, the test procedure and the participants.
2.1. Ski Design
For controlling test parameters, an all-mountain ski from Xalibu was modified 12 ways to have different bending and torsional stiffness while maintaining the same geometry. The ski is 94 mm wide at the waist for a balance of lift in the powder and edge grip on groomed snow. The chosen geometry gives the ski a natural sidecut radius of 18 m. The ski measures 171 cm and has tip-rocker for ease of turn initiation on harder snow.
The stiffnesses are varied around the initial Xalibu’s design. Figure 1a illustrates the bending and torsional stiffness distributions of this ski as measured by the apparatus described by [5]. Eleven other skis pairs were designed by varying the bending and torsional stiffness by approximately ±100 N m2. A software design tool was developed to estimate stiffness distributions in bending and torsion at any point given the section geometry and the materials used. This tool was used to vary the bending and torsional stiffnesses somewhat independently while minimizing the mass variation and respecting the laminate availability of the manufacturer (Utopie MFG, Rimouski, QC, Canada). Figure 1b shows the measured and theoretical distribution of the twelve ski pairs as a function of their maximum bending and torsional stiffness.
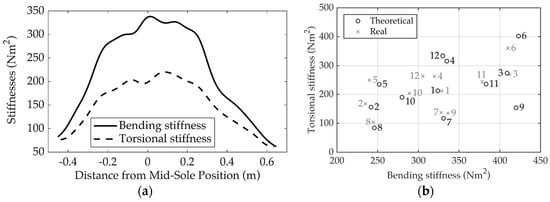
Figure 1.
(a) Distribution of ski bending and torsional stiffness; (b) Maximum bending and torsional stiffness of the twelves pairs of skis.
This validation demonstrates that an error occurred during the fabrication of ski number 9. The wrong core was used by the manufacturer and the bending stiffness is thus lower than expected. Otherwise, the predictions correspond rather well to the stiffness measured. As a result of variations in stiffnesses, the twelve ski pairs also have variations in mass (mean = 1.57 kg, kg) and camber (mean = 8.41 mm, mm). Although small compared to the variation of the stiffnesses, these variation of mass and camber have also been taken into account in the analysis.
2.2. Questionnaire
The questionnaire consists of two sections. The first section, the skier profile, collects skier weight, height, skill level, and preferences in terms of skiing style and desired performance. The question style is deliberately varied (text, checkboxes and numbering) to keep the tester attentive. The second section collects the impression of skiers on each ski according to seven performance criteria which are edge grip, ease in initiating a turn, energy of restitution, versatility, stability, performance in short radius, performance in long radius and overall impression. To these criteria is added three summary questions to elicit beliefs about which conditions are best suited to the ski. These environmental criteria are the speed (slow to fast), the style (finesse to force) and the turning radius (short to long). A scale between 1 and 7 was chosen to make it possible to identify more subtle differences between the skis. The criteria were explained to the participant prior to the on-snow test.
2.3. Procedure
For the tests, the skis were subdivided into three groups. In the first group, the skis distinguished themselves by their differences in bending (i.e., 2-3-10-11). In the second group, the skis distinguished themselves by their differences in torsion (i.e., 1-4-7-12). In the third group, the skis varied both in bending and torsion (i.e., 5-6-8-9). The participants were not aware of the differences between the groups, but this division makes it possible to better feel the different stiffness properties on-snow. The skiers were invited to try one group at a time and to perform two runs with each pair of skis. Skiers had to try at least one group of skis to participate in the study. Each skier had a run with a GPS to record the average speed of the run as well as the maximum speed reached.
During the three test days, the average temperature was 10 °C and the snow was representative of spring conditions; firm groomer in the morning that became progressively softer, with small moguls, as the heat warms up the snow. The trails used were north facing to limit their variation during the day. They had a vertical drop of 320 m with a slope around 25°.
The skis were mounted with rental bindings from Tyrolia at the recommended mounting point. Similar models were used although cosmetically different. Users provided their own boots for testing and the binding were adjusted to their preferred DIN setting.
2.4. Participants
A total of 23 advanced or expert participants were recruited. The participants included 20 men and 3 women. They were, on average, 30 years old (SD = 10), 1.76 meter tall (SD = 0.08), 75.7 kg (SD = 12.6) and they mostly like high speed skiing ( km/h, SD = 9). As the participants did not try the full twelve pairs of skis, it is necessary to validate the homogeneity of the groups. The homogeneity guarantee that all skis have been tried by similar participants and thus that the differences obtained between the skis are not caused by the difference between the participants. Homogeneity is validated using the information of the skier’s profile. The two-population homogeneity test was applied to each ski pair by comparing the skier group having tested the pair with those who have not tried the pair. The significance threshold was chosen at p = 0.05. The groups are homogeneous when all calculated p-values are greater than 0.05. Of the 216 p-values, 4% are less than 0.05. Given the small size of the group, this imperfection in homogeneity is tolerated.
3. Results and Discussion
The results of the on-snow tests were used to answer the two questions of interest in this study: can we predict the performance of alpine skis given its mechanical properties and can we predict a skier’s favorite ski (i.e., mechanical properties) given its skier’s profile. For these two questions, analyzes in two dimensions were compared to the more complete relationship found in N dimensions to validate the hypothesis that better predictions can be obtained through multivariate relationships.
3.1. Prediction of Performance
3.1.1. 2D Analysis
The Pearson coefficient denoted is used for 2D analysis. Of the eight performance criteria, three have significant relationships (r > 0.58, p < 0.05) with the properties of the skis. The edge grip is negatively correlated with the camber (r = −0.59, p = 0.04). The ease of initiation of a turn is negatively correlated with ski mass (r = −0.72, p = 0.01). Finally, versatility is negatively correlated with ski maximum torsional stiffness (r = −0.62, p = 0.03) and with ski mass (r = −0.62, p = 0.03). All of the relationships found intuitively make sense. Indeed, more camber will increase the pressure at the tips and favour edge grip. Lower mass will encourage easy pivoting of the skis during the initiation, and easier steering of the skis for various turn shapes. The versatility could also be encouraged by a lower torsional stiffness, which favour an easy release of the ski edge at any point during the turn.
As for the three indicators of the best environment for each ski (i.e., speed, style and radius) two of them correlated with ski properties. The speed is positively correlated with ski mass (r = 0.69, p = 0.01) and the style is positively correlated with maximum torsional stiffness (r = 0.62, p = 0.03).
3.1.2. N-D Analysis
Although there are significant two-dimensional relationships, in order to obtain better performance predictions, N-dimensional relations are also computed with the use of the coefficient of determination . As various number of dimensions could be used, all possible combinations between two and four dimensions are generated. The optimum combination is selected by comparing the adjusted R-Squared (), which account for the different dimensions. Also, it is necessary to know the threshold of significance of the coefficient . This threshold is dependent on the number of data in the problem, the number of dimensions, the probability α of wrongly rejecting the null hypothesis and the probability β of wrongly accepting the null hypothesis. The coefficients α and β are respectively defined at 0.05 and 0.1.
Of the eight performance criteria, only three significantly correlated with few ski properties. On the three environmental criteria, one significantly correlated with the ski properties. The results are shown in the Table 1. For example, the ease in initiating a turn is predicted from the torsional stiffness and the ski mass with an of 0.61. According to the adjusted, these relationships are stronger than the 2D found previously. Once the regression variables are known, Bayesian linear regression is used to identify the relationships. The linear regression coefficients are shown in Table 1.

Table 1.
Linear regression coefficient for each significant prediction.
In this case, the torsional stiffness is as detrimental to short-radius performance as to long-radius performance, but helps in the initial phase of the turn. It might also suggest that there is an optimum trade-off between torsional stiffness and turn initiation, for a given turn radius.
The size of the coefficients must be analysed with knowledge of the range of variation of each of these variables. In this study, the bending stiffness varied by 175 N m2, the torsional stiffness varied by 256 Nm2, the mass varied by 0.38 kg and the camber varied by 5 mm. To understand the importance of each variable, the influence of a variation of 10% of their range is studied on each performance criterion using the coefficient in Table 1. For example, the ease of turn initiation increases by 0.13 for a 10% increase in maximum torsional stiffness and decreases by 0.25 for a 10% increase in mass. Therefore, the mass of the ski is more important than the maximum torsional stiffness to predict the ease of initiation of a turn. Following the same analysis, the torsional stiffness is most important for the versatility criteria in spite of its smallest coefficient. Finally, short-radius performance and radius of turn are both more sensitive to variations in camber.
3.2. Recommandation
The second phase of this study involves relating the skier’s profile to the properties of the preferred ski for each skier. Again, this analysis begins with the calculation of the Pearson correlation coefficients to discover two-dimensional relationships and continues with multivariate analysis.
3.2.1. 2D Analysis
All the properties of the preferred skis are correlated with some information about the skier profile. The maximum preferred bending stiffness is positively correlated with the number of ski days (, ) and the forgiveness (, ) and negatively correlated with the versatility (, ). The maximum preferred torsional stiffness is correlated negatively with the preference for glades (, ) and versatility (, ). The preferred mass is positively correlated with the preference for stability (, ) and negatively correlated with the hardness of snow (, ), the preference for trails (, ) and versatility (, ). The preferred camber is positively correlated with the length of current skis (, ), the claimed speed (, ), the preference for backcountry (, ) and stability (, ) and is negatively correlated with the preference for forgiveness (, ).
3.2.2. N-D Analysis
Multivariate analysis was used to account for complex correlations between the preferred ski properties and the skier profile which are not captured with pair-wise analyses. The N-dimensional analysis of this problem is longer to process than the previous one due to the large number of possible parameters combinations of the skier profile. Not knowing whether the optimal solution is 2-dimensional or 29-dimensional, there are over 268 million possible combinations. To reduce the number of combinations to be tested, only combinations where all terms are independent are retained.
The results are significant for all the mechanical properties of the preferred skis, but are optimal in an adjusted R-squared sense with different combination of parameters from the skier profile. For example, the preferred bending stiffness is evaluated with 12 parameters for an of 0.96. The linear regression coefficients from a Bayesian linear regression are shown in Table 2 with the p-values corresponding to theses coefficients. When there is no value in the cell, this term is not part of the optimal equation to predict the preferred property. The coefficient in the table have different units depending on the variable. Skier mass and run speed correspond to a variation of one unit of normalized mass or speed, while the variables man, trails, backcountry, mogul, border and glade can only take the values 0 or 1 depending on whether or not it matches the skier’s profile. The turning radius can take a value between 1 (short) and 3 (long). The density of the snow can take a value between 1 (deep powder) and 4 (ice). Finally, for the desired performance criteria, the possible values are between 0 (lower criterion) and 3 (most important criterion).

Table 2.
Coefficient of relations in N-dimensions to predict properties of the preferred ski with p-values of theses coefficients in parenthesis.
The correlations for predicting the properties of the preferred skis for each skier are stronger than those for predicting the behaviour of a given ski. In this case, multivariate analysis brings many interesting new relationships. For example, three of the four properties of skis are greatly influenced by preference for forgiveness. Based on these results, a forgiving ski is stiff in bending and torsion, but with a low camber.
4. Conclusions
This paper analyzes the data from the on-snow evaluation of 12 pairs of skis, of constant geometry but varying stiffnesses, by 23 participants. Two analyzes were carried out to better understand the relation between the stiffness properties, the skier profiles and the on-snow performance. In the first analysis, it was shown that torsional stiffness, bending stiffness, mass and camber was a significant predictor of the ease of initiating a turn, versatility and performance in short turn. This information could be used by a salesman to recommend a ski that corresponds to the on-snow experience that a customer is looking for.
The second analysis connects the skiers’ favorite ski’s properties directly to its skier’s profile. This profile can easily be collected through a simple questionnaire. This analysis has shown that there are strong multidimensional relationships that can be used to predict the preferred ski of a skier. These results could easily be implemented as an online personalized recommendation tool to guide the skiers toward the skis that they are the most likely to prefer.
The results presented in this paper demonstrate the relationships can be found between mechanical properties, skier profiles and on-snow experiences. To correctly inform customers or ski designers, more data should be collected to strengthen the relationships found. For example, a larger number of skier should try the skis in different snow conditions. Furthermore, other parameters such as geometry and damping should be included in the analysis. These additional parameters are important to predict a greater variety of on-snow feelings that are not fully represented by bending stiffness, torsional stiffness, camber and mass.
Acknowledgments
This work was supported by the Natural Sciences and Engineering Research Council of Canada (NSERC) and the Fonds de Recherche Nature et Technologies du Québec (FRQNT). The authors also thank the Mont-Ste-Anne Ski Resort for providing ski tickets to all the participants in this study and Xalibu Skis Conception for the design of the skis.
References
- Howe, J. Skiing Mechanics, 1st ed.; Poudre Press: Laporte, CO, USA, 1963; pp. 9–28. [Google Scholar]
- Nachbauer, W.; Rainer, F.; Schindelwing, K.; Kaps, P. Effects of ski stiffness on ski performance. In The Engineering of Sports 5; International Sports Engineering Association: Sheffield, UK, 2004; Volume 5, pp. 472–479. [Google Scholar]
- Federoff, P.; Auer, M.; Fauve, M.; Luthi, A.; Rhyner, H. Subjective evaluation of the performance of alpine skis and correlations with mechanical ski properties. In Engineering of Sport 6; Springer: Berlin/Heidelberg, Germany, 2006; Volume 6, pp. 287–292. [Google Scholar]
- Fisher, C.; Overney, L.S.; Fauve, M.; Blanke, O.; Rhyner, H.; Herzog, M.H.; Bourban, P.E.; Månson, J.A. What static and dynamic properties should slalom skis possess? Judgements by advanced and expert skiers. J. Sports Sci. 2007, 14, 1567–1576. [Google Scholar] [CrossRef] [PubMed]
- Truong, J.; Brousseau, C.; Lussier Desbiens, A. A Method for Measuring the Bending and Torsional Stiffness Distributions of Alpine Skis. Procedia Eng. 2016, 147, 394–400. [Google Scholar] [CrossRef][Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).