Abstract
Excessive heat at the foot-shoe sole interface negatively affects a human’s thermal comfort. An understanding of the thermal behavior at this interface is important for alleviating this discomfort. During gait motion, a human’s body weight cyclically compresses a shoe sole (commonly constructed of viscoelastic materials), generating heat during loading. To evaluate the thermal effects of this internal heat generation on foot comfort, we developed and empirically validated a thermal analysis model during gait motion. A simple, one-dimensional prediction model for heat conduction with heat generation during compressive loading was used. Heat generation was estimated as a function of the shoe sole’s material properties (e.g., elastic modulus) and various gait parameters. When compared with experimental results, the proposed model proved effective in predicting thermal behavior at the foot-shoe sole interface under various conditions and shows potential for improving a human’s thermal comfort during gait motion through informed footwear design.
Published: 14 February 2018
1. Introduction
Footwear designs have continued to advance in an effort to improve comfort and performance in routine daily or specialized sports applications. Despite these known advancements, few studies were uncovered that considered the thermal comfort of footwear. A human foot acts as a thermal radiator for the body [1]. When a foot is confined in a shoe, the heat that is prevented from releasing can negatively affect a human’s thermal comfort. This effect is exacerbated during gait motion. Shoe soles are commonly constructed from viscoelastic materials, such as ethylene-vinyl acetate (EVA), to provide shock buffering. These same materials generate heat when they are compressed by loading [2], adding to a human’s discomfort. An understanding of the thermal behavior at the foot-shoe sole interface is important for alleviating this discomfort.
Thus, the objective of this study was to investigate the microclimatic thermal effects attributable to internal heat generation at the foot-shoe sole interface during gait motion. First, we determined the mechanical parameters associated with gait. Next, we developed a simple heat transfer model for predicting temperature at the foot-shoe sole interface by considering both the human’s metabolic heat generation and the shoe sole’s heat generation under contact loading. Finally, we validated the proposed heat transfer model empirically.
2. Materials and Methods
2.1. Analysis of Gait Motion
As a first step in this study, we determined the mechanical parameters associated with gait. When a foot contacts a shoe sole, the mechanical energy of loading is transformed into thermal energy associated with the shoe sole deformation. To determine the effects of gait on this phenomenon, parameters related to foot loading were directly measured. As previously reported, the foot contact loading and contact area are time-dependent [3]. As such, we first considered the effects of gait speed on time-dependent changes in the amount of loading force, contact area, and timing. The loading force and contact area were measured using the pressure sensors (Nitta, F-scan System). Gait speeds of 3 (walking), 6 (walking), and 9 km/h (running) were tested.
2.2. Development of the Proposed Thermal Analysis Model
After determining the mechanical parameters associated with gait, we developed a simple heat transfer model for predicting temperature at the foot-shoe sole interface during gait motion. Figure 1 shows the one-dimensional coordinate system used in the model. In the proposed model, heat is primarily transferred by conduction. Especially for human body, Penne’s bioheat transfer equation was used. The unsteady-state heat transfer relationships for the shoe sole (constructed of EVA rubber) under contact loading and the human are expressed as follows:
where T is the temperature [K], t is the time [s], ρ is the density [kg/m3], c is the specific heat [J/(kgK)], k is the thermal conductivity [W/(mK)], qr is the shoe sole’s heat generation under contact loading [W/m3] and is the human’s metabolic heat generation [W/m3]. The subscripts r, f, and a indicate the shoe sole with EVA rubber, the human foot, and the arteria, respectively.
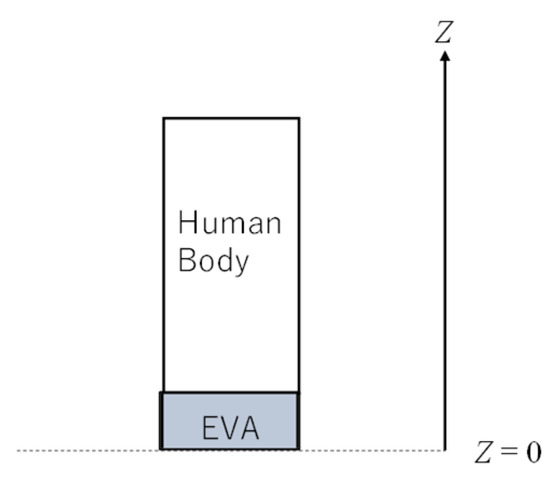
Figure 1.
One-dimensional coordinate system used in the proposed thermal analyses model.
The heat gain at the foot-shoe sole interface attributable to loading is equal to the energy loss caused by shoe sole deformation during foot contact. During swing, heat is released from the rubber sole by forced convection due to foot movement. Because gait motion is cyclic, the heat generated during a single gait cycle can be expressed as follows [3]:
where W is the per gait cycle energy loss [N], S is the foot contact area [m2], L is the foot contact duration [s], ε0 is the strain amplitude, E′′ is the elastic modulus loss [Pa], and h is the convective heat transfer coefficient [W/(m2·K)]. The subscripts env indicates ambient environment. The energy loss is assumed to be fully transformed into thermal energy.
Using the proposed thermal analysis model, heat generation was estimated as a function of various gait parameters and the shoe sole’s material properties (e.g., elastic modulus). Table 1 details the three shoe sole materials considered in the study. Each was a specially blended EVA with known material properties. In general, EVA08 is a harder material while EVA16 is a softer material. The materials’ strain during gait motion is also an important parameter for predicting heat generation based on Equation (4). As such, strain was measured for each material during gait motion using a three-dimensional motion and deformation sensor (GOM, ARAMIS) with a sampling frequency of 15 Hz.

Table 1.
Shoe sole material properties.
2.3. Empirical Validation of the Proposed Thermal Analysis Model
Following development of the proposed thermal analysis model, its ability to predict thermal behavior (specifically heat transfer and vertical temperature distributions) at the foot-shoe sole interface during gait motion was empirically validated. Nine human subjects with heights of 1.70 ± 0.04 m, weights of 59.8 ± 5.4 kg, and ages of 23.0 ± 0.8 years provided informed consent to participate in this study. Body weights among the participants were roughly equivalent, minimizing the effects of body weight on the degree of loading and allowing for results averaging across all participants.
Experiments were conducted in an artificial climate chamber that enabled arbitrary climatic conditions. To limit a shoe’s insulating effects, a 15-mm thick EVA rubber sole sans shoe was prepared and attached to each participant’s foot. Temperatures were measured vertically using thermocouples in 5-mm increments. To support averaging, temperatures were measured at three points along each surface. For the human foot, the ball, arch, and heel were selected for measurement. Figure 2 conceptually depicts these temperature measurement locations. Participants’ O2 intake and CO2 production were also measured to support metabolic heat generation estimation.
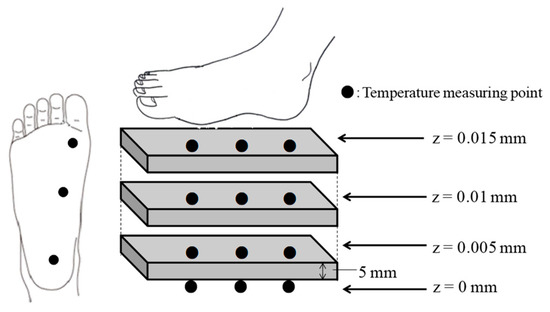
Figure 2.
Conceptual diagram of temperature measurement locations.
3. Results
3.1. Input Parameters for the Proposed Thermal Analysis Model
The proposed thermal analysis model requires both gait motion and material property parameters to predict heat transfer and generation. Required gait motion parameters include the foot contact area, foot contact duration, and gait cycle duration. Required material property parameters include the strain.
3.1.1. Gait Motion Parameters
In this study, the required gait motion parameters were determined empirically. Figure 3 shows the mean contact area under loading [Figure 3a] and the stance and swing durations [Figure 3b] as a function of gait frequency. This study focuses on the force-thermal energy interaction. The use of gait frequencies better supports consideration of heat generation in equations focused on contact loading. In this study, gait speeds of 3, 6, and 9 km/h corresponded to gait frequencies of 45, 60, and 75 beats/min from preliminary experiments. In general, gait frequency increases linearly with gait speed.
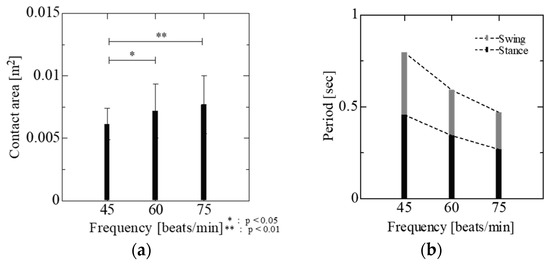
Figure 3.
Measured mean gait parameters as a function of gait frequency: (a) Contact area; (b) Stance and swing durations.
Experimental results indicated that the contact area increased as gait speed increased, measuring 0.0061, 0.0072, and 0.0077 m2 at gait frequencies of 45, 60, and 75 beats/min, respectively. Significant contact area differences were confirmed between the 45 and 60 beats/min and the 45 and 75 beats/min gait frequencies. Conversely, the stance and swing durations decreased as gait speed increased. For example, stance time was 0.46, 0.34, and 0.27 s at gait frequencies of 45, 60, and 75 beats/min, respectively.
3.1.2. Material Property Parameters
In this study, the required material property parameters were also determined empirically. Table 2 lists the mean maximum strains for the different EVA materials and gait frequencies considered. The strain increased as the EVA rubber softness and gait frequency increased. Figure 4 shows the measured strain for the EVA16 material at a gait frequency of 60 beats/min. A negative value indicates compression. The upper layers of the sole exhibited the highest strains. The maximum measured strain was approximately 2.0 mm.

Table 2.
Measured mean maximum strains for different EVA materials and gait frequencies.
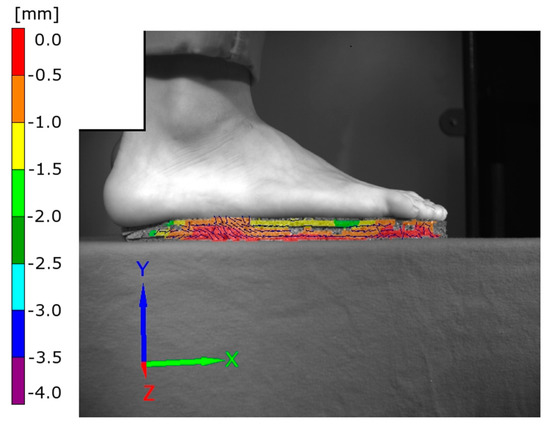
Figure 4.
Measured strain for the EVA16 material at a gait frequency of 60 beats/min.
3.2. Thermal Analysis
3.2.1. Empirical Temperature Distributions
Time-dependent temperature distributions at the foot-show sole interface were determined empirically in this study. Figure 5 show the time-dependent temperature distribution for the EVA08 material under a neutral thermal environment of 25 °C and for various gait frequencies. The values presented are obtained as the mean values of all participants. As a baseline reference, Figure 5a shows the temperature distributions at a frequency gait of 0 km/h (seated position). When the human subject was seated, all temperatures remained constant and a thermally neutral state was reached. When the human subject began walking, temperatures increased over time and increased with gait frequency. A faster gait resulted in higher temperatures. The upper layers of the sole exhibited higher temperatures because of the higher deformations (higher strains) and direct contact with the human foot. For example, temperatures measured 0.5 and 2.6 °C at the bottom (z = 0) and top (z = 0.02) of the shoe sole at a gait frequency of 75 beats/min. Temperature distributions for the other EVA materials showed similar trends.
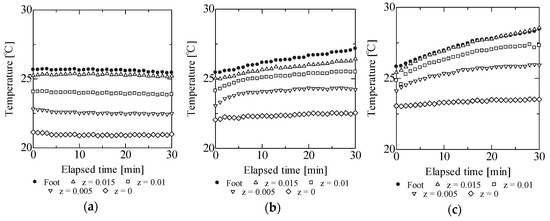
Figure 5.
Measured time-dependent temperature distributions for the EVA08 material at 25 °C: (a) 0 beats/min gait frequency (seated position); (b) 45 beats/min gait frequency; (c) 75 beats/min gait frequency.
3.2.2. Comparative Measured and Predicted Temperature Distributions
As a final step in this study, we compared the time-dependent temperature distributions obtained empirically with the temperature distributions predicted by the proposed thermal analysis model. Figure 6 compares the measured and predicted time-dependent temperature distributions on the bottom of human foot for the EVA08 material at 25 °C and various gait frequencies. As noted previously, the required parameters to support the model, including the prediction of initial temperatures, were obtained empirically. In this comparison, data from a single individual were used. Both measured and predicted temperatures increased over time. After 30 min, predicted temperatures were elevated 3.6 and 6.2 °C for gait frequencies of 45 and 75 beats/min, respectively. Comparatively, measured temperatures were elevated 3.9 and 7.0 °C for gait frequencies of 45 and 75 beats/min, respectively. This same level of agreement was observed across all conditions considered in this study. Thus, the proposed model proved effective in predicting thermal behavior at the foot-shoe sole interface during gait motion under various conditions.
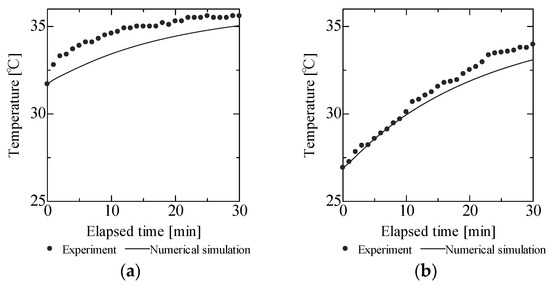
Figure 6.
Comparative measured and predicted time-dependent temperature distributions for the EVA08 material at 25 °C: (a) 45 beats/min gait frequency; (b) 75 beats/min gait frequency.
4. Conclusions
Thermal comfort is an important but often overlooked feature when designing footwear. In this study, we developed and empirically validated a thermal analysis model during gait motion. First, we determined the mechanical parameters associated with gait. Next, we developed a simple heat transfer model for predicting temperature at the foot-shoe sole interface by considering both the human’s metabolic heat generation and the shoe sole’s heat generation under contact loading. Finally, we validated the proposed heat transfer model empirically. When compared with experimental results, the proposed model proved effective in predicting thermal behavior at the foot-shoe sole interface under various conditions. This development is significant because of its potential for improving a human’s thermal comfort during gait motion through informed footwear design. Future research will consider the overall footwear comfort including the inner and the upper areas but not limited to the foot-shoe sole interface.
Acknowledgments
The authors would like to acknowledge Chugoku Rubber Industry Co., Ltd. for providing sample materials and relevant technical assistance in support of this study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Taylor, N.A.S.; Machado-Moreira, C.A.; van den Heuvel, A.M.J.; Caldwell, J.N. Hands and feet: physiological insulators, radiators and evaporators. Eur. J. Appl. Physiol. 2014, 114, 2017–2060. [Google Scholar] [CrossRef] [PubMed]
- Terasaki, K.; Okada, M.; Matsuura, K.; Kawashimo, K.; Maeda, Y.; Kitazawa, K. Heat generation and transient heat conduction of rubber under cyclic compressing. Trans. Jpn. Soc. Mech. Eng. 1976, 42, 3533–3540. [Google Scholar] [CrossRef]
- Shimazaki, Y.; Murata, M. Effect of gait on formation of thermal environment inside footwear. Appl. Ergon. 2015, 49, 55–62. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).