Kinematic Differences between Set- and Jump-Shot Motions in Basketball †
Abstract
:1. Introduction
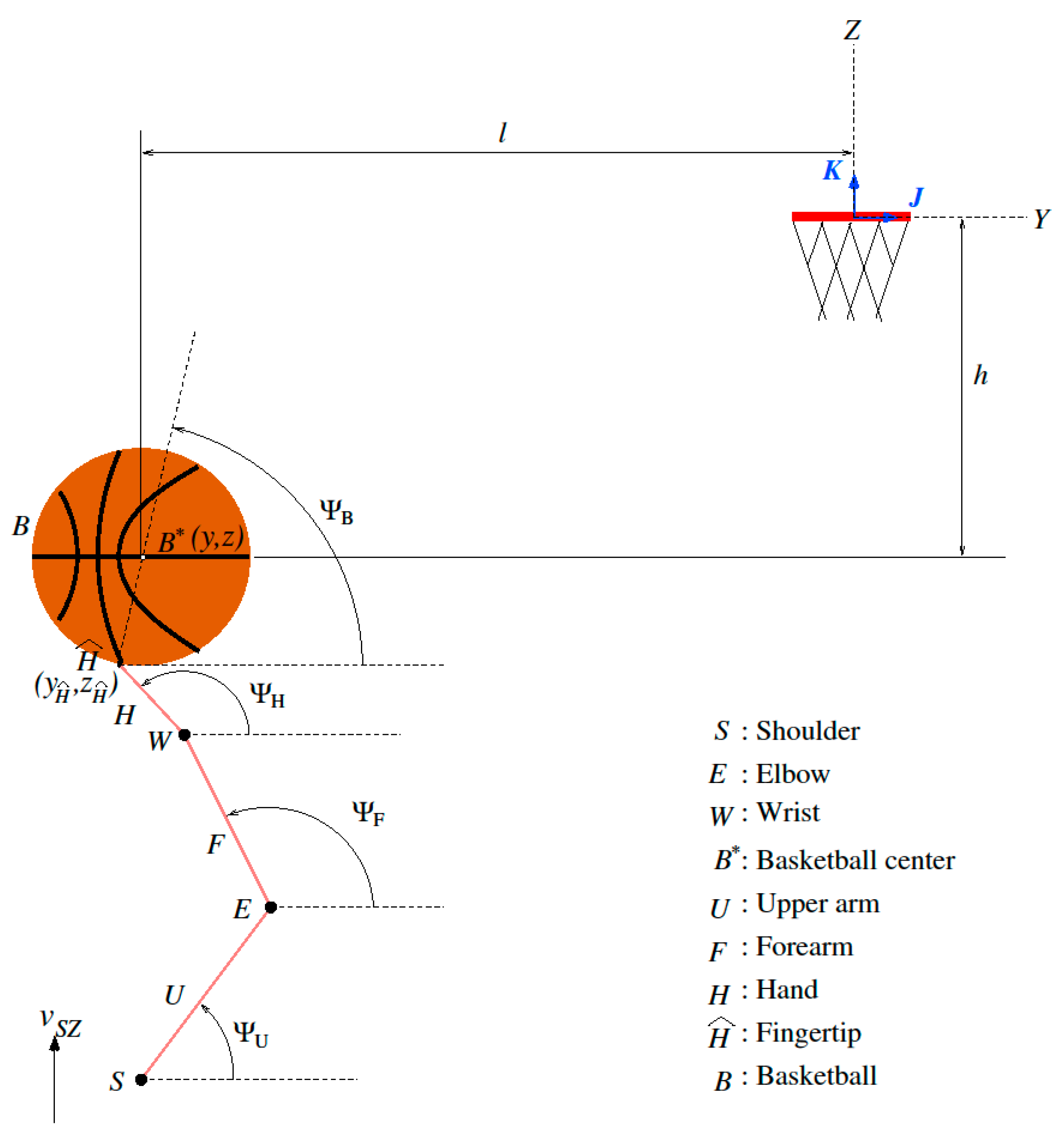
2. Kinematic Model for Shots, Assumptions and Simulation Parameters
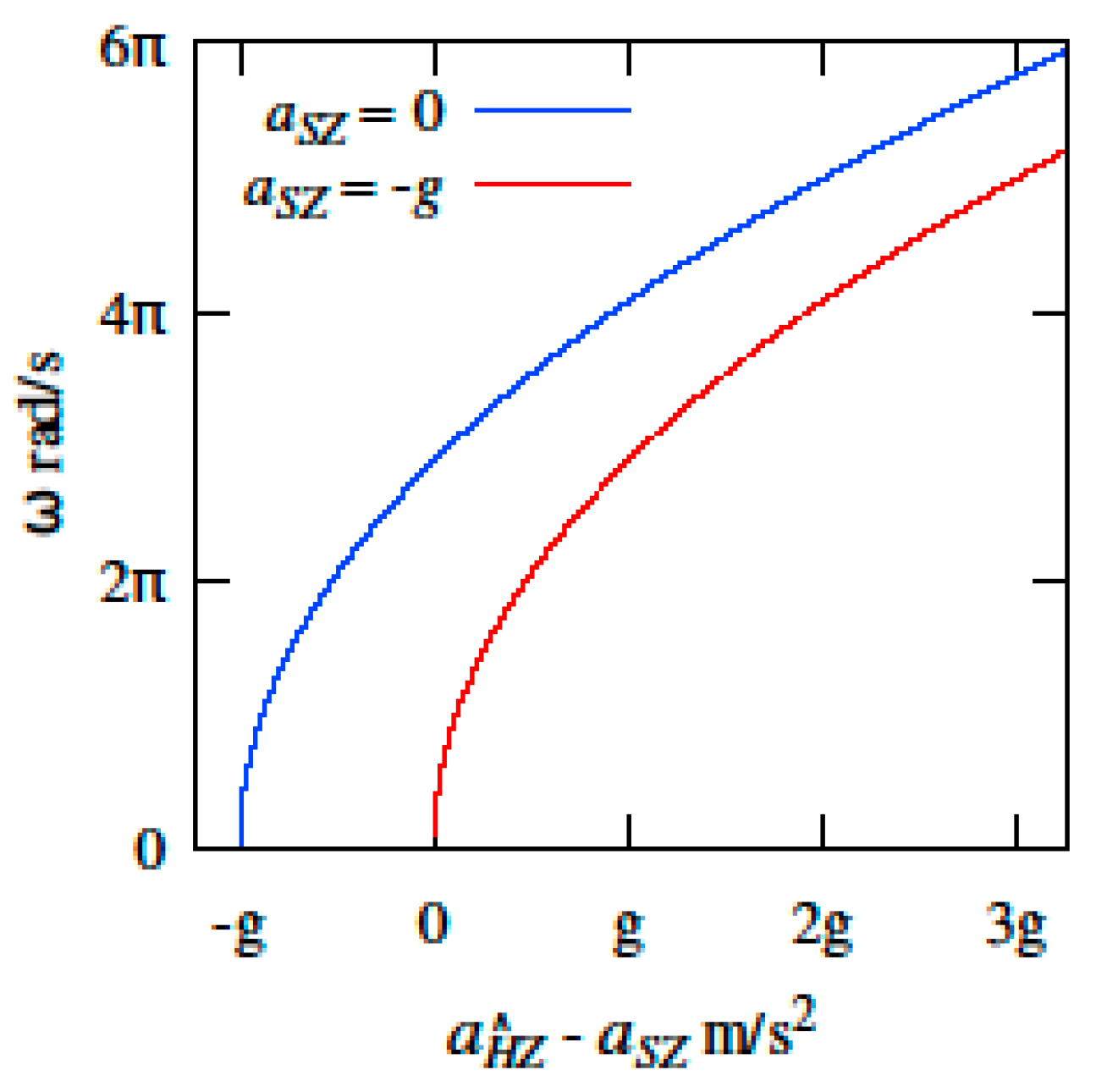
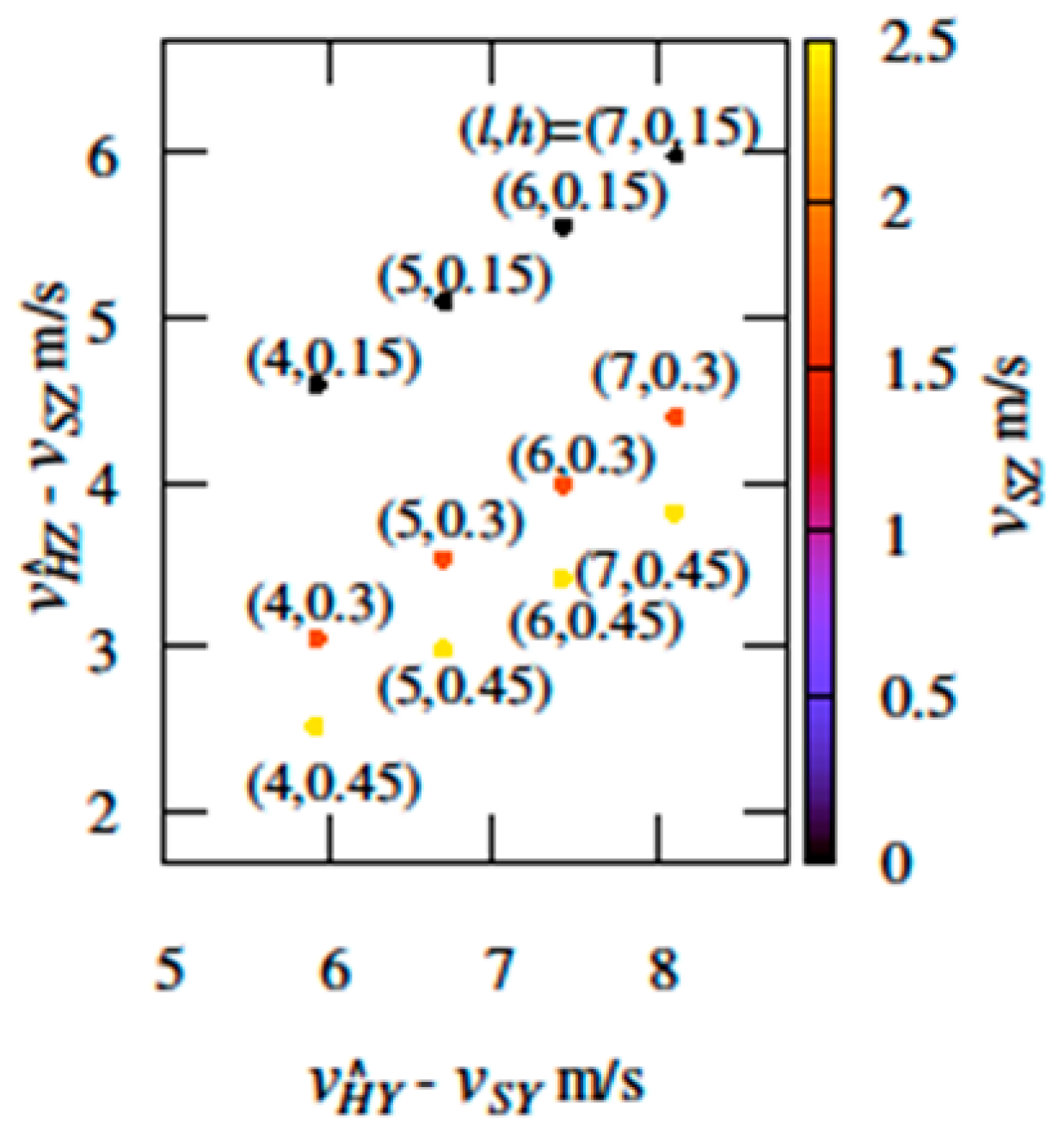
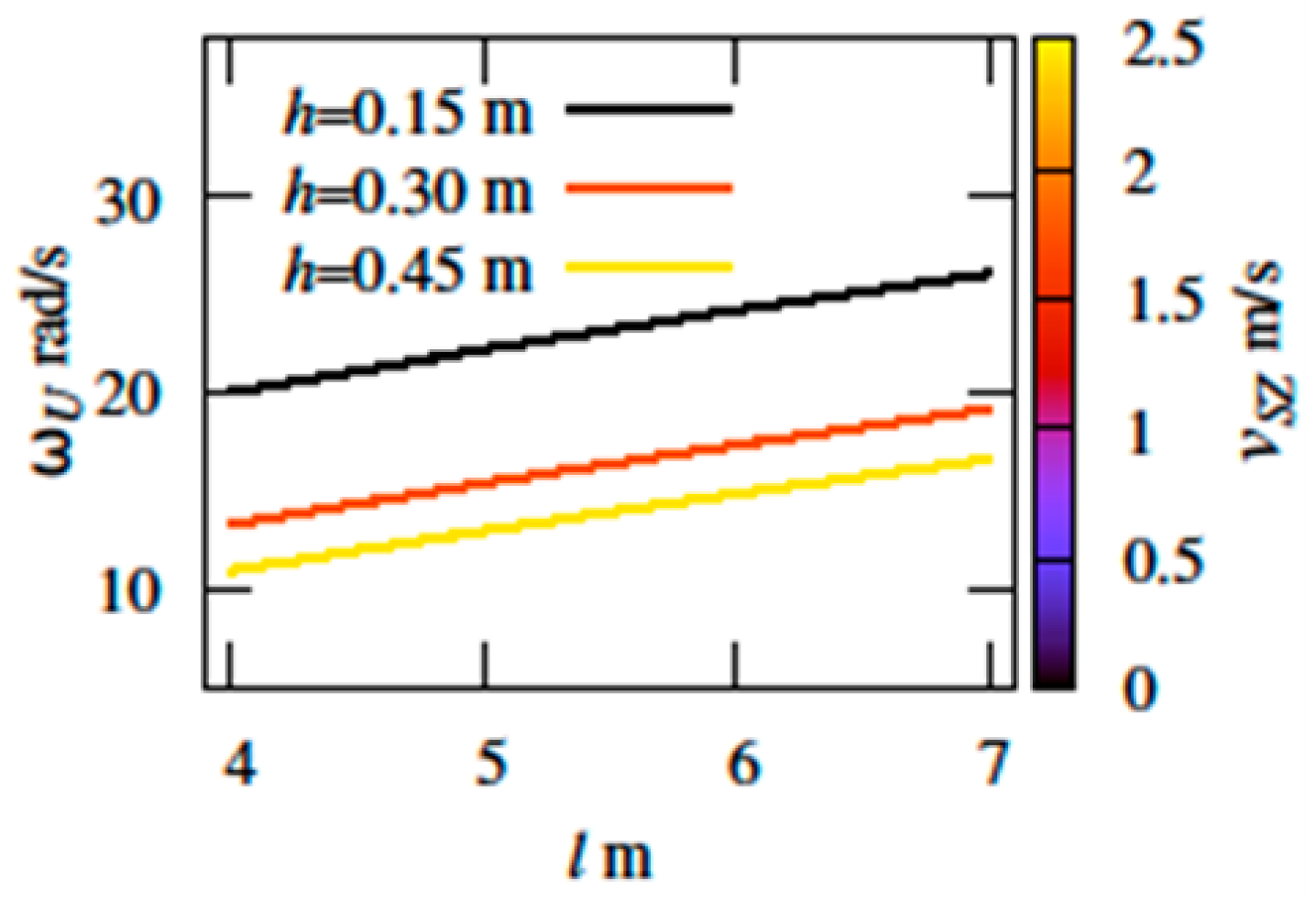
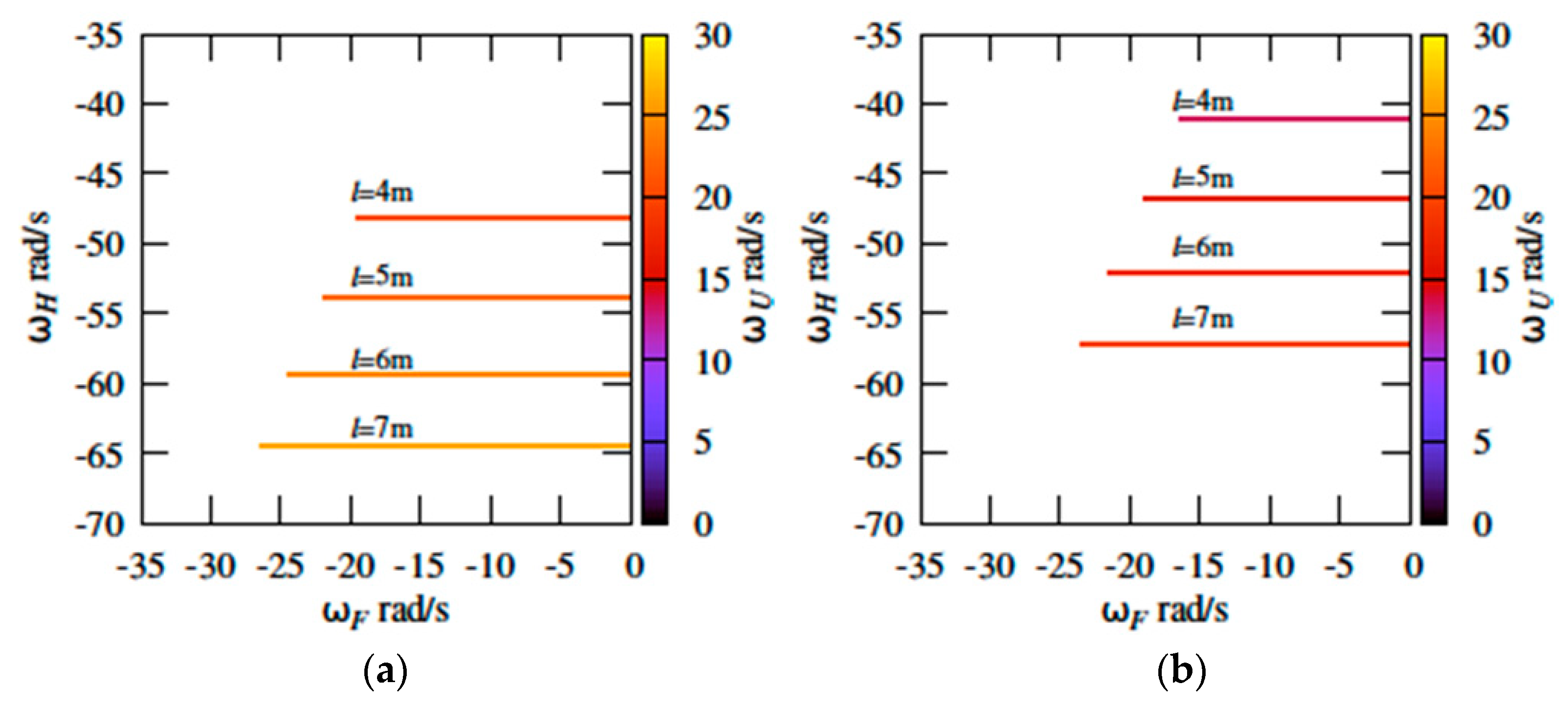
3. Results and Discussion
4. Conclusions
Conflicts of Interest
References
- Cooper, J.M.; Siedentop, D. The Theory and Science of Basketball, 2nd ed.; Lea & Febiger: Philadelphia, PA, USA, 1975; pp. 64–71. [Google Scholar]
- Satern, M. Basketball: Shooting the jump shot. Strategies 1988, 1, 9–11. [Google Scholar] [CrossRef]
- Knudson, D. Biomechanics of the basketball jump shot –Six key teaching points. J. Phys. Educ. Recreat. Dance 1993, 64, 67–73. [Google Scholar] [CrossRef]
- Miller, S.; Bartlett, R. The effects of increased shooting distance in the basketball jump shot. J. Sports Sci. 1993, 11, 285–293. [Google Scholar] [CrossRef] [PubMed]
- Miller, S.; Bartlett, R. The relationship between basketball shooting kinematics, distance and playing position. J. Sports Sci. 1996, 14, 243–253. [Google Scholar] [CrossRef] [PubMed]
- Okazaki, V.H.A.; Rodacki, A.L.F. Increased distance of shooting on basketball jump shot. J. Sports Sci. Med. 2012, 11, 231–237. [Google Scholar] [PubMed]
- Tsarouchas, E.; Kalamaras, K.; Giavroglou, A.; Pressas, S. Biomechanical analysis of free shooting in basketball. In Proceedings of the 6th International Society of Biomechanics in Sports Symposium; Kreighbaum, E., McNeill, A., Eds.; International Society of Biomechanics in Sports: Bozeman, MT, USA, 1990; pp. 551–560. [Google Scholar]
- Schwark, B.N.; Mackenzie, S.J.; Springings, E.J. Optimizing the release conditions for a free throw in wheelchair basketball. J. Appl. Biomech. 2004, 20, 153–166. [Google Scholar]
- De Leva, P. Adjustments to Zatsiorsky-Seluyanov’s segment inertia parameters. J. Appl. Biomech. 1996, 29, 1223–1230. [Google Scholar] [CrossRef]
- Okubo, H.; Hubbard, M. Kinematics of arm joint motions in basketball shooting. Procedia Eng. 2015, 112, 443–448. [Google Scholar] [CrossRef]
- Brancazio, P.J. The physics of basketball. Am. J. Phys. 1981, 49, 356–365. [Google Scholar] [CrossRef]
- Okubo, H.; Hubbard, M. Comparison of shooting arm motions in basketball. Procedia Eng. 2016, 147, 133–138. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Okubo, H.; Hubbard, M. Kinematic Differences between Set- and Jump-Shot Motions in Basketball. Proceedings 2018, 2, 201. https://doi.org/10.3390/proceedings2060201
Okubo H, Hubbard M. Kinematic Differences between Set- and Jump-Shot Motions in Basketball. Proceedings. 2018; 2(6):201. https://doi.org/10.3390/proceedings2060201
Chicago/Turabian StyleOkubo, Hiroki, and Mont Hubbard. 2018. "Kinematic Differences between Set- and Jump-Shot Motions in Basketball" Proceedings 2, no. 6: 201. https://doi.org/10.3390/proceedings2060201
APA StyleOkubo, H., & Hubbard, M. (2018). Kinematic Differences between Set- and Jump-Shot Motions in Basketball. Proceedings, 2(6), 201. https://doi.org/10.3390/proceedings2060201



