The Influence of Outdoor Shoe Sole Stiffness on the Metatarsophalangeal Joint Kinematics When Walking and Running in Different Conditions ^†

Abstract

Understanding the action of the metatarsophalangeal joint (MTP) is fundamental to improving the design process of a new outdoor shoe. Coming from the stated consideration, the aim of this research is to study the influence of shoe sole stiffness and terrain slope on the MTP joint angle of subjects walking in different conditions. To pursue this intent, different data collection sessions have been carried out in-vitro and in-vivo, indoor and outdoor. Two different approaches have been used to collect gait kinematics: an IMU (Inertial Measurement Unit) based system for the first campaign of tests, and a 2D video analysis for the second. Major findings showed a linear correlation between shoe sole stiffness and peak MTP joint angle during gait, as well as consistency in the value of the slope of the linear regression curves corresponding to the different conditions examined.

1. Introduction

Many studies have been carried out in the development and optimization of outdoor shoes. One of the major ambitions in the footwear design process is the possibility of applying a Quality Function Deployment (QFD) approach [1,2,3] in order to quantitatively evaluate the possible correlations between shoes Quality Requirements (QR, such as comfort or safety), as expressed by the customers, and Constructive Technologies (CT, such as sole material or thickness), as managed by the manufacturers. The shoe’s Engineering Characteristics (EC, such as sole stiffness or energy absorption), as quantified in standard laboratory tests, can be seen as the link between the fields of QR and CT. Since the design phase requires numerical and measurable quantities, engineers have to work on EC and CT, and find correlations between these types of parameters.

Most studies involving gait analysis ignore the contribution of metatarsophalangeal (MTP) joint. However, the studies of Stefanyshyn and Nigg [4] proved that the MTP is a large energy absorber during running and sprinting. The importance of the MTP has been also underlined by the studies of Arndt et al. [5], in which they correlated the increased second metatarsal stress fracture with the adoption by military recruits in Sweden of a new type of boot with a more flexible sole. Furthermore Roy and Stefanyshyn [6] investigated the running metabolic economy of a group of subjects wearing shoes with soles of different stiffness values. They demonstrated that the shoe sole stiffness is an important parameter that has to be taken into consideration when examining the metabolic efficiency of walking and running.

From this perspective, the aim of this study was to examine the effect of shoe sole stiffness and terrain slope on the MTP joint angle of subjects walking in different conditions.

2. Materials and Methods

2.1. Shoes Tested

Three types of shoes of the same brand with different specific sport applications, and consequently different construction features, were examined in this research (Figure 1). The first type of footwear is designed for trail running and therefore will be called Trail Running (TR), the second one is designed for hiking at high speed, and for this reason will be called Fast Hiking (FH), and the last one is for endurance hiking, and is therefore called Classic Hiking (CH).

2.2. Footwear Stiffness Determination

The determination of the sole flexing (i.e., longitudinal bending) stiffness of the outdoor shoes was carried out at testing facilities of the company Dolomiticert (Longarone, Italy) in accordance with EN ISO 20344:2011 [7]. The setup of the test and its schematic representation are shown in Figure 2a,b. Three pairs of shoes (EU 42, 43 and 44) were tested for each model of footwear.

The mean results of the stiffness test are plotted in Figure 2c. Sole stiffness was defined as the slope of the secant passing through the curves between 0 and 10 degrees ($K_{Fs10}^{MTP}$). This is due to the fact that, from this angle on, the slope of the curve becomes almost constant (lower limit), and all the three types of shoes tested reached the MTP flexion of 10 degrees (upper limit). The numerical values are shown in Table 1, together with the other results of this research.

.

2.3. First Test Session: Indoor, In-Vivo

The first indoor kinematic analysis was carried out at the Sports & Rehabilitation Engineering Laboratory of the Department of Industrial Engineering of Padova (Padova, Italy). Prior to data collection, the reliability of the kinematic data coming from the IMU based protocol (MTw Awinda, XSens Technologies, Enschede, The Netherlands) was tested thanks to a direct comparison with an optoelectronic Motion Capture system (Smart-DX 6000, BTS Bioengineering, Milan, Italy). During the data capture sessions, each of the four volunteering subjects was equipped with 3 wireless 3D IMU sensors recording the absolute angular motion of the shank, rearfoot and forefoot respectively (Figure 3a).

After warming up, each subject (males, 24 ± 2 years old, 1.81 ± 0.02 m, 76.3 ± 8.7 kg) walked at a fixed speed of 5 km/h on a treadmill of variable inclination (Artis^® Run, Technogym) for 8 min. Starting from 0%, the slope of the treadmill was increased by 5% every 2 min, spanning the inclination from 0% to 15%. Each subject repeated the same acquisition session wearing the three types of footwear under analysis.

Even though 3D data were collected and despite the fact that the MTP joint axis is oblique, for the sake of simplicity, a 2D kinematic analysis was performed focusing only on the sagittal plane in a first approximation. The 2D joint relative flexion angles were obtained by proper difference between the absolute angles provided by the IMU sensors. We chose to set the MTP joint angle to zero when the subject is in the static standing posture wearing the shoes. Data were collected wirelessly with a sampling rate of 60 Hz and for a time span of 60 s for each combination of shoe type and slope.

2.4. Second Testing Session: Outdoor, In-Vivo

A second campaign of data collection was carried out outdoor in San Vito di Cadore (Belluno, Italy). The data collection was performed on one subject (male, 42 years old, 1.80 m, 77 kg) climbing at slow self-selected speed and at fast speed on a flight of stairs (tread 285 mm, riser 165 mm).

Since there were some zero drift issues with the IMU sensors in the outdoor environment, we chose to combine in redundancy this data acquisition system with another one, based on video motion analysis. Consequently, the kinematics data were collected both with the IMU system previously described and with a high-speed camera (MotionBLITZ EoSens Cube, Mikrotron, Unterschleißheim, Germany) at a sampling rate of 200 Hz.

To improve the effectiveness of the automatic point tracking of the video analysis software used (Tracker Video Analysis, Open Source Physics) four reflective markers were placed on locations relevant for the individuation of the joint angles of interest (Figure 3b). In the video analysis process the zero of the MTP angle was set as the minimum angle reached in the stance phase. The subject performed 3 trials for each of the three types of shoe under analysis and at 2 speed levels, for a total of 18 trials.

Figure 3. Data collection sessions: (a) example of data collection of one subject wearing TR shoes, walking at 5 km/h on a treadmill with an inclination of 5%; (b) example of data collection of one subject wearing CH shoes climbing a flight of stairs outdoor. Both IMU and video based acquisition systems were used together.

Figure 3. Data collection sessions: (a) example of data collection of one subject wearing TR shoes, walking at 5 km/h on a treadmill with an inclination of 5%; (b) example of data collection of one subject wearing CH shoes climbing a flight of stairs outdoor. Both IMU and video based acquisition systems were used together.

3. Results

3.1. First Testing Session

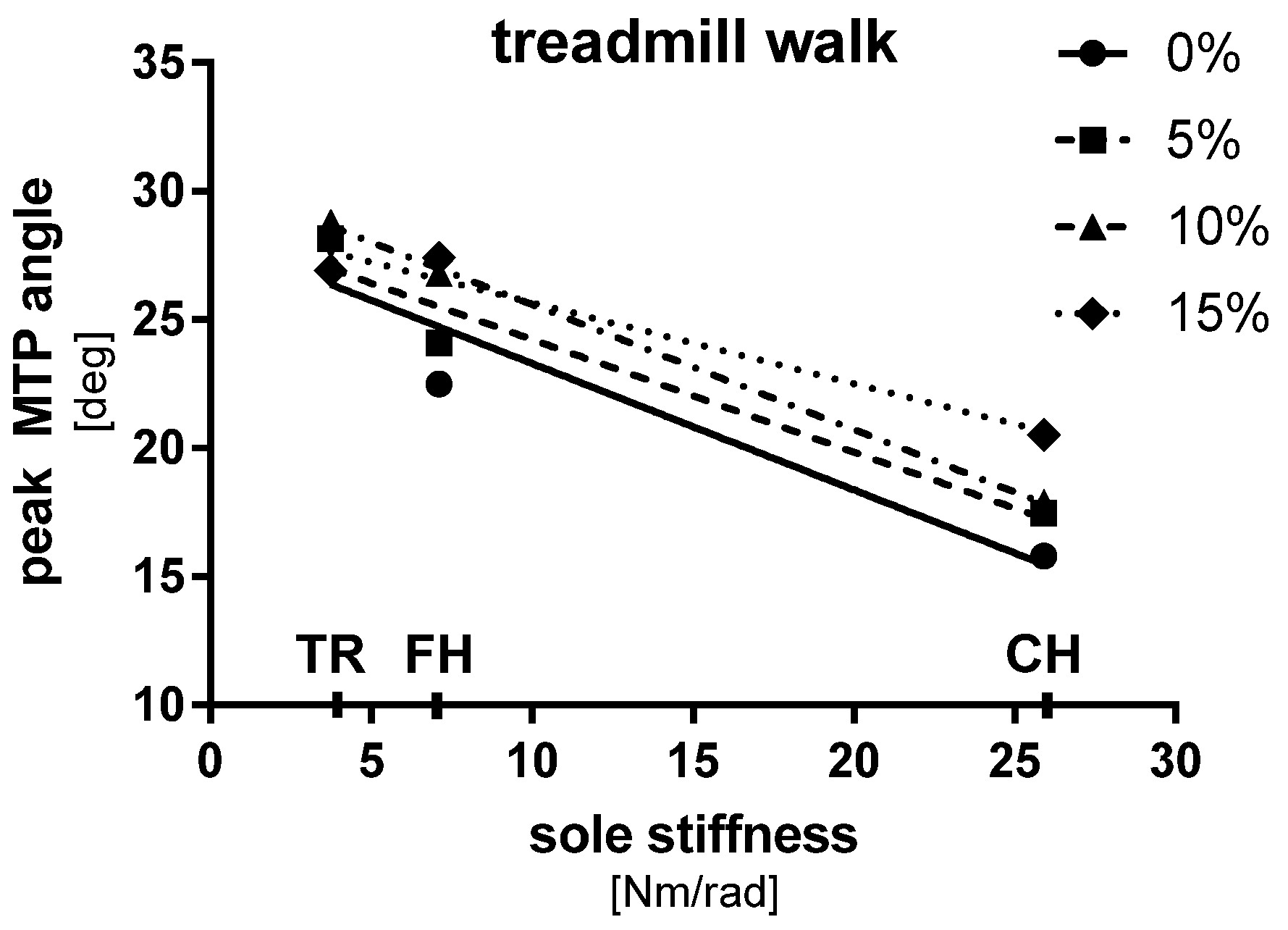
The main results of the first campaign of data acquisition are plotted in Figure 4. The graph is relative to the walking trials (5 km/h)). The x-axis represents the sole stiffness obtained with the method stated above, while the y-axis represents the average between subjects of the peak value of the mean (out of 5) MTP angle curve normalized to the gait cycle. The peak typically occurred in the push-off phase of the stance, when the power exchange of the MTP also reaches its maximum [4]. Two more features are reported in the figure: the first is the terrain slope parameter and the second is the linear regression curves corresponding to each slope.

A linear regression analysis (Graph Pad Prism 7, GraphPad Software, Inc.) was carried out for each one of the four slopes examined: by analyzing the coefficient of determination the quality of the fit was proven to be good for the walking trials ($R_{walk, 0\%}^2$ = 0.89, $R_{walk, 5\%}^2$ = 0.94, $R_{walk, 10\%}^2$ = 0.99, $R_{walk, 15\%}^2$ = 0.96). Furthermore the analysis concludes that the slopes of the different regression curves (0%, 5%, 10% and 15%) relative to the walking trials are not significantly different (p = 0.66 > 0.05 testing the null hypothesis that the slopes are all identical). Since the slopes are not significantly different, it is possible to calculate a unique slope for all the data of the walking session, that is -0.43. It means that, while the peak MTP angle decreases, the stiffness increases with a slope of 0.43 for all the terrain slopes examined in the treadmill walking trials.

A 2-way ANOVA analysis was performed for the walking trials, where the sole stiffness and the slope of the terrain were found to be significant sources of variation (p < 0.0001), together with their interaction.

3.2. Second Testing Session

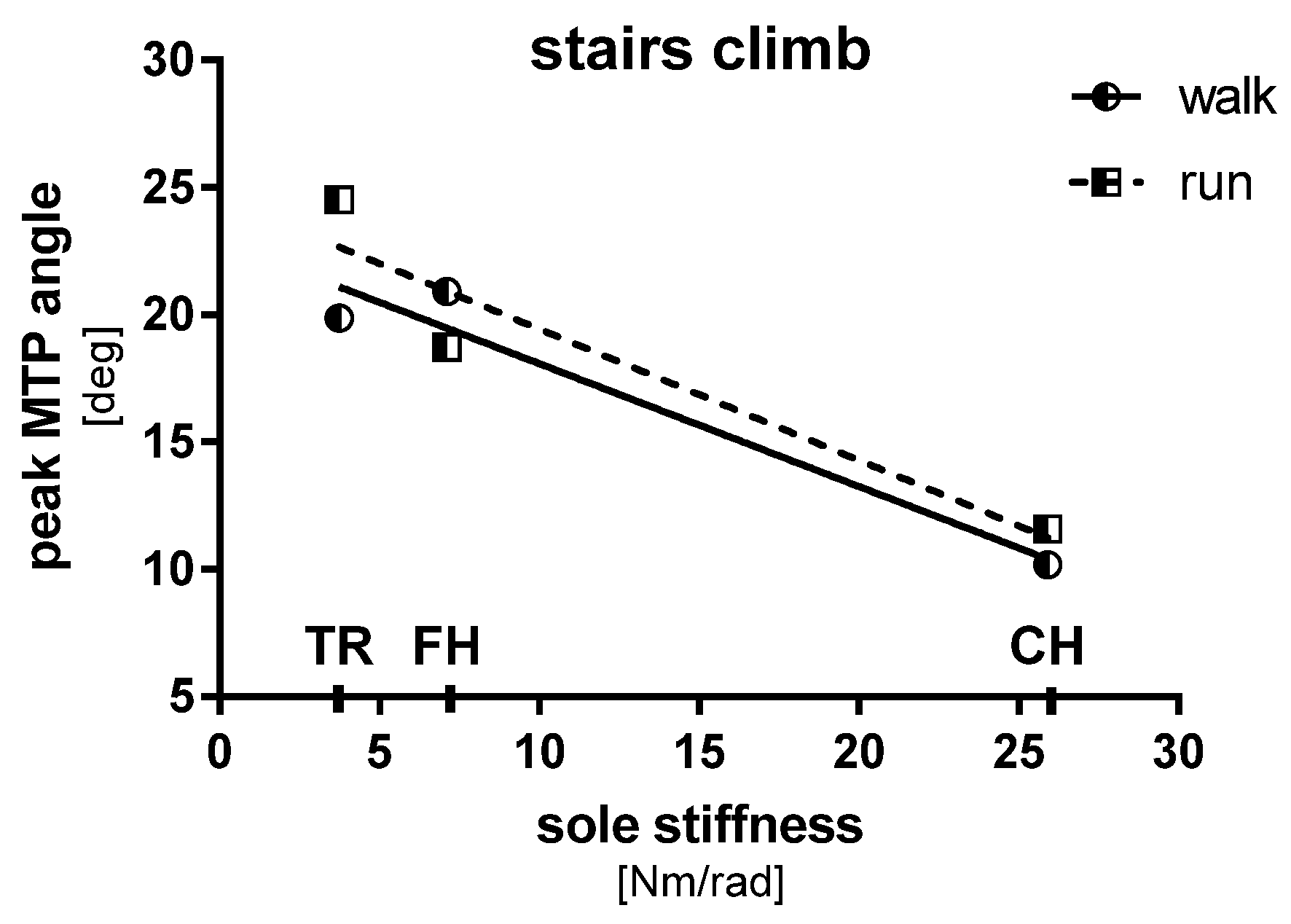
The graph reported in Figure 5 contains the peak value of the mean (out of 3) MTP angle curve normalized to the gait cycle versus the sole stiffness parametric in the stairs climbing speed.

Since the data coming from the IMU sensors showed significant derivation, we used only the data from the video analysis.

The linear regression analysis showed a good fitting characteristic for the 2 conditions ($R_{walk}^2$ = 0.95, $R_{run}^2$ = 0.90) and, again, since the slopes of the 2 regression lines are not significantly different (p = 0.88 > 0.05 testing the null hypothesis that the slopes are identical), it is possible to compute a unique linear regression curve with a slope of −0.50. Therefore, the peak MTP angle decreases as the stiffness increases, with a slope of 0.50 for a subject climbing stairs in the stated conditions.

The 2-way ANOVA analysis showed that the sole stiffness and the stairs climbing speed are significant sources of variation (p < 0.0001), together with their interaction.

3.3. Results Summary

The summary of the results achieved in this research are shown in Table 1 (mean ± SD).

Table 1. Results summary. The standard deviation of the peak MTP angle relative to the values of treadmill walk is calculated between subjects, while the one relative to the stair climb is calculated between repetitions of the same subject.

Footwear Name	Trail Running (TR)	Fast Hiking (FH)	Classic Hiking (CH)
Weight (EU 44) [g]	274	422	768
$\mathrm{Sole}\mathrm{stiffness}{K}_{Fs10}^{MTP}$ [Nm/rad]	3.75 ± 0.03	7.11 ± 0.16	25.90 ± 2.04
Treadmill (5 km/h)	peak MTP angle [deg]
Slope 0%	28.3 ± 0.5	22.5 ± 0.9	15.8 ± 0.3
Slope 5%	28.2 ± 0.7	24.1 ± 0.7	17.5 ± 0.5
Slope 10%	28.8 ± 0.9	26.8 ± 1.0	17.9 ± 0.5
Slope 15%	26.9 ± 1.3	27.4 ± 0.8	20.5 ± 0.3
Stairs	peak MTP angle [deg]
Walking	19.9 ± 0.4	20.9 ± 0.4	10.2 ± 0.6
Running	24.5 ± 1.1	18.7 ± 0.5	11.6 ± 0.7

Table 1. Results summary. The standard deviation of the peak MTP angle relative to the values of treadmill walk is calculated between subjects, while the one relative to the stair climb is calculated between repetitions of the same subject.

Footwear Name	Trail Running (TR)	Fast Hiking (FH)	Classic Hiking (CH)
Weight (EU 44) [g]	274	422	768
$\mathrm{Sole}\mathrm{stiffness}{K}_{Fs10}^{MTP}$ [Nm/rad]	3.75 ± 0.03	7.11 ± 0.16	25.90 ± 2.04
Treadmill (5 km/h)	peak MTP angle [deg]
Slope 0%	28.3 ± 0.5	22.5 ± 0.9	15.8 ± 0.3
Slope 5%	28.2 ± 0.7	24.1 ± 0.7	17.5 ± 0.5
Slope 10%	28.8 ± 0.9	26.8 ± 1.0	17.9 ± 0.5
Slope 15%	26.9 ± 1.3	27.4 ± 0.8	20.5 ± 0.3
Stairs	peak MTP angle [deg]
Walking	19.9 ± 0.4	20.9 ± 0.4	10.2 ± 0.6
Running	24.5 ± 1.1	18.7 ± 0.5	11.6 ± 0.7

4. Discussion

Overall, all four subjects employed in the indoor session reached values of peak MTP angle that did not show any significant deviation from the average (SD < 1.3°).

The statistical analysis confirmed that there is a strong influence of the shoe sole stiffness and terrain slope on the peak MTP angle reached in the treadmill walking trials, and of the shoe sole stiffness and speed of climbing for the stair climbing trials.

As shown in the presented Figure 4 and Figure 5 and in Table 1, as the sole stiffness increases, the peak flexion angle of the MTP joint decreases.

Moreover, despite the fact that this is only a preliminary analysis involving a small number of types of shoes and subjects tested, in the treadmill walking trials and in the stair climbing ones the relation found between sole stiffness and peak MTP angle could be described as linear ($R^2$ > 0.89) (Figure 4 and Figure 5). This fact is notable, due to the high complexity of the biological structures that are involved in the gait gesture. This means that, if this correlation is proven to be consistent in future research, it could be possible to estimate the peak MTP angle from the sole stiffness, and vice-versa.

Another remarkable result is that the difference between the slopes of the linear regression curves belonging to different walking conditions is not statistically significant within the same test session, meaning that a unique regression line can be computed for each test session. The consistency of this behavior will be investigated in future tests.

The main limitations of this study are the choice of focusing only on the sagittal plane, in which most of the MTP joint action takes place, the number of types of shoes examined and the number of subjects employed.

5. Conclusions

The aim of this research was to analyze the influence of shoe sole stiffness and terrain slope on the kinematics of the MTP joint angle.

The outcomes of this study proved that significant correlations exist between the above-mentioned quantities, and furthermore, with confirmation from further testing, it could be possible to estimate the peak MTP angle reached during gait by knowing the sole stiffness $K_{Fs10}^{MTP}$, when measured as described above.

As mentioned, since this preliminary study has some major limitations, future works will focus on increasing the number of types of shoes and subjects employed, to strengthen (or weaken) the consistency of the correlation found by augmenting the population and the amplitude of the statistics.