Introduction of 1-m MSBS in Tohoku University, New Device for Aerodynamics Measurements of the Sports Equipment †
Abstract
:1. Introduction
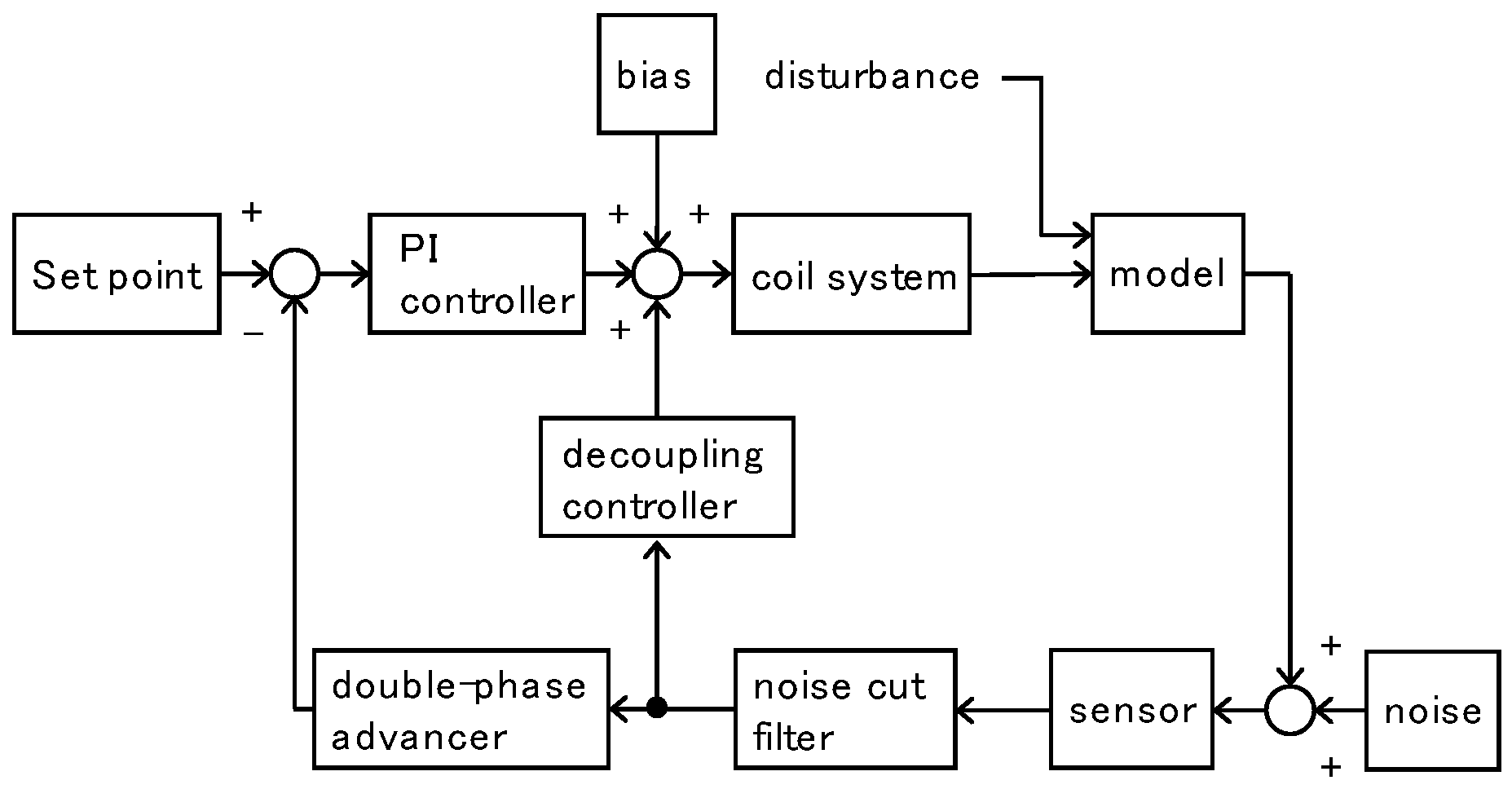
2. MSBS Principle
3. Outline of 1-m MSBS
4. Measurement of Sphere Drag using 1-m MSBS
4.1. Purpose of the Test
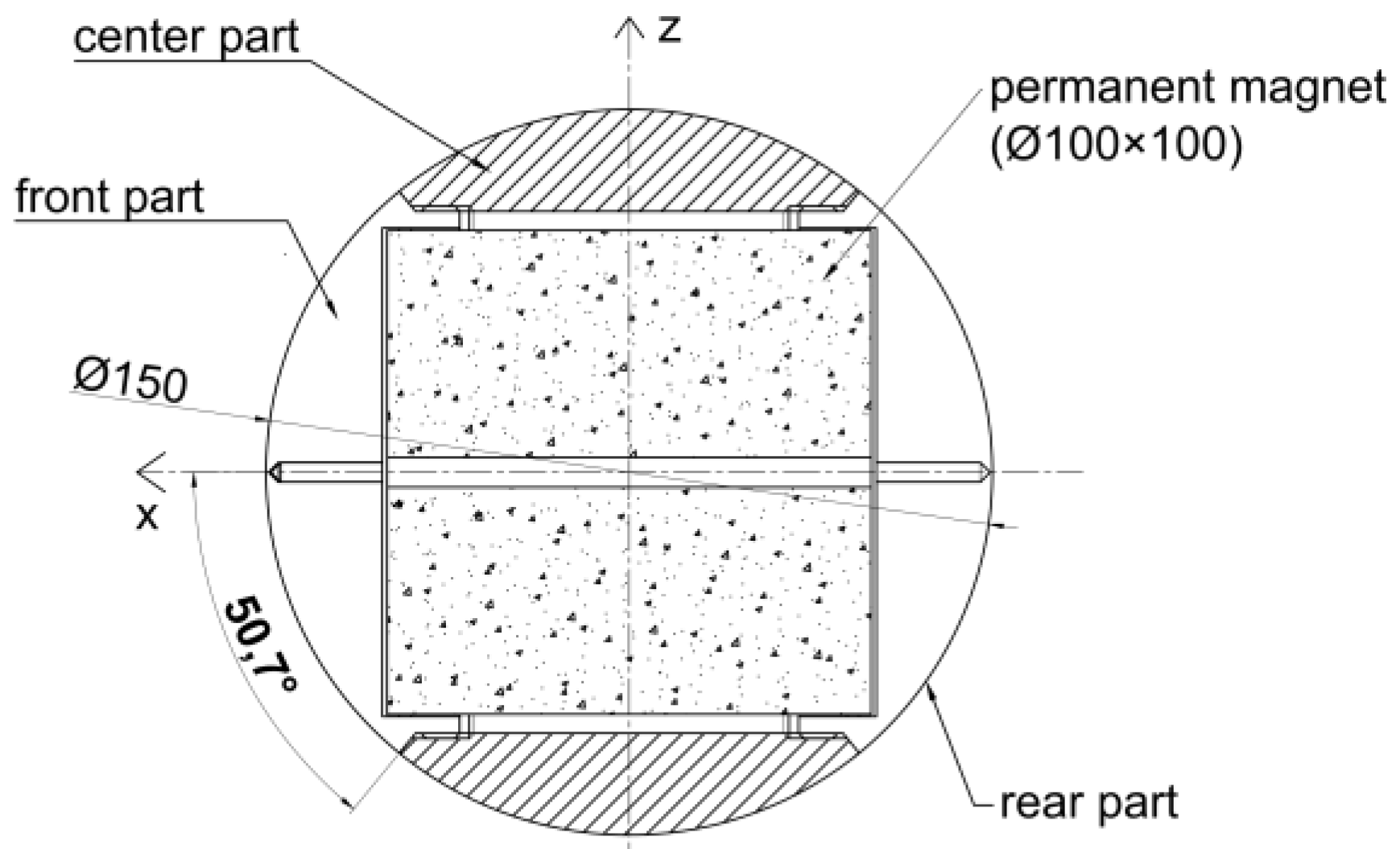
4.2. Apparatus and Model
4.3. Test Contents
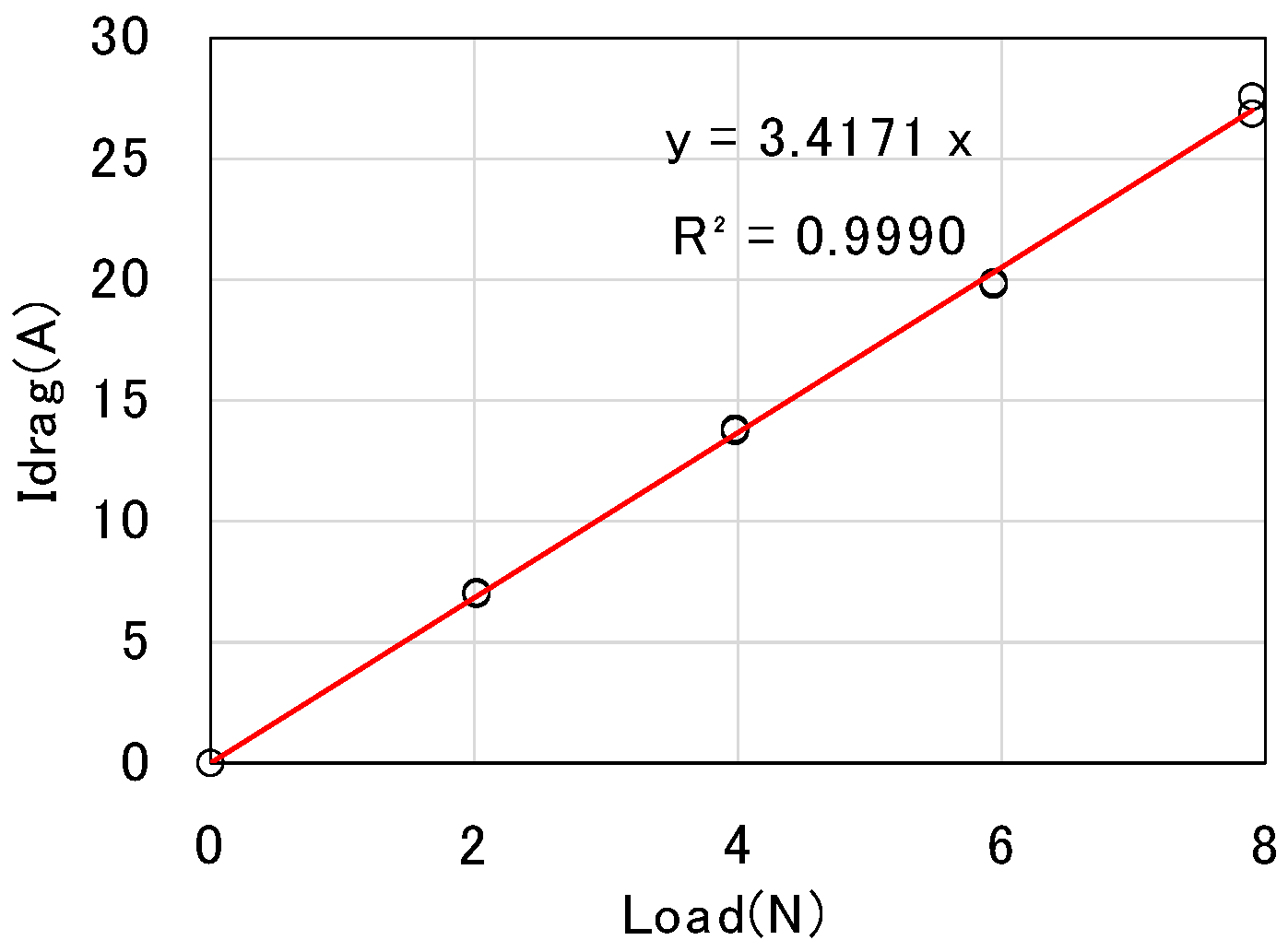
4.4. Results and Discussion
5. Concluding Remarks
Acknowledgments
References
- Hoerner, S. Tests of Spheres with Reference to Reynolds Number, Turbulence, and Surface Roughness; NACA-TM-777; National Advisory Committee for Aeronautics: Langley, VA, USA, 1935. [Google Scholar]
- Sawada, H. Wind Tunnels with Magnetic Suspension and Balance System. NAGARE 2014, 33, 267–272. (In Japanese) [Google Scholar]
- Kohama, Y.; Kobayashi, R.; Ito, H. Tohoku University Low-Turbulence Wind Tunnel. In Proceedings of the AIAA 17th Aerospace Ground Testing Conference, Nashville, TN, USA, 6–8 July 1992. [Google Scholar]
- Sawada, H. A Magnetic Suspension and Balance System for Wind Tunnels. Inst. Fluid Sci. Tohoku Univ. 2012, 24, 1–12. [Google Scholar]
- Sawada, H.; Suda, S. Study on aerodynamic force acting on a sphere with and without boundary layer trips around the critical Reynolds number with a magnetic suspension and balance system. Exp. Fluids 2011, 50, 271–284. [Google Scholar] [CrossRef]
- Taneda, S. Visual observations of the flow past a sphere at Reynolds numbers between 104 and 106. J. Fluid Mech. 1978, 85, 187–192. [Google Scholar] [CrossRef]



| Coil # | Coil Control Current | Function |
|---|---|---|
| 0, 9 | Idrag = (I0 + I9)/2 | Drag |
| 1, 3, 5, 7 | Ilift = (I1 + I3 + I5 + I7)/4 | Lift |
| Ipitch = (I1 + I3 − I5 − I7)/4 | Pitching Moment | |
| Iroll = (I1 − I3 − I5 + I7)/4 | Rolling Moment | |
| 2, 4, 6, 8 | Iside = (I2 + I4 + I6 + I8)/4 | Side Force |
| Iyaw = (I2 + I4 − I6 − I8)/4 | Yawing Moment | |
| Iroll = (I2 − I4 − I6 + I8)/4 | Rolling Moment |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Okuizumi, H.; Sawada, H.; Nagaike, H.; Konishi, Y.; Obayashi, S. Introduction of 1-m MSBS in Tohoku University, New Device for Aerodynamics Measurements of the Sports Equipment. Proceedings 2018, 2, 273. https://doi.org/10.3390/proceedings2060273
Okuizumi H, Sawada H, Nagaike H, Konishi Y, Obayashi S. Introduction of 1-m MSBS in Tohoku University, New Device for Aerodynamics Measurements of the Sports Equipment. Proceedings. 2018; 2(6):273. https://doi.org/10.3390/proceedings2060273
Chicago/Turabian StyleOkuizumi, Hiroyuki, Hideo Sawada, Hayato Nagaike, Yasufumi Konishi, and Shigeru Obayashi. 2018. "Introduction of 1-m MSBS in Tohoku University, New Device for Aerodynamics Measurements of the Sports Equipment" Proceedings 2, no. 6: 273. https://doi.org/10.3390/proceedings2060273
APA StyleOkuizumi, H., Sawada, H., Nagaike, H., Konishi, Y., & Obayashi, S. (2018). Introduction of 1-m MSBS in Tohoku University, New Device for Aerodynamics Measurements of the Sports Equipment. Proceedings, 2(6), 273. https://doi.org/10.3390/proceedings2060273






