Simulation of Mechanical Characteristics of Tennis Racket String Bed Considering String Pattern ^†

Abstract

The effect of string pattern on the mechanical characteristics of a tennis racket were simulated numerically. A numerical simulation program to evaluate deformation of the string bed of a tennis racket was developed using the finite element method. The formulation of a numerical simulation code is described in this paper. The applicability of the developed simulation program was investigated by comparing experimental results of loading tests on string bed specimens, for which the distance between strings was 12 mm. The out-of-plane stiffness and sliding characteristics of strings of an actual racket were simulated using the developed simulation code.

1. Introduction

The performance and feeling of tennis rackets are realized by the combination of the racket’s frame and string bed. Tennis players select their own individual tennis racket frame and strings depending on their play style and playabilities, individually. Currently, natural guts, nylon, polyester-strings and hybrid strings are available for tennis racket. Diameters of the strings have ranged from 1.2 mm to 1.35 mm since the 19th century. With the exception of missed shots, mechanical contributions are applied to the tennis ball by the string bed of a tennis racket. The stiffness of the string bed in the out-of-plane direction affects the speed of the impacted ball. The sliding characteristics of strings in-plane affect to the spin of the ball. So, the number of cross and main strings and the length and interval of each string are important engineering issues when designing a tennis rackets.

The effect of string bed properties on ball spin was investigated in recent researches [1,2,3,4,5,6]. Allen et al. (2010) showed that reducing ball/string friction can increase rebound spin by a computational model [1]. Haake et al. (2012) showed that rebound spin was dependent on inter-string friction experimentally [5]. Nicolaides et al. (2013) investigated the effect of string bed pattern on ball spin [6]. In these researches, they found that rebound spin decreased with the number of cross strings. Washida et al. (2014) showed measured data about relationships between number of cross strings and rebound spin [7].

In this paper, an original numerical simulation program of finite element method for string bed in tennis rackets are described. The simulation program was coded by the Fortran Language in UNIX system. For numerical modeling, simple beam elements which represent tensile load were applied to the modeling of orthogonal main and cross strings. Nominal force at each intersection of strings was calculated and the Coulomb friction model was applied with an elastic-plastic constitutive model to represent the in-plane slide of strings. The validity of the developed code is investigated through comparison with the experimental results of string beds in rectangular aluminum jigs. Simulated results of a tennis racket are shown to represent the applicability of the developed code.

2. Materials and Methods

The 3-dimensional Cartesian coordinate system was applied to string beds in this study. The positional relationship of the coordinates is shown in Figure 1. In preparation for the computational simulation, nodes for finite element analysis were prepared at all intersections of the main and cross strings. Also, additional nodes were prepared at grommets and their displacement was constrained. Beam elements (In Figure 2) are applied between nodes to represent the tennis strings. Tension of cross and main strings $T_x^{}$ and and $T_y^{}$ were assumed to be constant in this study. Forces at i^th and j^th nodes in z-direction are given by following equations:

$$f_z^{\left(i\right)}=\alpha \frac{T}{{\overline{L}}^{\left(i,j\right)}}\left(u_z^{\left(i\right)}-u_z^{\left(j\right)}\right), f_z^{\left(j\right)}=\alpha \frac{T}{{\overline{L}}^{\left(i,j\right)}}\left(u_z^{\left(j\right)}-u_z^{\left(i\right)}\right)$$

(1)

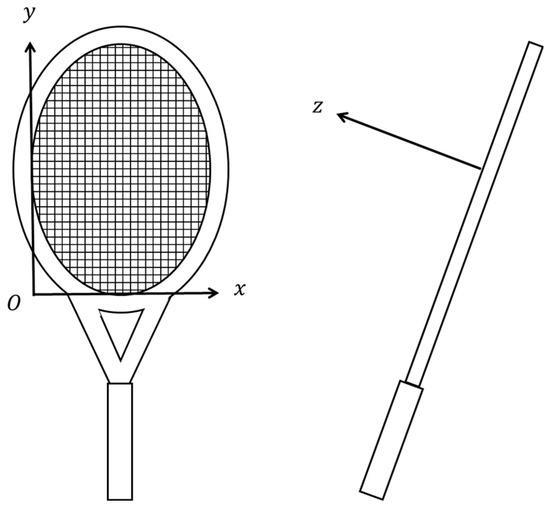
Figure 1. Coordination system for this research.

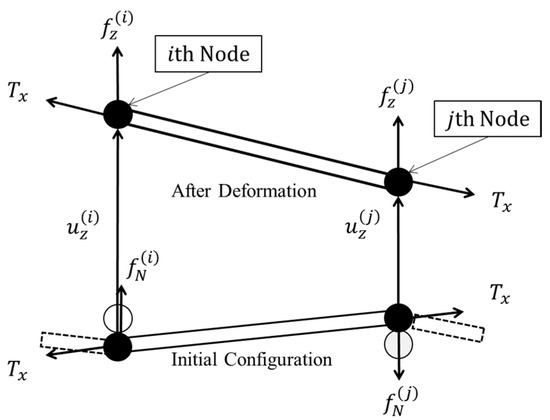
Figure 2. Deformation of string element in out-of-plane direction of string bed.

Here, i and j indicate respective node numbers. $u_z^{\left(i\right)}$ is displacement in the z direction of the i^th node. $T$ in Equation (1) corresponds to $T_x$ for horizontal strings and $T_y$ for vertical strings. ${\overline{L}}^{\left(i,j\right)}$ is the length between i^th and j^th nodes, which was updated at every step of the simulation. Length of strings ${\overline{L}}^{\left(i,j\right)}$ was calculated with ${\overline{L}}^{\left(i,j\right)}=L^{\left(i,j\right)}-u_x^{\left(i\right)}+u_x^{\left(j\right)}$ for cross strings and ${\overline{L}}^{\left(i,j\right)}=L^{\left(i,j\right)}-u_y^{\left(i\right)}+u_y^{\left(j\right)}$ for main strings. $\alpha$ is the adjusting coefficient of out-of-plane stiffness. The coefficient $\alpha$ is provided because there are strings that contribute to the out-of-plane stiffness and strings that do not. In Figure 2, it can be seen that strings at the intersecting points of the main and cross strings were located above or below the other strings. It is suggested that the strings at the j^th node did not make a strong contribution to out-of-plane stiffness because they were compressed when vertical downward force was applied to the j^th node. Conversely, strings at the i^th node made a strong contribution to out-of-plane stiffness because they stretched when vertical downward force was applied to the i^th node.

For the elements of cross strings, force at the i^th and j^th nodes in the x-direction (orthogonal to the string) were formulated with the following equations:

$$f_x^{\left(i\right)}=f_N^{\left(i\right)}\left(u_x^{\left(i\right)}\right)-f_N^{\left(j\right)}\left(u_x^{\left(j\right)}\right), f_x^{\left(j\right)}=f_N^{\left(j\right)}\left(u_x^{\left(j\right)}\right)-f_N^{\left(i\right)}\left(u_x^{\left(i\right)}\right)$$

(2)

The positional relationship of nodes, forces and displacement are shown in Figure 3. $u_x^{\left(i\right)}$ is displacement in the x-direction of the i^th node. $f_N^{\left(i\right)}$ is frictional force at the i^th node, which equilibrates with external force under the maximum frictional force. $f_N^{\left(i\right)}$ is defined as a function of the horizontal displacement of the i^th intersection of strings.

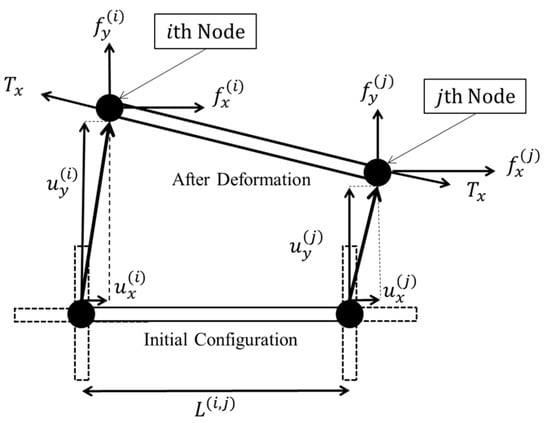
Figure 3. Deformation of string element with plane direction of string bed (Elements for main string).

Force at the i^th and j^th nodes in y-direction are formulated with the following equations considering the angular change of a string with constant tension $T_x$.

$$f_y^{\left(i\right)}=\frac{T_x}{{\overline{L}}^{\left(i,j\right)}}\left(u_y^{\left(i\right)}-u_y^{\left(j\right)}\right), f_y^{\left(j\right)}=\frac{T_x}{{\overline{L}}^{\left(i,j\right)}}\left(u_y^{\left(j\right)}-u_y^{\left(i\right)}\right)$$

(3)

Here, $u_y^{\left(i\right)}$ is the displacement in the y-direction of the i^th node. When seeking $f_x^{\left(i\right)}$, $f_y^{\left(i\right)}$ and $f_z^{\left(i\right)}$ of main strings, Equation (1) can be applied for $f_z^{\left(i\right)}$ of main strings. For in-plane stiffness, Equations (2) and (3) can be applied for $f_x^{\left(i\right)}$ and $f_y^{\left(i\right)}$ of main strings by exchanging the subscripts $x$ and $y$ representing direction. Here, $f_N^{max\left(i\right)}$ is the maximum frictional force of the i^th node. $f_N^{max\left(i\right)}$ was calculated as

$$f_N^{max\left(i\right)}=\mu f_N^{\left(i\right)}$$

(4)

where $\mu$ is the frictional coefficient and $f_N^{\left(i\right)}$ is normal force at the i^th node. $f_N^{\left(i\right)}$ was calculated from the initial configuration of the string bed as follows:

$$f_N^{\left(i\right)}=\frac{D}{2}\left(\frac{T_x}{L^{\left(i,k\right)}}+\frac{T_x}{L^{\left(i,l\right)}}\right)+\frac{D}{2}\left(\frac{T_y}{L^{\left(i,m\right)}}+\frac{T_y}{L^{\left(i,n\right)}}\right)$$

(5)

Here, $D$ is the diameter of the strings. String intersections did not slide easily when diameter $D$ was large. Positional relationships of the nodes in Equation (5) are shown in Figure 4. In this study, maximum frictional force $f_N^{max\left(i\right)}$ was calculated at all nodes of intersecting strings and assumed to be constant. For the simulation algorithm, an incremental calculation method was applied. Equations (1)–(3) were rewritten as incremental, as follows:

$$\Delta f_z^{\left(i\right)}=K_z^{\left(i\right)}\Delta u_z^{\left(i\right)}-K_z^{\left(j\right)}\Delta u_z^{\left(j\right)}, \Delta f_z^{\left(j\right)}=K_z^{\left(j\right)}\Delta u_z^{\left(j\right)}-K_z^{\left(i\right)}\Delta u_z^{\left(i\right)}$$

(6)

$$\Delta f_y^{\left(i\right)}=K_y^{\left(i\right)}\Delta u_y^{\left(i\right)}-K_y^{\left(j\right)}\Delta u_y^{\left(j\right)}, \Delta f_y^{\left(j\right)}=K_y^{\left(j\right)}\Delta u_y^{\left(j\right)}-K_y^{\left(i\right)}\Delta u_y^{\left(i\right)}$$

(7)

$$\Delta f_x^{\left(i\right)}=K_x^{\left(i\right)}\Delta u_x^{\left(i\right)}-K_x^{\left(j\right)}\Delta u_x^{\left(j\right)}, \Delta f_x^{\left(j\right)}=K_x^{\left(j\right)}\Delta u_x^{\left(j\right)}-K_x^{\left(i\right)}\Delta u_x^{\left(i\right)}$$

(8)

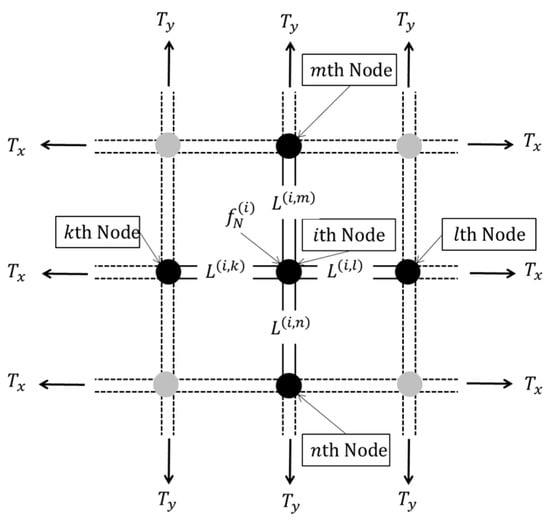
Figure 4. Positional relationships of nodes to calculate normal forces at cross-points of strings.

For cross strings, $K_z^{\left(i\right)}$ and $K_z^{\left(j\right)}$ are equal to $\alpha T_x/{\overline{L}}^{\left(i,j\right)}$. $K_y^{\left(i\right)}$ and $K_y^{\left(j\right)}$ are equal to $T_x/{\overline{L}}^{\left(i,j\right)}$. $K_x^{\left(i\right)}$ was defined as follows:

$$K_x^{\left(i\right)}=\frac{f_N^{max\left(i\right)}}{0.2} if \left(u_x^{\left(i\right)}\leqq 0.2\right),K_x^{\left(i\right)}=\frac{f_N^{max\left(i\right)}}{100} if \left(u_x^{\left(i\right)}>0.2\right)$$

(9)

In this study, elastic-plastic relation shown in Figure 5 was applied for modeling of friction.

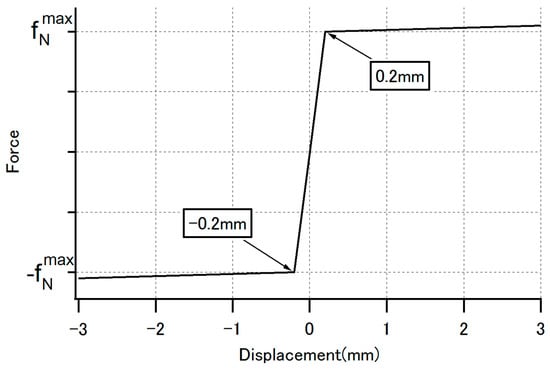
Figure 5. Relationship between friction force and displacement for intersections of main and cross strings.

3. Results and Discussion

3.1. Effect of String Pattern on Mechanical Characteristics of String Bed

To investigate the effect of string pattern on the mechanical characteristics of the string bed of a tennis racket, square string-bed specimens were prepared for which the interval of both vertical and horizontal strings was 12 mm. The string-bed specimen shown in Figure 6 was made with an aluminum outer frame with 16 string holes in each side. Loading tests of string-bed specimens to evaluate out-of-plane stiffness were conducted to investigate the effect of loading position and string tension on the out-of-plane stiffness of the string bed. Displacement distribution for numerical simulations is shown in Figure 7. Results of numerical simulation and loading tests are shown in Figure 8 and Figure 9. The effects of loading position and string tension on out-of-plane stiffness of a string-bed specimen were predicted well with numerical simulation. In this simulation, the coefficient $\alpha$ was assumed to be 0.6.

Figure 6. String-bed specimen; string interval is 12 mm.

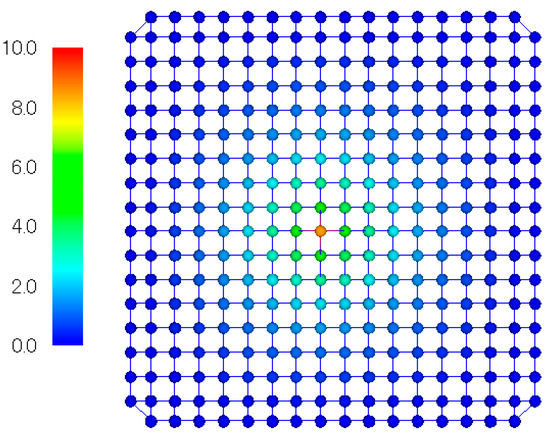
Figure 7. Simulated results of deformation of string bed at point A (force = 100 N).

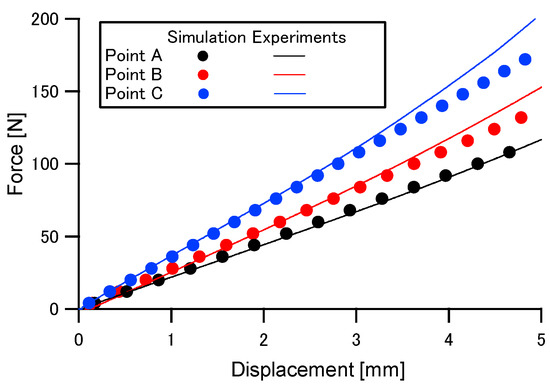
Figure 8. Relationships between displacement and force in out-of-plane direction.

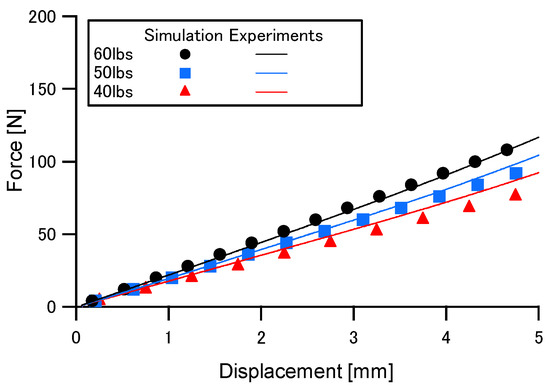
Figure 9. Effect of string tension on stiffness in out-of-plane direction.

3.2. Numerical Simulation of Mechanical Characteristics of Tennis Racket String Bed

Numerical simulations were conducted for a tennis racket (shown in Figure 10) to evaluate the out-of-plane stiffness and the in-plane slip effect of intersections. The out-of-plane stiffness of the tennis racket string bed and the sliding intersections of main and cross strings were calculated using the proposed method. Tennis ball load was assumed to be diagonal at 30 degrees in the x-z plane at the center, bottom and top points of the string bed, respectively. The geometric shape was measured on the actual racket. The frictional coefficient $\mu$ between the main and the cross strings was assumed to be 0.2. In Figure 11, the calculated distributions of the displacements of the tennis racket string bed are shown. Depending on the vertical position of the racket, there were no large differences in the distribution of the deformation in the out-of-plane direction. In Figure 12, displacement of the intersections in the in-plane direction are shown. The load at the red intersections was greater than the maximum frictional force $f_N^{max\left(i\right)}$, and this indicates that the intersections slid. In Figure 13, the relationships between displacement and force in the out-of-plane direction are shown. The out-of-plane stiffness of the simulated racket was not affected by the vertical position of the string bed. The effect of string diameter on sliding when loading to the center point is shown in Figure 14. Because strings with small diameters can easily slide laterally, it is expected that spin performance of actual rackets will be enhanced with the use of thin strings.

Figure 10. Tennis racket for simulation.

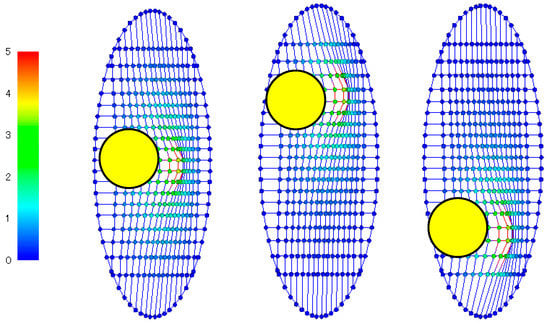
Figure 11. Simulated results of deformation of string bed in tennis racket (force=100 N, display 10 times displacement in out-of-plane direction).

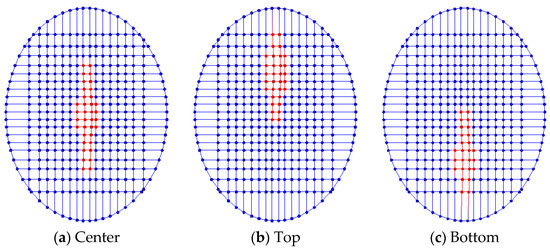
Figure 12. Simulated results of sliding intersections of tennis racket (intersections that slid ware shown as red circles, non-sliding intersections are shown as blue circles).

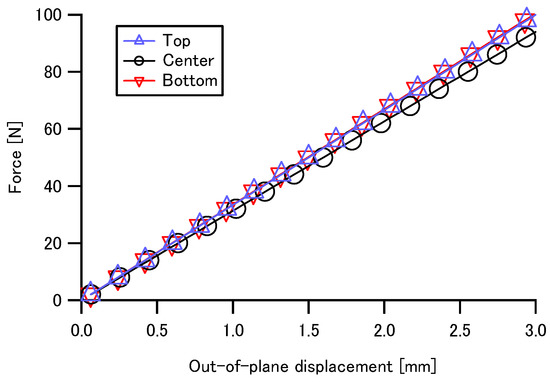
Figure 13. Effect of loading position on out-of-plane stiffness.

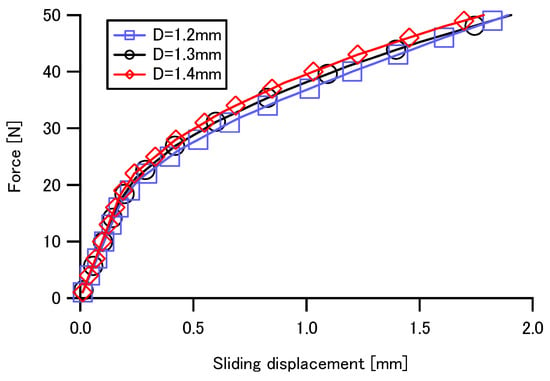
Figure 14. Effect of string diameter on sliding of intersections.

4. Conclusions

In order to construct a design method using a numerical analysis of racket performance, we modeled the tennis racket string bed using a finite element method. String-bed specimens were prepared, and the applicability of our proposed method was confirmed by comparing the numerical simulations with experimental data. It was possible to predict the distribution of the out-of-plane stiffness and slip performance of the actual racket strings using this simulation method.