1. Introduction
The Wimbledon Championships is the oldest tennis tournament, the first being in 1877, three years after the “invention” of lawn tennis by Wingfield [
1]. In 1874 Wingfield patented the game [
1] and started marketing kits for playing. Racket developments were incremental for almost one hundred years [
2], but major changes started in the 1970s when Head pioneered a new design with an ‘oversized’ racket head [
3] and engineers started to employ new materials [
2,
4]. The game has changed considerably over time, partly due to changes in the racket. Indeed, the maximum speed that a player can swing a racket is thought to decrease as its Transverse Moment of Inertia (MOI) increases [
5,
6], indicating that modern lightweight designs can be swung faster. Haake et al. [
2] predicted that a player could serve 18% faster with modern equipment compared to what was available in 1870s, mainly due to this increase in swing speed. Innovations in racket design, prompted the International Tennis Federation (ITF) to limit some parameters (e.g., max. length/width), yet the rules still allow variability in stiffness, inertia and string bed properties, which all influence aspects of racket performance.
Engineers, designers and biomechanists undertake research to further our understanding of racket performance [
7], with attention paid to issues such as the factors affecting frame vibrations [
8] and swing speed [
5,
6]. Haake et al. [
2] represents the most comprehensive work on how rackets have developed to date, having characterised 150 from the 1870s to 2007, including measurements of overall length, head length/width, grip length, mass, centre of mass (COM), “swing-weight”, “twist-weight” and vibration frequency. This paper lays the foundations for future research, by piloting protocols on one hundred rackets, and making recommendations for succinctly characterising a much larger number in the future, while also measuring more properties.
2. Materials and Methods
Ninety-one rackets were characterised at a brand’s headquarters. There were over one thousand rackets in their collection, spanning a range of brands and eras. Rackets were selected from different brands and eras (e.g., Dunlop Maxply Fort, Prince Pro, Yonex R22, Wilson Pro Staff, HEAD Radical, Babolat Pure Drive), including those which were distinctive (e.g., Gamma Big Bubba—Xtra long 32″, Kuebler Original Widebody 280 Hz, Snauwaert graphite ergonom) to thoroughly assess the robustness of the protocols. Nine rackets came from the University. Only strung rackets were selected. For each racket, manufacturer details and key measurements were recorded (
Table 1), a photograph was taken, and any distinguishing features were photographed and documented.
Modal analysis was used to determine the frequency of the first bending mode. The racket was suspended with string and a sensor (MetaWear CPro, Mbientlab Inc., San Francisco, CA, USA) was strapped to the handle (8 g sensor & strap). The string bed was ‘tapped’ with a ball to excite vibrations, with the accelerometer sampling at 800 Hz (BMI160 inertial measurement unit, Bosch Sensortec, Reutlingen, Germany). Data was logged in the sensor memory, transferred to an iPad via Bluetooth and downloaded (MetaWear App) to a laptop. The Fast Fourier Transform (FFT) function in Matlab R2106a (Mathworks) was applied to obtain the frequency. Tests were undertaken twice and the mean reported. The maximum difference between trials for a racket was 2 Hz (5 occurrences). Accuracy was assessed by fixing the sensor to a shaker and exciting frequencies of 100, 150 and 190 Hz, typical for tennis rackets [
2] and predictions fell within 2 Hz.
While devices are available for measuring Transverse MOI about an axis through the handle (‘swing-weight’) (e.g., Babolat Racquet Diagnostic Center, Prince Precision Tuning Center), this work trialed low-cost, portable techniques [
9]. A Simple Pendulum was used to obtain Transverse and Lateral MOI about the butt. A device (modified pipe with jubilee clip, 8.5 cm long & 40 g) was produced to attach a metal rod (0.8 cm diameter, 18 cm length) to the butt. Each end of the rod rested on an upturned angle iron (sides at 45° to horizontal), allowing the racket to swing. Bifilar Suspension was used for Polar MOI, with the racket hung from two 0.54 m strings, strapped (<1 g each) to the frame. For all tests, the time for 50 swings/oscillations was measured with a stopwatch to a resolution of 1 s. Tests were undertaken twice and the mean reported. The maximum difference between trials for a racket was 1 s for Transverse (twenty-one occurrences) and Lateral (twenty-eight occurrences) MOIs, equating to ~1.5% difference, and 2 s for Polar MOI (one occurrence), equating to ~5% difference.
Accuracy was assessed using two rods of known theoretical MOIs close to typical values for rackets. The Polar MOI of one rod was 0.00186 kg·m
2, and the Transverse MOI about the end of the other was 0.0576 kg·m
2. Three operators ran each test twice, resulting in a total of six for each MOI. Polar MOI was measured as 0.00190 kg·m
2 and Transverse MOI ranged from 0.0567 to 0.0577 kg·m
2 (mean value 0.0570 kg·m
2), indicating similar agreement to theoretical values and the accuracy results reported by Spurr et al. [
9] (mean within 2%). Attempts were made to measure MOI with the sensor, by attaching it to the rods and then applying an FFT to the signal (accelerometer & gyroscope) to predict the frequency of oscillation, but initial results indicated that this was less accurate and more time-consuming than using the stopwatch.
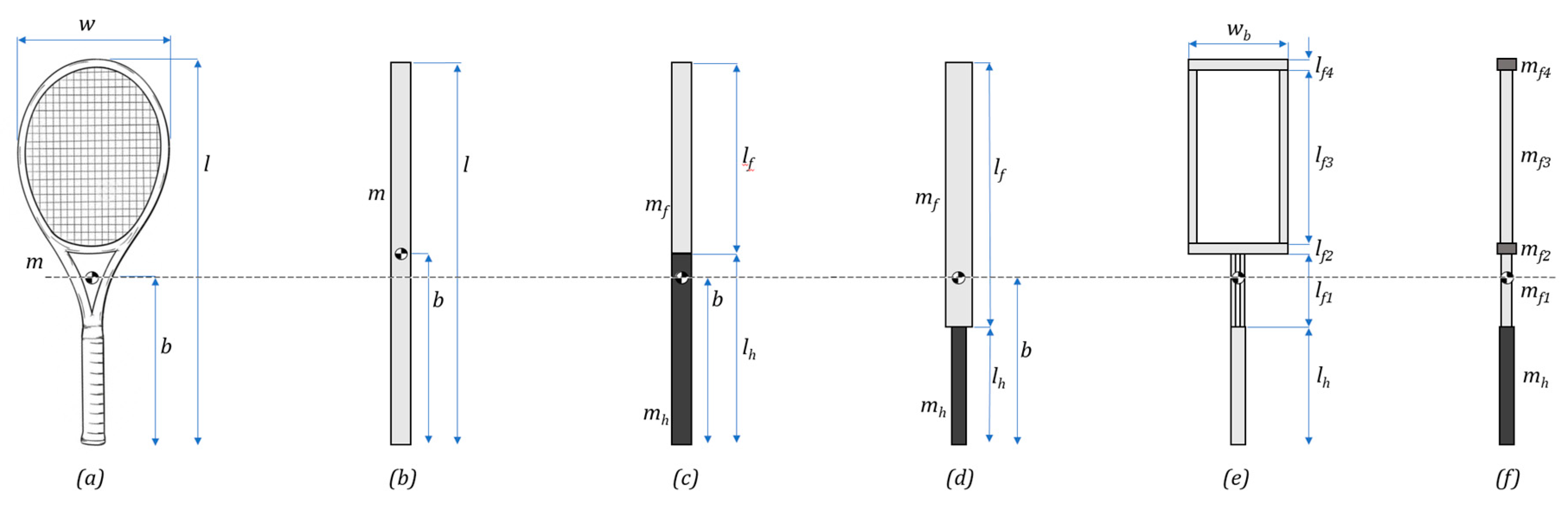
As well as measuring the Transverse MOI (I
T) in our Pendulum technique, models were investigated to determine their suitability for predicting Transverse MOI from racket dimensions, mass and COM location [
10,
11]. The simplest approach is to model the racket as a beam [
10] (
Figure 1b).
Cross [
10] improved on the beam model, dividing the racket into two equal lengths, corresponding to the mass of the frame and handle (two-section beam;
Figure 1c):
As the mass of the sections sum to the racket mass, their values can be obtained using:
Goodwill [
11] divided the racket into two unequal lengths, corresponding to the mass and length of the fame and handle (unequal two-section beam;
Figure 1d):
Similarly, the mass of the sections can be obtained using:
Goodwill [
11] also developed a five-section beam model, which was shown to be more accurate than the two-section beam models for seven relatively modern rackets (
Figure 1e,f):
The five-section beam model starts with a two-dimensional approximation of a racket, with a rectangular head and two vertical throat sections (
Figure 1e). The width of the rectangle was set to 75% of the racket width. Translation to a one-dimensional beam can be obtained once section masses are known (
Figure 1f). In this work,
lf2 was assumed to equal
lf4 (from int. & ext. head length), so
mf2 equaled
mf4. As the mass of all sections sum to the racket mass, their values can be obtained using:
A Stepwise Linear Regression model was also conducted to examine the racket parameters that best predict the Transverse MOI; it was conducted on all dimension variables (lengths, widths, depths), as well as COM location and mass.
3. Results
Rackets were from twenty-seven manufacturers (36 HEAD, 8 Prince, 7 Wilson & Dunlop, 5 Babolat, 4 Kuebler & Volkl, 3 Yonex & Donnay, 2 Fischer, Neoxx, Rossignol, Slazenger & Techno, 1 Snauwaert, Wavex, Gamma, Huntak, Kneissel, Adidas, Montana, Prokennex, Alibor, Spinspot, Pottak, ATP & Life Sport). The majority were made of fibre-reinforced composites (85), followed by wood (8), metal (3) or a combination of different materials (e.g., fibre-reinforced wood) (4).
Table 2 summarises geometric properties and
Table 3 summarises inertial properties, string bed properties and frequency of the first bending mode. Distinguishing features included holes in the frame (Prince Ozone 7), extended string bed/no throat section (Alibor TX 9980), asymmetric frames (Snauwaert graphite ergonom), adjustable string bed patterns (HEAD Extreme Rev Pro) and unusual throat sections (Rossignol F200 Wilander).
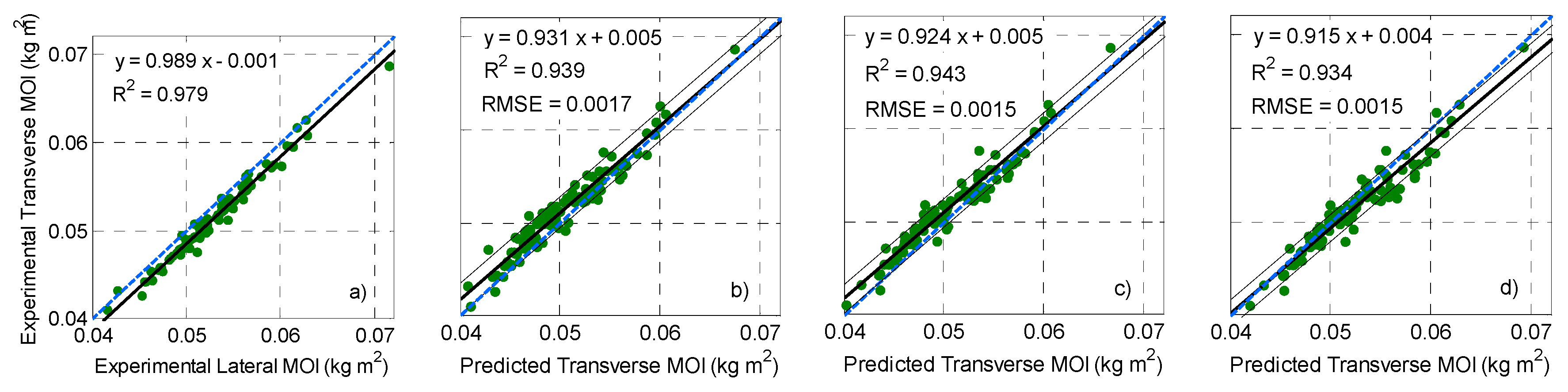
Figure 2a shows experimental Transverse versus Lateral MOI. It was not possible to measure Transverse MOI for two asymmetric rackets (Neoxx, ET 320 Pro and ST 285), so these were excluded. The MOIs were well correlated as the correlation coefficient,
R, was very close to 1. Lateral MOI was slightly higher, as evidenced by an intercept of −0.001 kg m
2.
Figure 2b–d shows that Transverse MOI was predicted well by all the models. All models were well correlated with the data (all R
2 > 0.934), with trendline gradients close to 1, and low intercept and root mean squared error (RMSE) values (
Figure 2b–d). When a threshold of ±5% was introduced, fifteen rackets were out of this range for the two-section beam, reducing to twelve for the five-section beam (three of them being made of wood out of a total of eight wooden rackets) and only five (included in the fifteen of the two-section beam) for the unequal two-section beam. The maximum error was 9.5% for the two-section beam, 7.4% for the unequal two-section beam and 7.7% for the five-section beam. When the threshold was decreased to ±3%, the five-section beam was still consistent for seventy-five rackets, against sixty-five for the unequal-two section beam and only fifty-nine for the two-section beam. The Stepwise Linear Regression model indicated that mass (partial correlation (pC) = 0.941), COM location (pC = 0.864), racket length (pC = 0.492), and head width (pC = 0.245) all significantly contributed to Transverse MOI (R
2 = 0.936,
p < 0.001), although removing head width did not have much of an effect on the model overall (R
2 = 0.930,
p < 0.001).
4. Discussion
The properties of one hundred rackets, from twenty-seven manufacturers and different eras, were characterized using low-cost techniques; overall properties were close to previously reported values (e.g., [
2,
9,
10,
11,
12]), although not all of these parameters (e.g., frame depth, no. of strings) have been well documented previously for so many rackets. The information presented here provides typical racket values and ranges, which could be useful for predicting performance using models.
Manufacturer details and materials data—were sometimes stated on a tag or text graphic (e.g., graphite) or estimated from visual inspection (e.g., wood, aluminum), but future work should consider the level of confidence in this information. In a similar manner, it was not feasible to identify string materials from visual inspection. Moreover, as strings can be replaced documenting their properties—material and diameter—is not recommended in future work. The same applies for measuring handle circumference, as grips vary, degrade and may not be original. The minimum value of frame depth often corresponded to the throat section. Future work could document the maximum and minimum depth of the frame and throat. Distinguishing features often fell into categories, such as asymmetric geometry, unusual head shapes, unusual throat sections or holes in the frame. Future work could document these features within categories, to save time and facilitate analysis, only including descriptions for particularly distinctive rackets.
Modal analysis with the wireless sensor was fairly time-consuming and future work could explore options to streamline the process, such as using a wired accelerometer. The range in vibration frequency was relatively small, with many rackets having similar values. Differences were, however, observed by the operator in how rackets damped frame vibrations. For some rackets, the lowest frequency did not correspond to the out of plane bending mode, rather it was the in plane bending mode (e.g., Kuebler Original Widebody 280 Hz, which had a max frame depth of 33 mm). Future work could document the frequency of both in plane and out of plane bending modes, as well as investigating damping coefficients.
Measurements of MOI were particularly time consuming, taking around ~30 to ~80 s for 50 oscillations. As Transverse and Lateral MOI were highly correlated [
12], it may not be strictly necessary to measure both when characterizing a large number of rackets. It is also possible to predict Transverse MOI reasonably well using a two-section, unequal two-section or five-section beam model. The accuracy of the three models for predicting Transverse MOI was similar, so the unequal two-section beam model may be preferable, due to its relative simplicity. Furthermore, the regression analysis indicated that, while including head width had a significant impact on Transverse MOI, overall, results were not very different when it was removed. Mass, COM location, racket length and head width were the best predictors of Transverse MOI, in that order. Mass, length and width are easy to measure accurately, however the accuracy in the measurement of COM location could be improved by using load cells. Future work could streamline the testing process by using a model to predict MOI. As some rackets had asymmetric heads, which is typical in vintage specimens [
2], further work should determine the suitably of the models for predicting Transverse MOI. Further work could also look to develop, or fine-tune, the models to increase accuracy of MOI predictions. More detailed modelling of key rackets, such as finite element analysis [
13], might give a greater understanding of performance parameters.