Study of Bio-Mimicry Surfaces for Optimization of Coupling Performance in Wheelchair Racing Gloves ^†

Abstract

In wheelchair racing, the optimal pair of gloves, as well as knowledge of conditioning of glove-rim contact surfaces can have a significant impact on race performance. Extreme temperatures, humidity, wet or dry conditions can considerably influence not only the hand-rim friction coupling (effectiveness of the athlete’s push cycle) but also the risk of injuries, blisters or sore areas which in turn, can influence the endurance of the athlete across long distance events. This paper reports an experimental study of the effect of bio-mimicry surface textures as a supplement for heightening glove-rim coupling for dry and wet weather conditions. The paper also provides recommendations for the practical implementation of the study findings through a proposal for the design and development of a pair of bespoke gloves for a wheelchair racing athlete for initial prototyping and performance trials.

1. Introduction

In wheelchair racing, forward propulsion is largely dependent on the friction that is created between the gloves and push rim as the wheels are in motion. The force exerted on the hand-rim by the wrist is best described by the radial, axial and tangential components of the resultant (total) force, where the friction component is primarily induced by the radial and axial force components to allow a tangential force component to be applied to the hand-rim [1]. The tangential force is the only force component that contributes to the forward motion of the wheel. Hence, slippage at the contact surface area will result in not only lost energy but also loses in athlete rhythm and thus non-optimal performance.

Racing gloves are made of a hard-thermoplastic core under the tradename of Aquaplast, subsequently covered by a 5 mm rubber sheet layer which is glued to the pushing surface to make the contact surface with the rim. During a race, the friction between the gloves and push-rim can be greatly affected by the weather conditions, the speed of the contact surfaces, as well as the design of the contact surface area of the glove. To overcome some of these sources of variation to friction is common practice amongst athletes to see the addition of tacky spray compounds such as Harpix Resin Klister to assist push effectiveness during wet weather condition for instance.

There are some studies in the literature looking at friction forces in relation to wheelchair propulsion. Xu et al. [2] investigated the influence of surface roughness of rubber on sliding friction for both, lubricated and dry conditions. This study showed that friction coefficient does change for varying contact speeds when rubber is in contact with a smooth surface. It is also shown that when the condition of the rubber is altered, such that a lubricant is added, the coefficient of friction is decreased [2]. Marcou et al. [3] studied flat and wedged glove surfaces for wet and dry conditions using a range of friction contact surfaces. Their findings recommended improving hard glove performance under wet condition by choosing wear resistant, high friction coefficient materials such as suede for the glove surface material, and/or by including a wedge in the design of the glove [3] which resulted in low stall positions. The study by Marcou et al. used similar testing conditions which can easily serve to draw conclusions on the racing application; typical testing values found in wheelchair racing range around 150–170 N for the contact force component, 5–10 m/s for testing speeds and a mean contact time with the wheel on the push phase of approx. 0.21–0.23 s [1,4,5].

With the aim of setting up a robust experimental design for this application with the potential for future use; this paper presents a study of the interaction between geometry, scale and conditioning of texture to explore potential effects on static and dynamic friction for glove performance.

The design of textures based on Biomimicry is used as a way to consolidate a clear example for the application. The octopus is well known for the suction pads that are present on their tentacles. The adhesion that is created to the surface through a suction pad is due to the negative pressure that can be created within the suction pad. As this adhesion isn’t purely dependent on an abrasive friction mechanism, this can limit the effect that a lubricant, or in an octopus’s case, water has on the magnitude of adhesion. The gecko is also well known for its ability to adhere to a majority of surfaces allowing it to maneuver large range of vertical surfaces and even on negative incline surfaces with high agility. Although most of the gecko’s adhesive ability is bound to the nanostructure of the setae in the gecko’s foot, which is comprised of nearly five hundred thousand keratinous hairs and potentially could be more closely replicated by a type of suede or microfiber texture. However, at the meso scale, the setal area is structured in a slight chevron style pattern. This type of macroscopic orientation and preloading of the seta has been found to increase attachment force above that of base material frictional measurements and to reduce the forces necessary to peel the gecko’s toe by detaching above a critical angle with the base [6].

The experimental design proposed in this paper will focus on studying the effect on static and dynamic friction due to the interaction of geometries such as suction pads and chevron textures at different scales and speeds for wet and dry conditions. The experimental design will be validated through an additional experiment including a tacky spray compound condition, which is known to increase dynamic friction and push effectiveness in wheelchair racing under wet weather conditions. It is intended that this experimental design will allow the future study of other relevant and readily available textures to wheelchair racing in the future.

2. Materials and Methods

2.1. Modelling and Fabrication of Specimens

Autodesk Fusion 360 software was used to design the texture constituents for three different friction surfaces; flat, chevron and suction pads. The two texture constituents (suction pads and chevron) were then scaled and patterned to produce testing specimens at a macro (100%), meso (50%) and micro (25%) scale. The scale assigned to both textures provided surface contact areas of 42.49, 10.62 and 2.66 mm² for macro, meso and micro respectively. The printed textures and geometries can be seen in Figure 1 below; chevron (Figure 1a,b) and suction pads (Figure 1c,d).

The specimens were 3D printed using an Objet500 Connex3 from Stratasys, with a printing resolution of 600 dpi; 30 um in the Z direction (height) and a 42 um in the X and Y directions of the print. The specimens were printed in a blend of 70% ‘Tango’ and 30% ‘Vero’ materials which result in a ‘rubber-like’ material pliable enough to be adapted onto complex surfaces and strong enough to ensure texture degradation on testing doesn’t occur due to material type. All surfaces were produced with a matte surface finish.

2.2. Experimental Protocol

Initially, a mixed-level fractional factorial design comprised of three 3-level design factors (A, B, C) and one 2-level design factor (D) as detailed in

Table 1. Mixed-level fractional factorial design table comprising three 3-level design factors (A, B, C) and one 2-level design factor (D).

Factor	Level 1	Level 2	Level 3
A: Texture type	Flat	Chevron	Suction Pads
B: Scale	Macro	Meso	Micro
C: Speed (mm/min)	120	800	1500
D: Conditioning	Dry	Wet	(Validation only = Tacky)

was proposed. A Taguchi L₉ experimental array was selected based on the number of design factors, and levels and the resultant experimental specimens are presented in

Table 2. μ_s and μ_k Results for both experimental designs—L₉ (2¹ x 3³) and L₉ (3⁴).

Experiment #	Factor A (Texture)	Factor B (Scale)	Factor C (Speed)	Factor D (Conditioning)	μs L9 (21 x 33) DOE	μk L9 (21 x 33) DOE	μs L9 (34) DOE	μk L9 (34) DOE
1	1	1	1	1	1.47	0.72
2	1	2	2	2	0.35	0.23
3	1	3	3	1(3)	1.46	0.70	(11.09)	(5.07)
4	2	1	2	2(3)	0.57	0.17	(4.71)	(2.13)
5	2	2	3	1	1.01	0.43
6	2	3	1	2	0.57	0.25
7	3	1	3	2	0.85	0.24
8	3	2	1	2(3)	0.69	0.20	(3.14)	(2.49)
9	3	3	2	1	2.39	1.61

(results section) Note that at the onset, factor D uses a random distribution of levels 1 and 2 through the L₉ array to compensate for lack of a third level. Subsequently, once the experimental trial of L₉ designs was completed (with factor D at two levels), experiments #3, 4 and 8 were repeated for validation using 3rd-level conditioning for Factor D (tacky spray).

Taguchi designs use ANOVA to analyze variance across factor levels. The minimum sample size required associated with the degrees of freedom (DOF) of factors and error from the F-table is 15. Hence, the L₉ array was performed twice to obtain statistical significance; this is induced by the one degree of freedom attached to the 2-level factor [7].

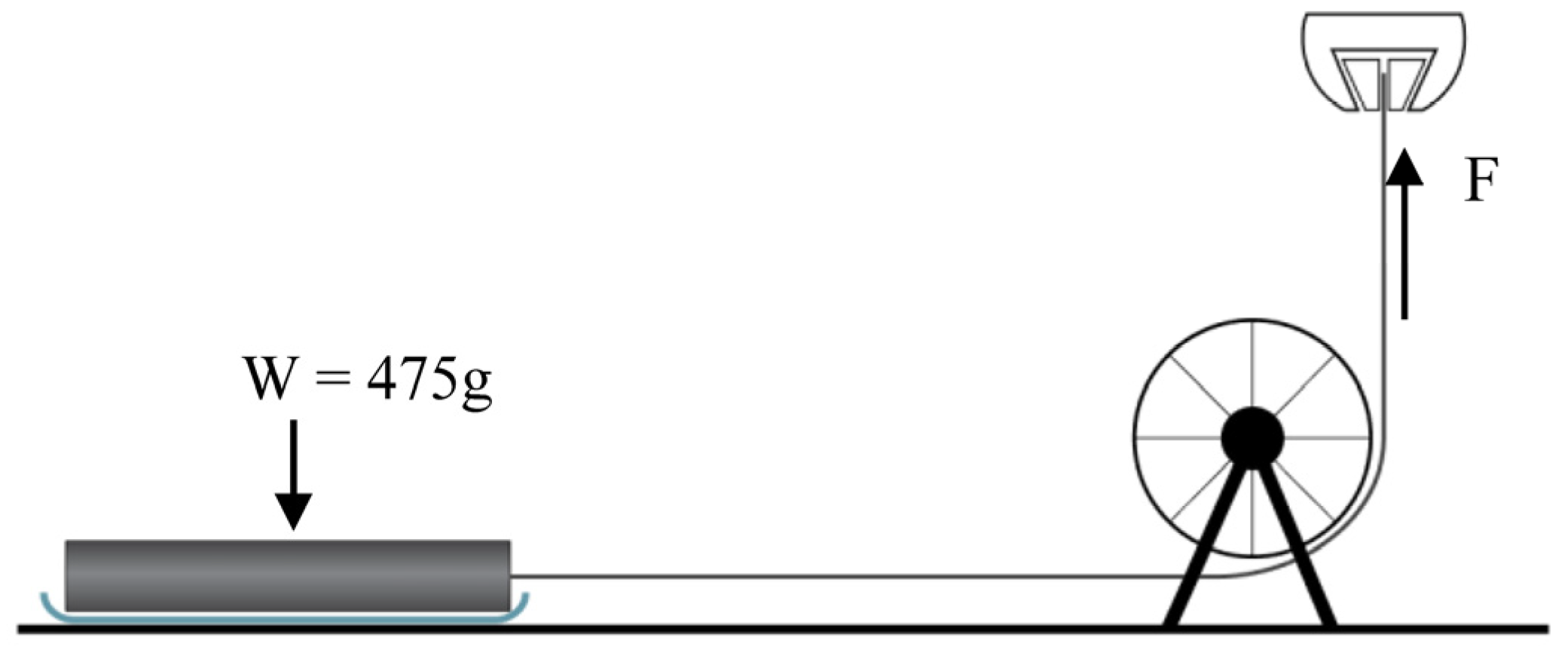
Each printed specimen was tested using the set up shown in Figure 2, which resulted from a modified interpretation of ASTM D1894-14. Using an Instron 5966 Dual Column testing system a sled was drawn; before each trial, the sled was pretension to 0.2 N, a sled weight of 475 g ($W$) was used. The test surface that was used was an Epoxy resin-Carbon Fibre composite. Load measurements were taken using the 10 kN load cell with the Bluehill 3 software. Load Measurements were taken at initial motion force. Subsequently, every 5 mm the sled travelled, an average of the load was taken to calculate the coefficient of friction. The speed was instantaneous, with no ramping of speed applied. For the dry condition, specimens were left to air dry after rinsing. The specimens were kept at room temperature and humidity, specimens did not experience any excessive heat or humidity.

The static and dynamic friction coefficients are given by Equations (1) and (2) respectively, where $A_s$. is initial maximum force reading; $W$ is the Normal force; and $A_k$ is average force.

$$u_s=\frac{A_s}{W}$$

(1)

$${\mu }_k=\frac{A_k}{W}$$

(2)

2.3. Data Analysis

Firstly, a graphical method for simple analysis of experimental data was used. This method involves plotting the mean values of the output (μ_s & μ_k) for each factor level. At this simple level of analysis, interaction effects between factors were mostly ignored, and only some basic idea of the effect of the level on the design was obtained, which was being used to reduce the number of variables or monitor the level trend effect for future experiments.

Subsequently, an ANOVA analysis was performed as the interest lays on knowing whether factors were significantly different in their measured behavior, or not. To analyze the F values in the ANOVA analysis critical F-values of 5.12 (N = 18, DOE = 9) and 4.46 (N = 18, DOE = 8) for L₉ (2¹ × 3³) and L₉ (3⁴) respectively. Additionally, a positive coefficient of correlation r was used for significant values at α = 0.05.

3. Results

Table 2 presents mean values of μ_s and μ_k for each of the nine experiments in the L₉ array as well as for validation experiments 3, 4 and 8.

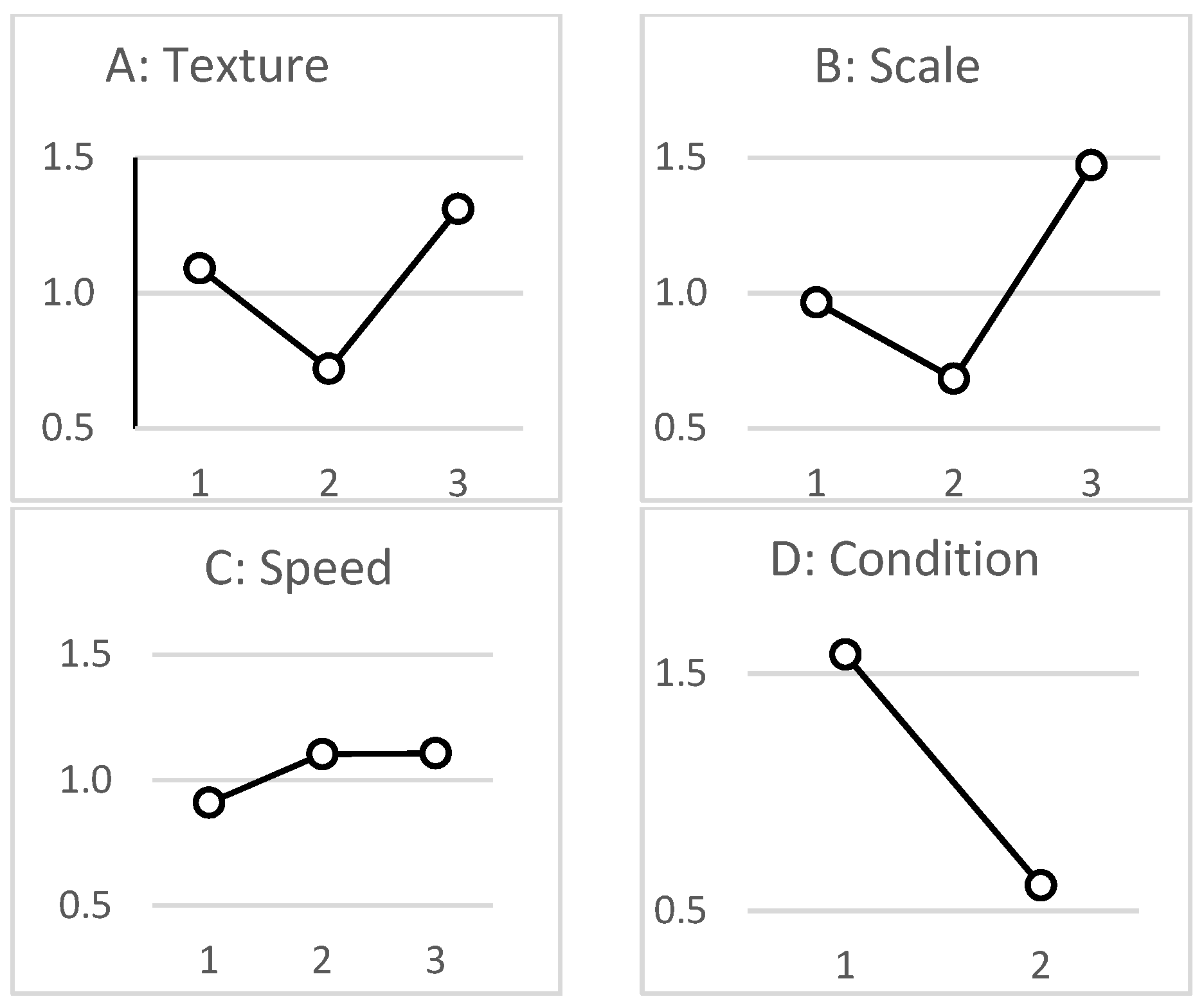
The plots shown in Figure 3 and Figure 4, present factor level effect on μ_s and μ_k respectively, for the mixed-level L₉ (2¹ × 3³). Subsequently,

Table 3. L₉ (2¹ × 3³) Sum of squares, variance, and F-values. F > 5.12 and (+sig) at α = 0.05.

Factor	μs				μk
	SS	Var	F-Value	sig	SS	Var	F-Value	sig
A	1.07	0.54	0.26	−0.18	0.48	0.24	0.50	−0.12
B	1.92	0.96	0.46	−0.09	1.12	0.56	1.15	0.06
C	0.15	0.08	0.04	−0.36	0.25	0.13	0.26	−0.22
D	4.20	4.20	2.01	0.10	1.86	1.86	3.84	0.21
SST	26.10				8.08
Error	18.76	2.08			4.37	0.49

presents the F-test values and significance of factor effect.

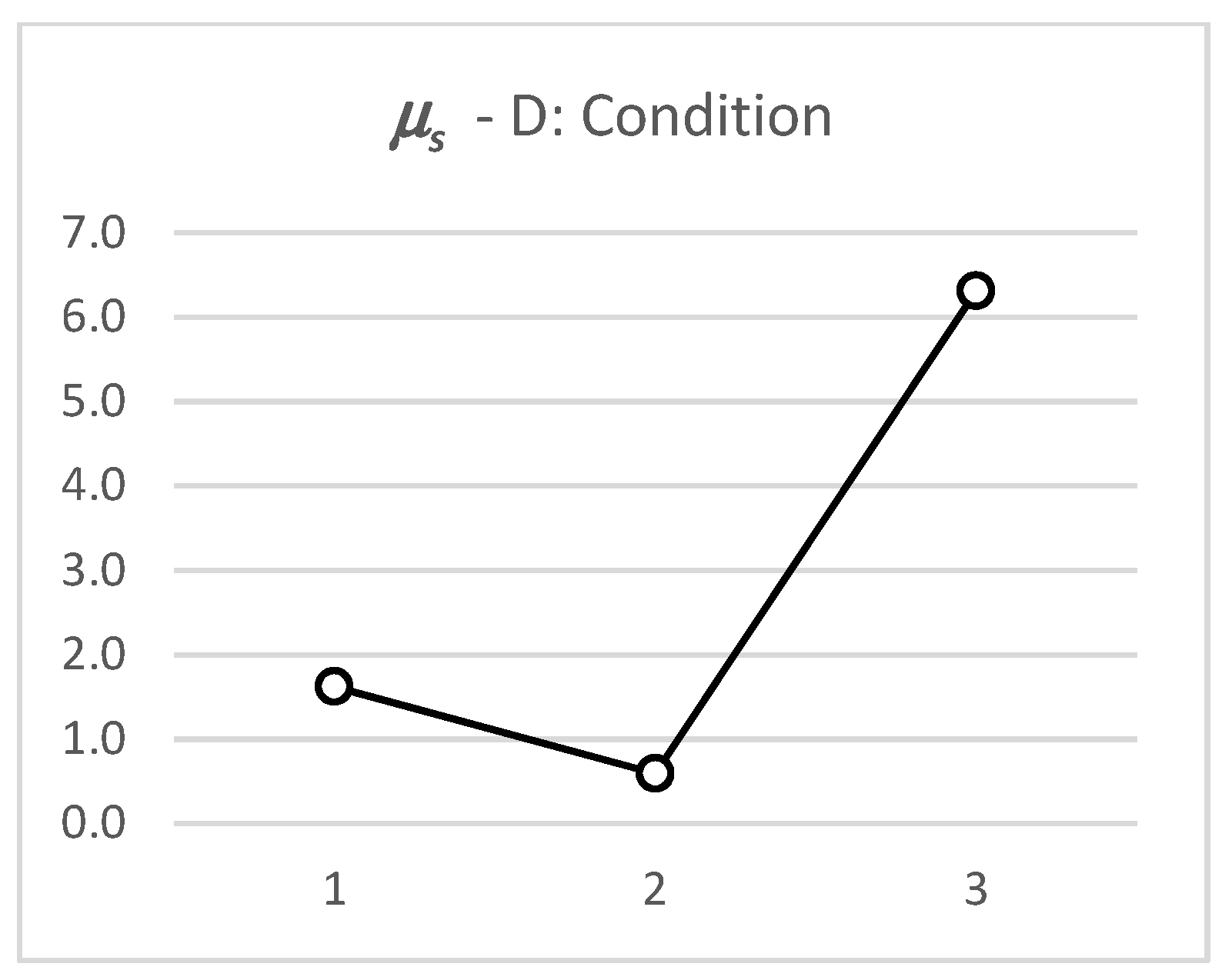
The plots shown in Figure 5 and Figure 6, present the level effect of conditioning (factor D) on μ_s and μ_k respectively, for the subsequent validation tests repeating experiment #3, 4 and 8 in L₉ (3⁴).

4. Discussion

When looking at level effect for geometry factors in Figure 3 and Figure 4, the suction pads at the micro scale presented a strong positive effect (however not significant) on both static and dynamic friction. This is also consistent with the dry condition with the highest values of μ_s and μ_k achieved across L₉ (2¹ × 3³) results.

F-values returned no significant effects for any of the factors at any Factor D conditions. However, from Table 3 and

Table 4. L₉ (3⁴)—Sum of squares, variance, and F-values. F > 4.46 and (+sig) at α = 0.05.

Factor	μs				μk
	SS	Var	F-Value	Sig	SS	Var	F-Value	Sig
A	19.18	9.59	0.53	−0.23	3.44	1.72	0.36	−0.26
B	32.62	16.31	0.89	−0.16	6.46	3.23	0.67	−0.19
C	21.30	10.65	0.58	−0.22	1.91	0.96	0.20	−0.32
D	111.64	55.82	3.06	0.11	29.48	14.74	3.05	0.14
SST	330.79				80.02
Error	146.06	18.26			38.72	4.84

, a positive correlation for factor effect is evident from the positive significance value of Factor D across μ_s and μ_k in both DOE designs and for Factor B μ_k in L₉ (2¹ × 3³) results.

Although non-significant F-values recorded, a clear effect trend is visible; effect magnitude was highest for Factor D, followed by Factors B, A, and C.

Table 2 and Figure 5 and Figure 6 show that the effect of the tacky spray on the tested designs is measurable and coherent to the expected outcome, which provides a level of confidence in the use of the proposed method to investigate the effect of other relevant variables in future studies.

The speed had a minimal effect on friction performance; μ_s presented the same performance for mid and high speeds; however, μ_k performance was lower at the higher speed level.

5. Conclusions

The method proposed in this paper is appropriate to effectively evaluate the performance of various design parameters and their valid effects on friction performance. Follow up experimentation may follow testing parameters of speed and load more closely to the intended application of wheelchair racing. The design and applicability of bio-mimicry surfaces and textures for wheelchair racing glove design may still require more development and experimentation to achieve coupling optimization. There are currently other natural textures which may be readily available commercially, which may be of relevance to include in this type of experimental design in the short term.