Abstract
A high prevalence of shoulder injuries exists across the wheelchair using populations. To maintain competitive longevity and optimise performance, athletes must employ techniques which pose minimal injury risk. A computational model was used to assess relationships between the magnitude of reaction moments at the shoulder with key propulsion characteristics, including; contact and release angles, hand speed at contact, and joint angles at contact. Subject-specific musculoskeletal models (mass, maximum isometric force) for two elite wheelchair racing athletes were derived, and driven through kinetic and kinematic data obtained using motion capture. Greater reaction moments (min 72.6 Nm, max: 1077.8 Nm) at the shoulder were correlated with hand velocity (7.2 m/s–9.3 m/s) at contact (|r| > 0.866, p < 0.013), push time (|r| > 0.866, p < 0.013), and kinematic positioning at contact (|r| > 0.784, p < 0.020). Variations between athlete reaction force at the pushrim and joint reaction moments demonstrate the importance of coupled kinematic and modelling analysis in prescribing technique adaptations.
1. Introduction
Upper limb injuries are common amongst wheelchair athletes, particularly in the shoulder [1]. Research has identified that wheelchair racing, and road racing are amongst the greatest risk for sustaining a soft tissue injury [2]. As injuries to the upper extremity can both impede performance and limit the mobility of wheelchair using individuals and athletes, it is imperative that measures are taken to promote propulsion techniques which have low risk of promoting injury.
Athletes in wheelchair sports have demonstrated higher rates of shoulder, elbow-arm, and forearm-wrist injuries as compared to other Paralympic athletes [2]. The high incidence of injury can be attributed to the nature of the shoulder girdle being ill-equipped for the kinematic requirements of wheelchair propulsion. For example, the shoulder girdle, which is responsible for the majority of kinetic requirements of wheelchair propulsion, is structured to maximise freedom of movement [1]. However, in order to obtain maximum speed, athletes must apply large forces over short durations to achieve a high net impulse. The repeated, high loading of wheelchair propulsion contributes to injury in the shoulder-girdle construct [3].
Kinematic stroke patterns have been associated with injury risk, such as those with greater range of motion during the propulsion phases [1], when hands are in contact with the push rim, and when the peak reaction forces and moments occur [4]. Additionally, overuse has commonly been reported to increase injury risk [3], along with low movement variability [1].
Soft tissue injuries have been demonstrated as a leading injury amongst athletes in wheelchair sports specifically wheelchair racers [2]. Monitoring muscle loading requires an inherent understanding of both the forces and activation pattern of each muscle, to determine how much it is contributing to motion. As individual muscle forces, and joint reaction moments cannot be measured directly, computer simulations using musculoskeletal models are required.
The specific aim of this research was to evaluate whether a coupled kinematic investigation and computational simulation approach could effectively discern whether kinematic aspects of technique may lead to a greater injury risk. As shoulder injuries have typically been diagnosed as a consequence of the repeated, high impact loadings, in this research, it was hypothesised that a greater injury risk was associated with greater reaction joint moments.
2. Materials and Methods
2.1. Athlete Selection and Experimental Propulsion Task
Two female wheelchair racing athletes from the national level senior program were recruited for this study (A1: age = 24.4 years, mass = 52.9 kg, experience = 3 years, classification = T54; A2: age = 33.7 years, mass = 48.0 kg, experience = 23 years, classification = T53). Research was constrained to classifications demonstrating fair to good functional strength in the arms and partial (T53) to moderate (T54) trunk function [5]. Athletes provided written, informed consent, with ethical approval obtained by the University of Adelaide and the Australian Institute of Sport.
Athletes completed three steady state trials on a treadmill (H/P/Cosmos® Saturn, Traunstein, Germany) inclined to 1% [6]. Each trial was completed at a different speed, with the fastest belt speed comparable to individual regular race training velocity. A1 performed a treadmill familiarisation protocol prior to data collection, with A2 already demonstrating experience in treadmill propulsion. A five-minute active recovery period was provided between trials to minimise the effects of fatigue.
The front fork of the wheelchair was fastened to the treadmill using a custom designed clamp, which prevented lateral translations of the wheelchair, but allowed normal fore-aft movement of the wheelchair within a safe operating range. Both athletes complete treadmill based propulsion as part of regular training, suggesting any potential detriments to athlete performance from treadmill based propulsion within the recorded trials are minimal.
2.2. Measurement System
Kinematic data were obtained using both video (qualitative) and motion capture (quantitative). Motion capture data were collected using a 17 camera VICON Motion Analysis System (Oxford Metrics, Oxford, UK). Twenty three retro-reflective markers were located on the trunk and upper extremity (right side) using a cluster based marker set, and was calibrated as being accurate within 0.02 mm. Six of the markers were used for static joint center definition (at the shoulder, elbow and wrist), but were removed prior to the athlete completing the three trials. The remaining seventeen markers on the torso and upper extremity were used for kinematic tracking. Two cuff clusters (three markers each) were fixed on the acromion, and at the distal end of the humerus, in line with the medial epicondyle. An additional two T-bar clusters (three markers each) were located on the distal forearm, and at the hand, between the lateral epicondyle, ulnar styloid, and at the base of the second digit, which was affixed to the athlete’s glove. An additional five markers were located on the trunk segment, at the 7th cervical spinal process, 10th thoracic spinal process, at the sternum, and on the left and right posterior superior iliac spine. Eight markers were also located on the wheelchair, three being on the frame, and five on the wheel (one at the axle, two orthogonally on the pushrim; two orthogonally on the outer rim). These markers were used to establish athlete kinematics in relation to the wheelchair. Motion capture data were utilised to determine hand speed at contact, hand speed at release, and push time.
Three high speed Sony PXW-FS7 video cameras (located at the rear and perpendicularly left and right of the athlete-treadmill system) were utilised to validate the push durations. Cameras operated at a sampling frequency of 100 Hz and shutter speed of 1/1000 s. Video data were manually digitised (Kinovea v 0.8.15 www.kinovea.org) to identify contact and release angles, identified as the first and last frame where any part of the athlete’s hand or glove was in contact with the pushrim, respectively. Contact and release angles reported are measured with 0° located at top dead center of the wheel, with magnitude increasing in a clockwise direction. Angles were based on the ulna marker located on the hand from the VICON measurement.
2.3. Model Development
Computer simulations utilising the Wu Shoulder Musculoskeletal Model [7] were performed in OpenSim [8]. The musculoskeletal model was adapted to incorporate athlete-specific segment mass, and maximum isometric force generating capacity data. Segment masses were obtained through the assessment of DXA scans, as detailed by Laschowski et al. [9], whilst optimum isometric force generating capacity was established through an optimisation problem, iterating through strength factors. The optimum strength of the model was established through a convergence of muscle activation. The key range of motion analysed for this investigation is demonstrated in Figure 1. For trunk flexion angle, a value of −90° has the trunk parallel to the ground, with a value of 0° representing the athlete is in a conventional upright seating posture.
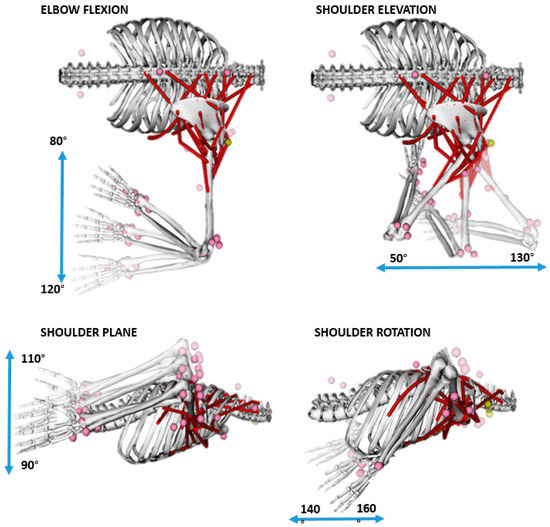
Figure 1.
Joint range of motions explored in this investigation.
Inverse kinematics calculations were used to reveal the trunk, shoulder joint and elbow flexion at contact, with specific timestamps established directly from motion capture data. Reaction forces were estimated from the kinematic data [10], whereby forces were estimated as a sum of the segment masses multiplied by their respective translational acceleration, and were used to drive the inverse dynamics calculations to obtain net joint reaction moments.
2.4. Statistical Analysis
Multiple regression analyses were performed to identify interactions between reaction moments and kinematic parameters. All statistical calculations were performed using IBM SPSS Statistics 21 Software for Windows (SPSS Inc., Chicago, IL, USA).
3. Results
Clear intra- and inter-athlete kinematic variation was observed, and is presented qualitatively in Figure 2, and quantitatively in Table 1. Key kinematic variations included release angle (A1: 218.9 ± 7.3°; A2: 180.9 ± 7.9°), shoulder elevation (A1: 52.1 ± 2.6°; A2: 91.7 ± 8.0°), shoulder plane (A1: −141.4 ± 5.9°; A2: −107.8 ± 2.0°), and elbow flexion (A1: 83.3 ± 3.1°; A2: 122.2 ± 4.8°). Figure 1 clearly demonstrates the different kinematic strategies employed by athletes with regards to head position and movement throughout motion. As the head segment was not modelled, it’s movement variability is not discussed.
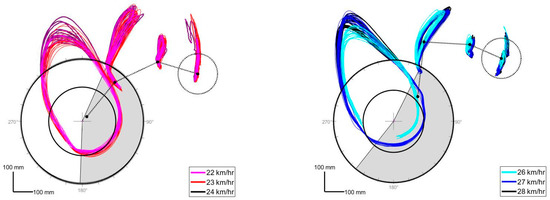
Figure 2.
Kinematic comparison of motion for A1 (left) and A2 (right). Time in contact with the wheel is represented by the grey regions, with guideline references located on the outside of the wheel. Segments presented represent the kinematic tracking of the head, shoulder, elbow and hand markers.

Table 1.
Kinematic and kinetic characteristics of propulsion presented as mean ±SD; n represents the number of push cycles recorded. * Represents data collected for a single side only. Contact and Release angles are presented to no decimal places to reflect precision of collected data.
Statistical analysis revealed that the reported shoulder joint reaction moments correlated with the athlete (Elevation: r = −0.947, p = 0.002; Rotation: r = 0.992, p = 0.000; Plane: r = 0.988, p = 0.000), speed (Elevation: r = −0.734, p = 0.048; Rotation: r = 0.899, p = 0.007; Plane: r = 0.903, p = 0.007), hand velocity at contact (Elevation: r = 0.875, p = 0.011; Rotation: r = −0.866, p = 0.013; Plane: r = −0.880, p = 0.010), and release (Elevation: r = 0.977, p = 0.000; Rotation: r = −0.891, p = 0.009; Plane: r = −0.891, p = 0.009), push time (Elevation: r = −0.866, p = 0.013; Rotation: r = 0.940, p = 0.003; Plane: r = 0.965, p = 0.001), release angle (Elevation: r = −0.928, p = 0.000; Rotation: r = 0.959, p = 0.001; Plane: r = 0.970, p = 0.001), trunk flexion angle (Elevation: r = −0.784, p = 0.020; Rotation: r = −0.807, p = 0.026; Plane: r = −0.834, p = 0.020) and shoulder elevation angle (Elevation: r = 0.925, p = 0.004; Rotation: r = −0.963, p = 0.001; Plane: r = −0.946, p = 0.002). Additional correlations were observed with elbow flexion angle (Rotation: r = −0.981, p = 0.000; Plane: r = −0.970, p = 0.001) and reaction force (Rotation: r = −0.817, p = 0.024; Plane: r = −0.801, p = 0.028).
4. Discussion
The aim of this research was to ascertain whether kinematic characteristics of motion could increase injury risk, and was assessed though coupling kinematic and computational modelling approaches. Greater joint reaction moments at the shoulder was the inferred mechanism for injury risk. With greater joint reaction moments, greater stresses are applied to the muscles spanning these joints, potentially generating a greater risk of overuse strain injury. Hand velocity at contact and release, push time, and joint angles at contact were key contributors to greater joint reaction moments. The magnitude of the reaction force, and the speed of propulsion were significantly correlated with greater shoulder plane and rotation moments. Athletes did not present with shoulder injuries at the time of testing.
Clear variations in kinematic strategies were employed between the two athletes, with a clear point of distinction being the hand speed at contact. A1 demonstrated a greater hand speed at contact, as well as a shorter push time (approximately 2/3 that of A2). In performance terms, this is indicative of a compromised transfer of force between the athlete and wheelchair. This may explain the reduced average race velocity as compared with A2, who is a World Champion level athlete. Biomechanically, due to the shorter push time, and potentially greater hand speed at contact, A1 experiences a much greater impulse with each contact, which can be translated in the estimated reaction force data. It is interesting to observe however, that despite this, all reported shoulder joint reaction moments are smaller in A1. It can be inferred that A1 adopts a technique which minimises moment arms, effectively reducing the reaction loads passing through the arm and acting at the shoulder. It can hence be suggested that the largely different kinematic position at contact may be reducing the likelihood of the athlete in sustaining a soft tissue injury to the shoulder. It is important to highlight that athletes must optimise the balance between biomechanical stability for injury prevention, and required dynamism for competitive advantage. Through utilising this coupled kinematic and modelling analysis approach, athletes can modify techniques with the aim of improved performance, however also reaping the benefits of reduced risk of soft tissue injury.
The clear inter-individual variations observed can be likened to difference in classification, and the degree of trunk control (present in A1 only, as supported by trunk flexion angle). Additionally, A2 demonstrated >10 years of international experience. Inter-individual variations across speeds are consistent with the literature, and can be explained by the fastest speed being representative of race velocity, whilst the other two are sub-maximal efforts, where athletes may have greater control over technique. When considering the kinematic parameters alone, A2 demonstrated greater consistency across each of the speeds, which can potentially be attributed to experience. It is assumed that as both athletes were female, performed at comparable speeds, and had similar classification, the results presented in this research are more homogenous than would be characteristic of the entire population.
Due to the small sample size of this research correlations presented in this research cannot be formally generalised. This research has identified that elbow angle and shoulder elevation and plane angles are correlated with greater joint reaction moments. Hence, the continuation, and expansion of this work in developing a database of normative values may better promote kinematic techniques which are less likely to result in athlete injury. However, these techniques will also be reliant on the unique physical impairments and capabilities of each athlete. Furthermore, this research examined a simplistic approach to the diagnosis of athlete injury, focusing solely on increased joint moments being the causative factor, without consideration of interaction effects with other performance aspects. It is also plausible that additional factors, including highly consistent techniques (repeatedly straining the same tissues) may also contribute to injury, and should be explored further.
It is acknowledged that simulation of only the right-hand side of the body is a limitation of this research, as temporal asymmetries have been observed for both athletes. Both athletes exhibit complete spinal cord injuries, with less pronounced asymmetries as compared to athletes with incomplete spinal cord lesions. Additionally, both athletes are competitive in classifications having full physical function in their upper extremities. Therefore, it can be inferred that there is reasonable agreement between the left and right limbs, and it is unlikely that the reported kinematic parameters would vary largely.
5. Conclusions
This research has demonstrated the potential impact of using a coupled kinematic and modelling approach as a performance assessment tool to better ascertain relationships between kinematic technique and injury. Increased shoulder loading is a compounding effect of numerous kinematic parameters, with clear differences observed in the kinematic strategies utilised by the athletes in this research. Through coupling regular kinematic feedback with a biomechanical model, it is possible to balance the performance and injury-risk requirements of propulsion.
Acknowledgments
The authors would like to thank Keren Faulkner (Australian Paralympic Committee, Adelaide, Australia), Joseph Winter (Australian Institute of Sport, Leverrier St, Australia) for their contributions to this research. The authors would also like to thank the Australian Government Training Research Program Scholarship for assisting the research.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Churton, E.; Keogh, J. Constraints influencing sports wheelchair propulsion performance and injury risk. BMC Sports Sci. Med. Rehabil. 2013, 5, 1–10. [Google Scholar] [CrossRef]
- Curtis, K.A.; Dillon, D.A. Survey of wheelchair athletic injuries: Common patterns and prevention. Paraplegia 1985, 23, 170–175. [Google Scholar] [CrossRef]
- Curtis, K.A.; Black, K. Shoulder pain in female wheelchair basketball players. J. Orthop. Sports Phys. Ther. 1999, 29, 225–231. [Google Scholar] [CrossRef]
- Rankin, J.W.; Kwarciak, A.M.; Richter, W.M.; Neptune, R.R. The influence of wheelchair propulsion technique on upper extremity muscle demand: A simulation study. Clin. Biomech. 2012, 27, 879–886. [Google Scholar] [CrossRef] [PubMed]
- Tweedy, S. IPC Athletics Classification Project for Physical Impairments; Final Report—Stage 1; International Paralympic Committee Athletics: Bonn, Germany, 2010; p. 107. [Google Scholar]
- Mason, B.; Lenton, J.; Leicht, C.; Goosey-Tolfrey, V. A physiological and biomechanical comparison of over-ground, treadmill and ergometer wheelchair propulsion. J. Sports Sci. 2014, 32, 78–91. [Google Scholar] [CrossRef] [PubMed]
- Wu, W.; Lee, P.V.S.; Bryant, A.L.; Galea, M.; Ackland, D.C. Subject-specific musculoskeletal modeling in the evaluation of shoulder muscle and joint function. J. Biomech. 2016, 49, 3626–3634. [Google Scholar] [CrossRef] [PubMed]
- Delp, S.L.; Anderson, F.C.; Arnold, A.S.; Loan, P.; Habib, A.; John, C.T.; Guendelman, E.; Thelen, D.G. OpenSim: Open-source software to create and analyze dynamic simulations of movement. IEEE Trans. Biomed. Eng. 2007, 54, 1940–1950. [Google Scholar] [CrossRef]
- Laschowski, B.; McPhee, J. Body segment parameters of Paralympic athletes from dual-energy X-ray absorptiometry. Sports Eng. 2016, 19, 155–162. [Google Scholar] [CrossRef]
- Ren, L.; Jones, R.K.; Howard, D. Whole body inverse dynamics over a complete gait cycle based only on measured kinematics. J. Biomech. 2008, 41, 2750–2759. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).