The Golf Shaft’s Influence on Clubhead-Ball Impact Dynamics †
Abstract
:1. Introduction
2. Experimental
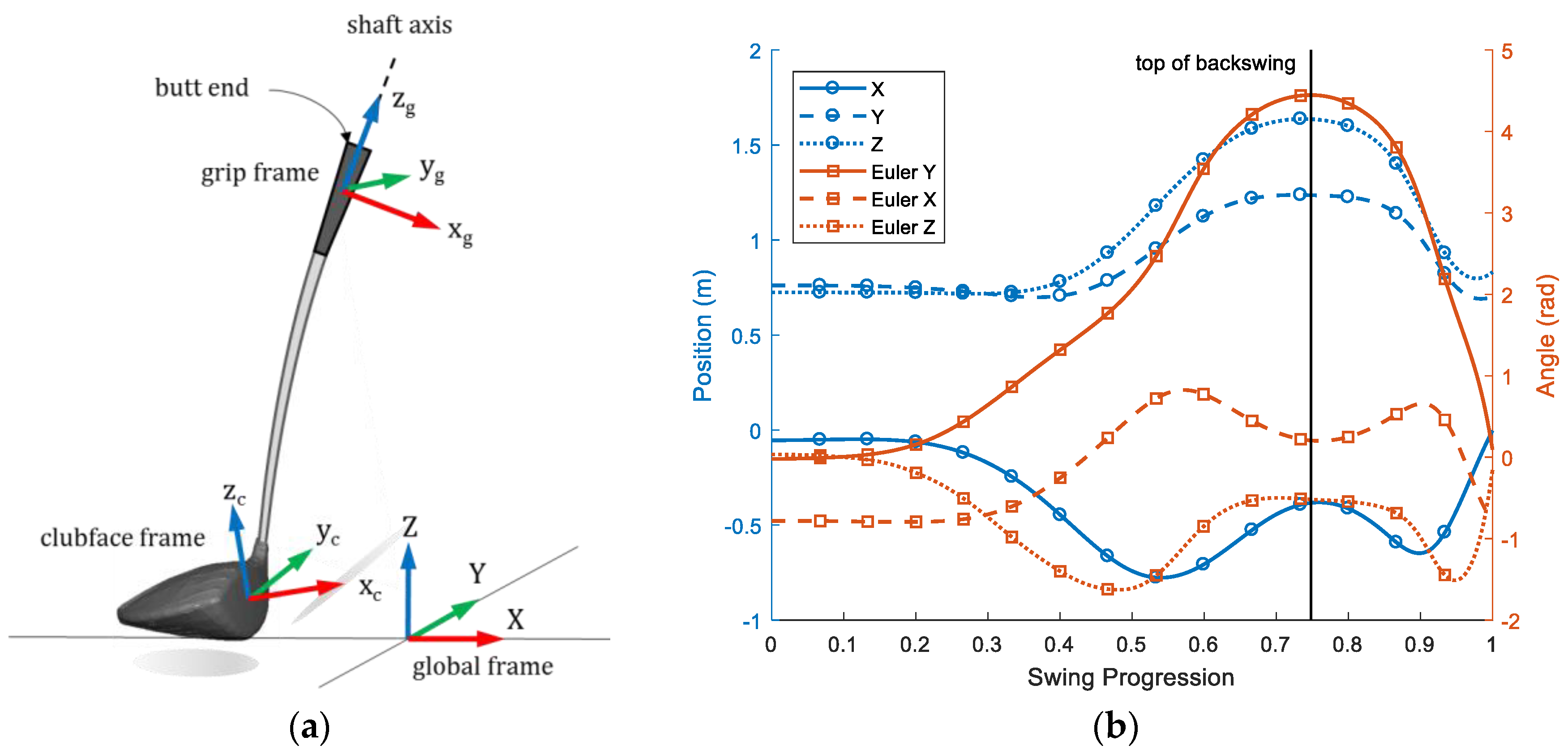
2.1. Motion Capture
2.2. Club Properties
3. Modelling
3.1. Flexible Club & Swing Simulation
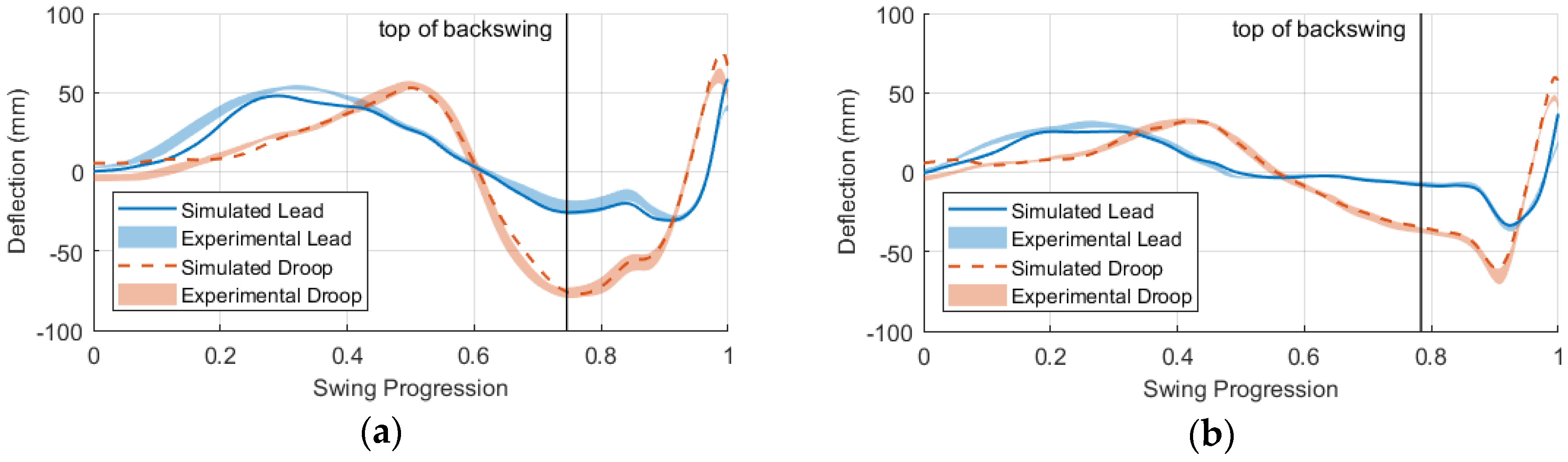
3.2. Flexible Club Validation
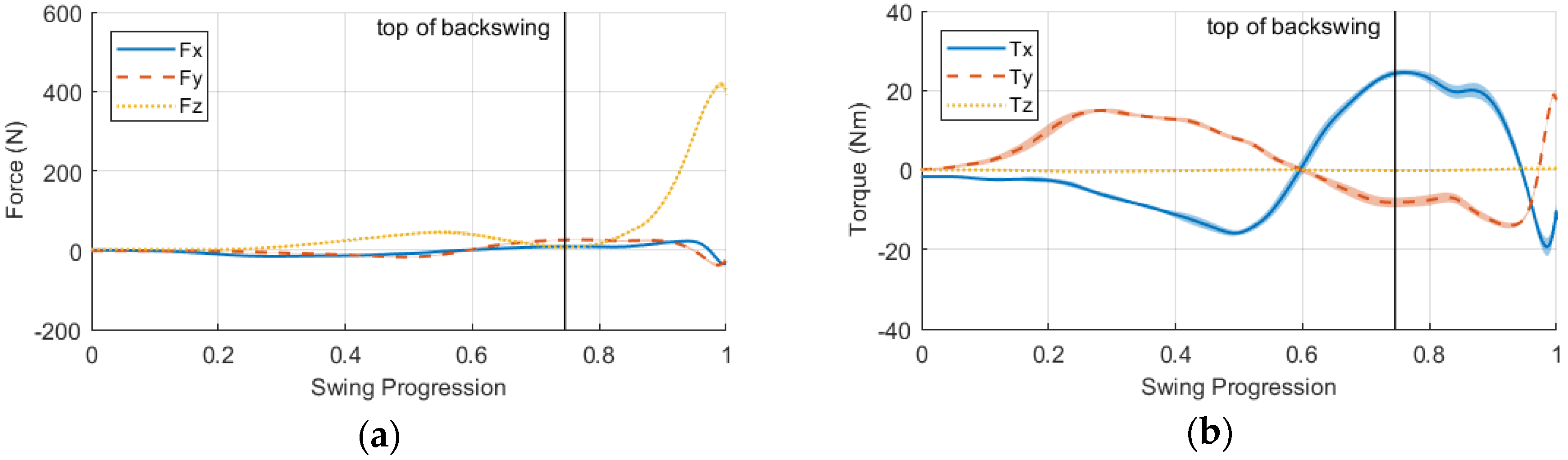
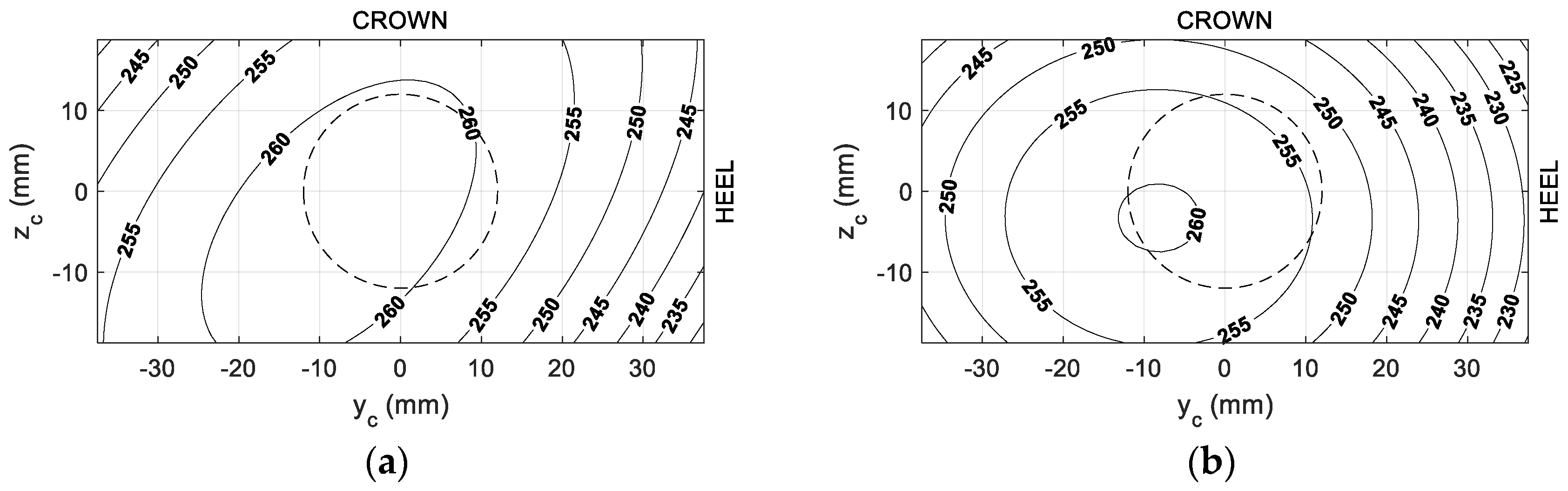
3.3. Impact Model and Validation
4. Simulation Results, Discussion & Conclusions
Acknowledgments
Conflicts of Interest
References
- Cochran, A.J.; Stobbs, J. Search for the Perfect Swing; Triumph: Hinckley, UK, 2005. [Google Scholar]
- Tanaka, K.; Oodaira, H.; Teranishi, Y.; Sato, F.; Ujihashi, S. Finite-element analysis of the collision and bounce between a golf ball and simplified clubs. In The Engineering of Sport 7; Springer: Paris, France, 2009; pp. 653–662. [Google Scholar]
- Cross, R.; Nathan, A.M. Experimental study of the gear effect in ball collisions. Am. J. Phys. 2007, 75, 658–664. [Google Scholar] [CrossRef]
- United States Golf Association and R&A Rules Limited (USGA). Procedure for Measuring the Moment of Inertia of Golf Clubheads; USGA: Far Hills, NJ, USA, 2006. [Google Scholar]
- Schmitke, C.; McPhee, J. Using linear graph theory and the principle of orthogonality to model multibody, multi-domain systems. Adv. Eng. Inform. 2008, 22, 147–160. [Google Scholar] [CrossRef]
- Sandhu, S.; Millard, M.; McPhee, J.; Brekke, D. 3D dynamic modelling and simulation of a golf drive. Procedia Eng. 2010, 2, 3243–3248. [Google Scholar] [CrossRef]
- Gonthier, Y.; McPhee, J.; Lange, C.; Piedboeuf, J.C. A contact modeling method based on volumetric properties. In Proceedings of the ASME 5th International Conference on Multibody Systems, Nonlinear Dynamics and Control, Long Beach, CA, USA, 24–28 September 2005; Volume 5, pp. 477–486. [Google Scholar]
- Brown, P.; McPhee, J. A continuous velocity-based friction model for dynamics and control with physically meaningful parameters. J. Comput. Nonlinear Dyn. 2016, 11. [Google Scholar] [CrossRef]
- Nesbit, S. A three dimensional kinematic and kinetic study of the golf swing. J. Sports Sci. Med. 2005, 4, 499–519. [Google Scholar] [PubMed]

| Dataset | Ball Speed (km/h) | Launch Angle (deg) | Azimuth (deg) | Back Spin (rpm) | Side Spin (rpm) |
|---|---|---|---|---|---|
| Training | −0.24 ± 1.60 | 1.00 ± 0.33 | 0.16 ± 0.69 | −59.4 ± 334 | 184 ± 286 |
| Test | 0.17 ± 1.96 | 0.93 ± 0.39 | −0.15 ± 0.54 | −150 ± 287 | 239 ± 269 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
McNally, W.; McPhee, J.; Henrikson, E. The Golf Shaft’s Influence on Clubhead-Ball Impact Dynamics. Proceedings 2018, 2, 245. https://doi.org/10.3390/proceedings2060245
McNally W, McPhee J, Henrikson E. The Golf Shaft’s Influence on Clubhead-Ball Impact Dynamics. Proceedings. 2018; 2(6):245. https://doi.org/10.3390/proceedings2060245
Chicago/Turabian StyleMcNally, William, John McPhee, and Erik Henrikson. 2018. "The Golf Shaft’s Influence on Clubhead-Ball Impact Dynamics" Proceedings 2, no. 6: 245. https://doi.org/10.3390/proceedings2060245
APA StyleMcNally, W., McPhee, J., & Henrikson, E. (2018). The Golf Shaft’s Influence on Clubhead-Ball Impact Dynamics. Proceedings, 2(6), 245. https://doi.org/10.3390/proceedings2060245






