Analysis of Sway in Ballroom Dancing ^†

Abstract

According to syllabi of ballroom dancing, the sway is explained as the inclination of the body towards the inside of the turn. This explanation is questionable and a more adequate explanation is given based on a mechanical analysis with a new concept of inclination and bending sways. First, the sway mechanism is explained as the balance of the inertia force and the inclination using one-element model. Further a two-element model is introduced including both the inclination and the bending effects. The model explains the control and stability of sway. The sway process is classified into three stages, and the change of the inclination and bending with time is demonstrated by the analysis. The understanding of sway mechanism improves the dancers′ swing movements.

1. Introduction

Ballroom dancing techniques have been developed and systematized in 20th century [1,2,3,4,5,6]. Sway is one of the important technical terms especially in Modern Standard dances. It is defined as the inclination of the body away from the moving foot and towards the inside of the turn [4] and indicated in each step of the figures in the syllabus [4]. The inclination of the body is seen in other sports such as running, skating, skiing, motorcycle, etc., although the term “Sway” is not always used. In many cases, this inclination is induced in the movement of turning, so that it has been explained using centrifugal force.

Sway in ballroom dancing is also often explained as the balancing with the centrifugal force in turning. However, in most of the turns in ballroom dancing, the translational movement of the body is almost straight except some curving figures. The main component of turn is regarded as the rotation around the body axis (center of gravity), so that the expression “centrifugal force” is not adequate. Actually, the translational body movement with acceleration and deceleration is more important than the rotation as the “inertia force” to be balanced.

From a mechanical point of view, the inclination of the body can be analyzed in any direction, however, since Sway in ballroom dancing is in side direction of the body (in the coronal plane), the forward or backward inclination (in the sagittal plane) is excluded in the analysis. Sway usually appears in the swing dances (Waltz, Foxtrot, Quickstep and Viennese Waltz), however, the present analysis may be applied to other dances and sports.

2. Fundamental Analysis by the Use of One-Element Model

2.1. Ansalysis

Since Sway is considered to balance to the inertia force, the amount of inertia is estimated first. The movement in the Waltz Natural Turn is examined as an example. As the swing movement in the horizontal direction x, a sinusoidal function is adapted in the analysis.

$$x_{\mathrm{G}}=\frac{L}{T}\left\{t-\frac{T}{2\pi }\sin 2\pi \left(\frac{t}{T}\right)\right\},\frac{\mathrm{d}{x}_{\mathrm{G}}}{\mathrm{d}t}=\frac{L}{T}\left\{1-\cos 2\pi \left(\frac{t}{T}\right)\right\},\frac{{\mathrm{d}}^2{x}_{\mathrm{G}}}{\mathrm{d}{t}^2}=\frac{2\pi L}{T^2}\sin 2\pi \left(\frac{t}{T}\right)$$

(1)

where T and L are the period and wave length of the swing wave, respectively, and $x_{\mathrm{G}}$ is the position of center of gravity. In the natural turn, Sway occurs on Count 2 and 3, in the deceleration stage and the largest deceleration is $\frac{{\mathrm{d}}^2{x}_{\mathrm{G}}}{\mathrm{d}{t}^2}=-\frac{2\pi L}{T^2}$. The value is −3.14 m/s² when is L = 2 m and music tempo is 30 bpm.

Next, the force induced by the inclination is examined by using a one-element model. The dancer′s body is represented by a bar, inclined slightly from the vertical axis with the lower end touched to the floor at the origin. The positions of center of gravity and its mass are denoted as $(x_{\mathrm{G}},y_{\mathrm{G}})$, and m, respectively. The inclination angle θ is assumed to be small so that the height of the center of gravity $y_{\mathrm{G}}$ is regarded as constant and $x_{\mathrm{G}}\cong y_{\mathrm{G}}\theta$. The equation of motion becomes,

$$y_{\mathrm{G}}\frac{{\mathrm{d}}^2\theta }{\mathrm{d}{t}^2}=g\theta$$

(2)

The solution of the differential equation has a hyperbolic function form, but for small range of θ, it can be approximated by a linear function. Comparing (2) with the sinusoidal relation (1) leads the following relation.

$$\theta =\left(\frac{{\mathrm{d}}^2{x}_{\mathrm{G}}}{\mathrm{d}{t}^2}\right)/g,\mathrm{and}\mathrm{the}\mathrm{largest}\mathrm{deceleration}\mathrm{is}{\theta }_{\max }={\left|\frac{{\mathrm{d}}^2{x}_{\mathrm{G}}}{\mathrm{d}{t}^2}\right|}_{\max }/g=\frac{2\pi L}{T^{2}g}.$$

(3)

As an example, in the case mentioned above, L = 2 and 30 bpm, the largest inclination is θ = 0.32 rad, and in case of L = 1.5 m and 28 bpm, $\theta =0.21$. These values seem reasonable so that the relation between the inclination and the inertia force is intuitively acceptable though the analysis in this section is not exact.

2.2. Deceleration and Acceleration Due to Sway

The Sway in ballroom dancing usually occurs in the deceleration stage, as stated above, i.e., the inclination of the body opposes the moving direction of the body. However, in some figures, the inclination is in the same direction as the progression of the body in which case, the body movement becomes accelerated. Hover Feather is one such case. Another interesting case is found in Turning lock to Right. Normal Turning lock has Sway against the progression of body so that deceleration occurs, however, in case of Turning lock to Right, either Sway to R or Sway to L is acceptable. When the Sway is in the progression direction, it is understood that the body movement is accelerating.

3. Advanced Analysis by the Use of Two-Element Model

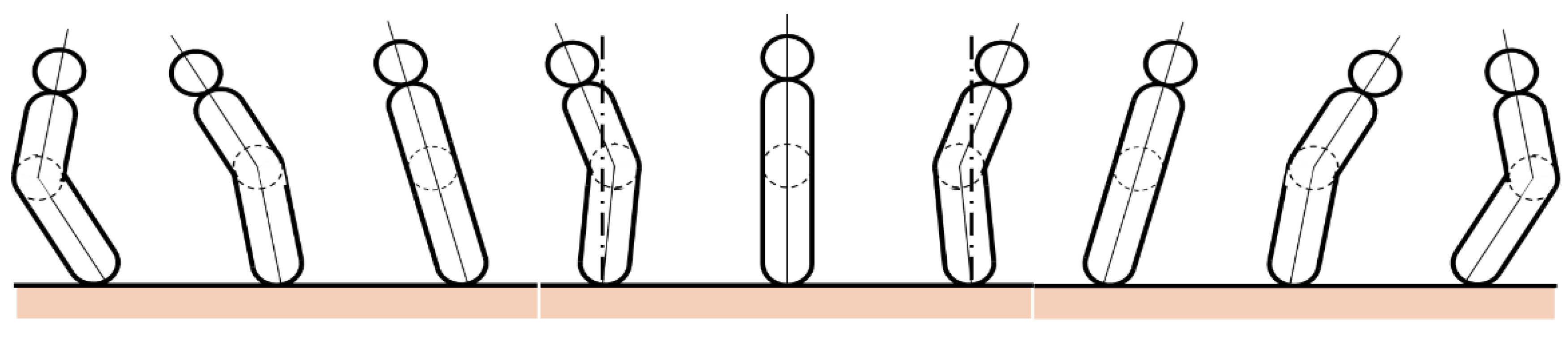
3.1. New Deffinition of Sway Describing Inclination and Bending

Sway in the syllabus is defined as the inclination of the body, however, actual inclination of the dancer′s center of gravity to the vertical axis does not always meet this definition. In fact, on the third step of the natural turn, Sway continues to remain in spite of no acceleration. In order to solve this contradiction, a new concept of Sway is proposed. Inclination Sway and Bending Sway are newly defined. Inclination Sway is defined as the inclination of center of gravity to the vertical axis which is the same as mentioned in the one-element model. Bending Sway is the bending of the body in the side direction, which is felt by the dancer through the muscle, and also visible by the observers so that generally recognized as Sway described in each figure in the syllabus.

The Sway is described is such as right (R), left (L), or straight (S). These combinations of Sway are illustrated in Figure 1.

These combinations of Sway are often seen in other sports, such as motorcycle riding, skiing, skating, etc. In the case of the motorcycle, the terms “Lean in”, “Lean out” and “Lean with” are used.

3.2. Two-Element Model Analysis

The two-element sway model proposed here is illustrated in Figure 2. The dancer′s body is represented by a vertical bar which is bent at a hinge. The hinge position is denoted by $x=x_{\mathrm{H}}$, $y=y_{\mathrm{H}}$. The positions of center of gravity and the mass of upper and the lower part are denoted as $(x_{\mathrm{U}},y_{\mathrm{U}})$, $m_{\mathrm{U}}$ and $(x_{\mathrm{L}},y_{\mathrm{L}})$, $m_{\mathrm{L}}$, respectively. The total mass is $m=m_{\mathrm{U}}+m_{\mathrm{L}}$. The sway angle is assumed to be small so that all the $y$ components are regarded as constant. The normalized mass is $m_{\mathrm{U}}\prime =m_{\mathrm{U}}/m$,$m_{\mathrm{L}}\prime =m_{\mathrm{L}}/m$.

The inclination of total body $\theta$ and the bending angle at the hinge $\phi$ are expressed as,

$$\theta =\frac{m_{\mathrm{U}}{x}_{\mathrm{U}}}{m_{\mathrm{U}}{y}_{\mathrm{U}}+m_L{y}_{\mathrm{L}}}+\frac{m_L{x}_{\mathrm{L}}}{m_{\mathrm{U}}{y}_{\mathrm{U}}+m_L{y}_{\mathrm{L}}}\phi =\frac{x_U}{\left(y_U-y_{\mathrm{H}}\right)}-\frac{y_U}{y_{\mathrm{L}}\left(y_U-y_{\mathrm{H}}\right)}{x}_{\mathrm{L}},$$

(4)

Respectively. The hinge moment $M_{\mathrm{H}}$ is considered to be a variable controlled by the dancer. The equilibrium equations for the upper element and the lower element together with the connecting hinge condition converges to the following differential equation.

$$\frac{{\mathrm{d}}^2\theta }{\mathrm{d}{t}^2}=\frac{m_{\mathrm{U}}{y}_{\mathrm{U}}+m_{\mathrm{L}}{y}_{\mathrm{L}}}{m_{\mathrm{U}}{y}_{\mathrm{U}}{}^2+m_{\mathrm{L}}{y}_{\mathrm{L}}{}^2}g\theta +\frac{m_{\mathrm{U}}{m}_{\mathrm{L}}{y}_{\mathrm{L}}\left(y_U-y_{\mathrm{H}}\right)\left(y_U-y_{\mathrm{L}}\right)}{\left(m_{\mathrm{U}}{y}_{\mathrm{U}}+m_{\mathrm{L}}{y}_{\mathrm{L}}\right)\left(m_{\mathrm{U}}{y}_{\mathrm{U}}{}^2+m_{\mathrm{L}}{y}_{\mathrm{L}}{}^2\right)}\frac{{\mathrm{d}}^2\phi }{\mathrm{d}{t}^2}$$

(5)

The first term in the right-side part of the equation expresses the solution for the fixed hinge angle case, i.e., the solution for the one-element model. The second term represents the effect of the acceleration of hinge angle change. Since the stable solution cannot be obtained at θ = 0 without this second term, Bending Sway is necessary to control the stability. The above equation is rewritten in a simple form by introducing normalized parameters, as,

$$\frac{{\mathrm{d}}^2\phi \prime }{\mathrm{d}t{\prime }^2}=-\left(\frac{{\mathrm{d}}^2\theta \prime }{\mathrm{d}t{\prime }^2}\right)+Q\prime \theta \prime ,$$

(6)

where the normalized parameters are,

$$\begin{gathered} \phi \prime =\phi /P,{\theta }^{\prime }=\left(y_{\mathrm{G}}/L\right)\theta ,t^{\prime }=t/T, \\ {Q}^{\prime }=\left\{1-\frac{{m_{\mathrm{U}}}^{\prime }{m_{\mathrm{L}}}^{\prime }{\left(y_U-y_{\mathrm{L}}\right)}^2}{\left({m_{\mathrm{U}}}^{\prime }{y}_{\mathrm{U}}{}^2+{m_{\mathrm{L}}}^{\prime }{y}_{\mathrm{L}}{}^2\right)}\right\}\left(\frac{g{T}^2}{y_{\mathrm{G}}}\right),P=\frac{\left({m_{\mathrm{U}}}^{\prime }{y}_{\mathrm{U}}{}^2+{m_{\mathrm{L}}}^{\prime }{y}_{\mathrm{L}}{}^2\right)}{{m_{\mathrm{U}}}^{\prime }{m_{\mathrm{L}}}^{\prime }{y}_{\mathrm{L}}\left(y_U-y_{\mathrm{H}}\right)}\frac{y_{\mathrm{G}}}{\left(y_U-y_{\mathrm{L}}\right)}. \end{gathered}$$

(7)

The advantage of normalization is to express the effect of dancer′s physical dimensions and the music speed with fewer parameters.

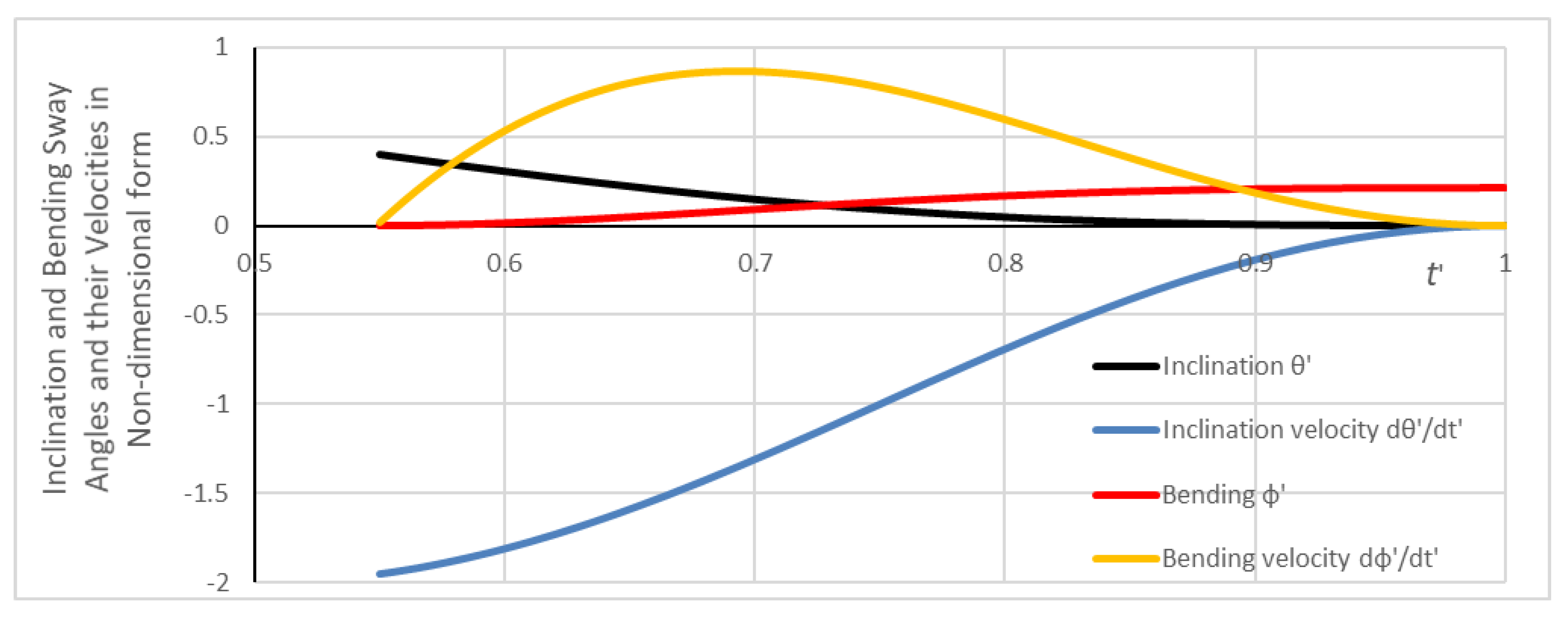
3.3. Process of Sway Development

Since the deceleration diminishes at the end of swing, Inclination Sway decreases towards the end of swing and instead the bending sway increases and remains. Under this consideration, the progression of sway is explained here classifying into 3 stages; Developing stage, Maintaining stage and Diminishing stage. The analysis shows the progression of Inclination Sway $\theta \prime \left(t\prime \right)$ and Bending Sway $\phi \prime \left(t\prime \right)$ with time in normalized form.

3.3.1. Sway Developing Stage

Sway is generated most often in the latter part of swing. It is explained taking example of 1–3 of Man′s natural turn. On step 1, the body faces almost to the moving direction so that Sway can be neglected. As the facing direction deviates from the moving direction due to CBM, Sway must be considered. Sway becomes important when the body movement turns from acceleration to deceleration. During the body weight is supported by two feet (step 1 and 2), the balance is kept by the two feet. As the body weight is transferred mostly on step 2 (left foot), the role of Sway becomes predominant. In case of the Waltz, since the rise is continued to the middle of Count 3 (the third beat in a bar), the end of swing is also at the middle of Count 3 (Step 3), whereas, in Foxtrot or Quickstep, there is no rise on Step 3 so that the swing finishes at the end of Step 2. In any case, the formation of Inclination Sway commences with the start of the swing and diminishes at the end of swing. Bending sway is produced to match the balance of the center of gravity.

As the swing movement in the horizontal direction (Inclination Sway θ′), a sinusoidal function is adapted in the analysis as in the one-element analysis.

$$\frac{{\mathrm{d}}^2\theta \prime }{\mathrm{d}t{\prime }^2}=-2\pi \sin \left(2\pi t\prime \right)\frac{\mathrm{d}\theta \prime }{\mathrm{d}t\prime }=-1+\cos \left(2\pi t\prime \right)\theta \prime =1-t\prime +\frac{1}{2\pi }\sin \left(2\pi t\prime \right).$$

(8)

The corresponding differential equation is

$${\left(\frac{1}{2\pi }\right)}^2\frac{{\mathrm{d}}^2\theta \prime }{\mathrm{d}t{\prime }^2}+\theta \prime =\left(1-t\prime \right).$$

(9)

The condition of Inclination Sway θ′ at the start, t′ = 0, and at the end, t′ = 1 of swing are

$$\theta \prime \left(0\right)=\theta {\prime }_0=1,\frac{\mathrm{d}\theta \prime }{\mathrm{d}t\prime }\left(0\right)=0,\mathrm{and}\theta \prime \left(1\right)=0,\frac{\mathrm{d}\theta \prime }{\mathrm{d}t\prime }\left(1\right)=0.$$

(10)

The condition of Bending Sway $\phi \prime$ at the start, $t\prime =t{\prime }_{\mathrm{S}}$, and at the end, t′ = 1 are

$$\phi \prime \left(t{\prime }_{\mathrm{S}}\right)=0,\frac{\mathrm{d}\phi \prime }{\mathrm{d}t\prime }\left(t{\prime }_{\mathrm{S}}\right)=0,\mathrm{and}\frac{\mathrm{d}\phi \prime }{\mathrm{d}t\prime }\left(1\right)=0,\frac{{\mathrm{d}}^2\phi \prime }{\mathrm{d}t{\prime }^2}\left(1\right)=0.$$

(11)

The equation of motion is solved with the above conditions as

$$\frac{{\mathrm{d}}^2\phi \prime }{\mathrm{d}t{\prime }^2}=\left\{\left(\frac{1}{2\pi }\right)Q\prime +2\pi \right\}\sin \left(2\pi t\prime \right)+Q\prime \left(1-t\prime \right)$$

(12)

$$\frac{\mathrm{d}\phi \prime }{\mathrm{d}t\prime }=\left\{{\left(\frac{1}{2\pi }\right)}^{2}Q\prime +1\right\}\left\{1-\cos \left(2\pi t\prime \right)\right\}-\frac{1}{2}Q\prime {\left(1-t\prime \right)}^2$$

(13)

$$\phi \prime =\left\{{\left(\frac{1}{2\pi }\right)}^{2}Q\prime +1\right\}\left(t\prime -t{\prime }_{\mathrm{S}}\right)-\left(\frac{1}{2\pi }\right)\left\{{\left(\frac{1}{2\pi }\right)}^{2}Q\prime +1\right\}\left\{\sin \left(2\pi t\prime \right)-\sin \left(2\pi t{\prime }_{\mathrm{S}}\right)\right\}+\frac{1}{6}Q\prime \left\{{\left(1-t\prime \right)}^3-{\left(1-t{\prime }_{\mathrm{S}}\right)}^3\right\}$$

(14)

The Bending start time $t\prime =t{\prime }_{\mathrm{S}}$ is given as the time which satisfies $\left(\mathrm{d}\phi \prime /\mathrm{d}t\prime \right)=0$. Example of the development of Inclination and Bending is shown in Figure 3.

3.3.2. Sway Maintaining Stage

Bending sway is kept constant without Inclination sway in this stage. The hinge moment $M_{\mathrm{H}}$ is kept constant.

$$\mathrm{Inclination}\mathrm{Sway}\theta \prime \left(t\prime \right)=0\frac{\mathrm{d}\theta \prime }{\mathrm{d}t\prime }=0\frac{{\mathrm{d}}^2\theta \prime }{\mathrm{d}t{\prime }^2}=0$$

(15)

$$\mathrm{Bending}\mathrm{Sway}\phi \prime \left(t\prime \right)=\phi {\prime }_0\left(\mathrm{Constant}\right)\frac{\mathrm{d}\phi \prime }{\mathrm{d}t\prime }=0\frac{{\mathrm{d}}^2\phi \prime }{\mathrm{d}t{\prime }^2}=0$$

(16)

3.3.3. Sway Diminishing Stage

This stage starts in the condition of existing sway and ends in the equilibrium state without sway. A typical condition is that there is already no inertia force from the start, i.e., no inclination sway at the start, so that the process can be regarded as the bending sway diminishing process. The initial condition at t′ = 0, and at the end condition at t′ = 1 are,

$$\theta \prime \left(0\right)=0,\frac{\mathrm{d}\theta \prime }{\mathrm{d}t\prime }\left(0\right)=0,\phi \prime \left(0\right)=\phi {\prime }_{\mathrm{S}},\frac{\mathrm{d}\phi \prime }{\mathrm{d}t\prime }\left(0\right)=0,\mathrm{and}\phi \prime \left(1\right)=0\frac{\mathrm{d}\phi \prime }{\mathrm{d}t\prime }\left(1\right)=0.$$

(17)

The diminishing manner is also assumed to be harmonic, here, i.e.,

$$\left(\frac{1}{\phi {\prime }_{\mathrm{S}}}\right)\phi \prime =\left\{1-t\prime +\frac{1}{2\pi }\sin \left(2\pi t\prime \right)\right\},\left(\frac{1}{\phi {\prime }_{\mathrm{S}}}\right)\frac{\mathrm{d}\phi \prime }{\mathrm{d}t\prime }=-\left\{1-\cos \left(2\pi t\prime \right)\right\},\left(\frac{1}{\phi {\prime }_{\mathrm{S}}}\right)\frac{{\mathrm{d}}^2\phi \prime }{\mathrm{d}t{\prime }^2}=-\left(2\pi \right)\sin \left(2\pi t\prime \right).$$

(18)

The corresponding solution for the inclination becomes,

$$\left(\frac{1}{\phi {\prime }_{\mathrm{S}}}\right)\theta \prime =\frac{2\pi }{Q\prime +{\left(2\pi \right)}^2}\left\{-\sin \left(2\pi t\prime \right)+\left(2\pi \right)Q{\prime }^{-\frac{1}{2}}\sinh \left(Q{\prime }^{\frac{1}{2}}t\prime \right)\right\}$$

(19)

The solution satisfies the condition at $t\prime =0$, with increasing with time. The real inclination θ is given as $\theta \prime =\left(y_{\mathrm{G}}/L\right)\theta$ so that it cannot become remarkably large, provided that the lateral movement of body L is small. In the actual process, the body weight is transferred to the other foot before the end of the process.

4. Discussion and Conclusions

The swing analysis [7] has shown that the size of dancer does not affect the vertical swing movement. However, the present sway analysis, the parameter is the ratio between the height of center of gravity of body and the swing distance (the stride of step).

Through understanding of sway mechanism dancers can improve their sway movement, knowing which case the sway is necessary or not. The knowledge of sway mechanism can also give useful advice in developing dancer′s aid or artificial dancer.

Conclusions of Present Analysis

It is more appropriate to explain Sway in terms of inertia force during the dance movement rather than in terms of the centrifugal force. The sway mechanism should be analyzed by clarifying the distinction of the inclination and the bending of the body. The one-element model analysis has shown the relation between the inclination of the body and the inertia force, and the amount of inclination by the analysis is quantitatively consistent with actual one supposing the natural harmonic movement of the body. The two-element model in the present analysis has explained the total process of sway progression, i.e., developing process, maintaining process, and diminishing process. Through the two-element model, the sway which balances the inertia force is shown to be different from the apparent sway been understood as the sway in the ballroom dancing syllabi. Bending sway is necessary in order to keep balancing on one foot. The present analysis can be applicable to other sports.