Analysis of Sway in Ballroom Dancing †
Abstract
:1. Introduction
2. Fundamental Analysis by the Use of One-Element Model
2.1. Ansalysis
2.2. Deceleration and Acceleration Due to Sway
3. Advanced Analysis by the Use of Two-Element Model
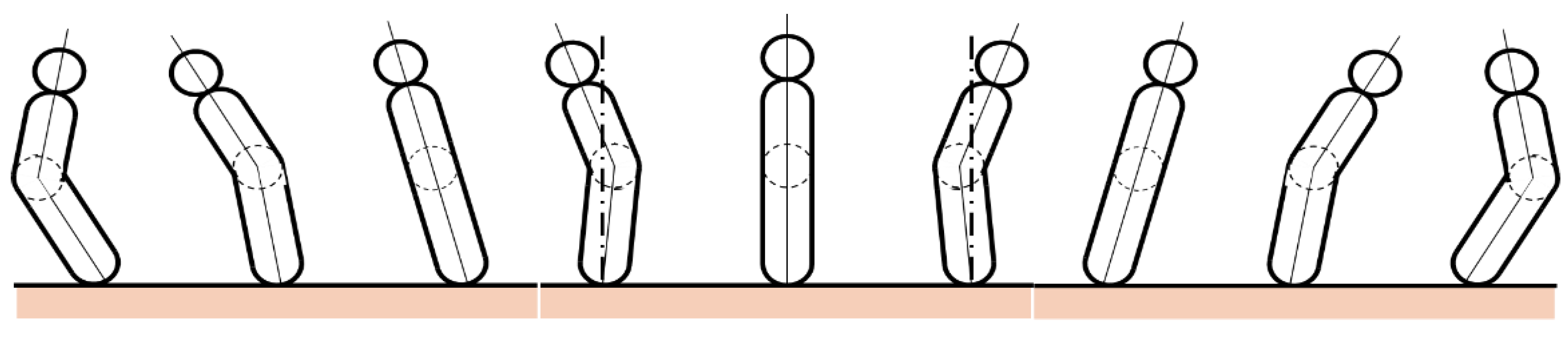
3.1. New Deffinition of Sway Describing Inclination and Bending
3.2. Two-Element Model Analysis
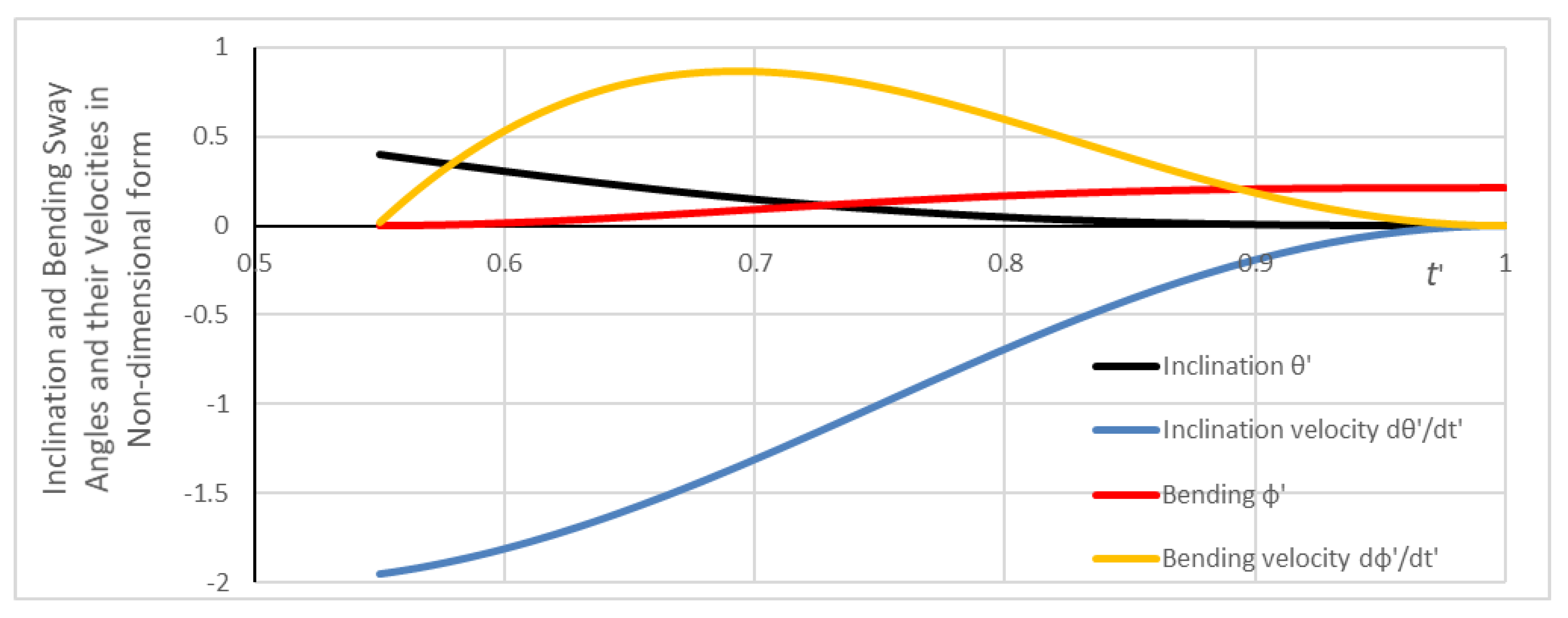
3.3. Process of Sway Development
3.3.1. Sway Developing Stage
3.3.2. Sway Maintaining Stage
3.3.3. Sway Diminishing Stage
4. Discussion and Conclusions
Conclusions of Present Analysis
References
- Silvester, V. Modern Ballroom Dancing: History and Practice; Barrie and Jenkins, Ltd.: London, UK, 1977; pp. 1–249. [Google Scholar]
- Moore, A. Ballroom Dancing, 1st ed.; Pitman Publishing Ltd.; A&C Black Publishers Ltd.: London, UK, 2002; pp. 1–308. [Google Scholar]
- Lavelle, D. Latin & American Dances, 1st ed.; A&C Black Publishers Ltd.; Pitman Publishing: London, UK, 1975; pp. 1–194. [Google Scholar]
- ISTD (The Imperial Society of Teachers of Dancing) (Ed.) The Ballroom Technique, 1st ed.; Imperial Society of Teachers of Dancing: London, UK, 1982; pp. 1–134. [Google Scholar]
- ISTD (The Imperial Society of Teachers of Dancing) (Ed.) Viennese Waltz, B. D. C., Recommended Version; Code 105; British Dance Council: London, UK, 2001; pp. 1–8. [Google Scholar]
- Howard, G. The Technique of Ballroom Dancing, 1st ed.; IDTA: Brighton, UK, 1976; pp. 1–131. [Google Scholar]
- Shioya, T. Analysis of Swing Movement in Ballroom Dancing. In Proceedings of the International Sports Engineering Association (ISEA2018), Brisbane, Australia, 26–28 March 2018. [Google Scholar]

Publisher′s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shioya, T. Analysis of Sway in Ballroom Dancing. Proceedings 2018, 2, 223. https://doi.org/10.3390/proceedings2060223
Shioya T. Analysis of Sway in Ballroom Dancing. Proceedings. 2018; 2(6):223. https://doi.org/10.3390/proceedings2060223
Chicago/Turabian StyleShioya, Tadashi. 2018. "Analysis of Sway in Ballroom Dancing" Proceedings 2, no. 6: 223. https://doi.org/10.3390/proceedings2060223
APA StyleShioya, T. (2018). Analysis of Sway in Ballroom Dancing. Proceedings, 2(6), 223. https://doi.org/10.3390/proceedings2060223



