Abstract
A new approach is introduced to evaluate the potential drag reduction by skin suit design in speed sport. The approach relies upon local flow information measured in the wake of a cyclist mannequin. Lagrangian Particle Tracking is employed to measure the distribution of time-average streamwise velocity in a cross-plane of 30 × 100 cm2 behind the stretched leg of the rider at a range of Reynolds numbers (0.4 × 105 < Re < 2.4 × 105). The expected Reynolds number effect is observed: a general wake narrowing at increasing speed. Unexpected local effects are also identified, which may be due to local variations in geometry of the rider’s leg. The conservation of momentum within a control volume containing the leg is used showing that the aerodynamic drag of the rider’s leg can be decreased by application of surface roughness. This outcome is validated by repeated measurements using zigzag tape on the legs’ surface.
1. Introduction
In many speed sports such as cycling, skating and athletics, aerodynamics plays a significant role as reductions of the aerodynamic drag may result in an improved performance of the athlete [1,2]. Aerodynamic drag can be reduced through changes in the posture of the athlete [3] or optimization of his equipment [4]. An alternative approach that has received large attention in the last years is reduction of the aerodynamic drag through optimization of the athlete’s garment.
In speed sports, athletes typically wear skinsuits that are designed with combinations of smooth and rough fabrics, so to affect the flow around the body and reduce the aerodynamic drag. This garment design relies on the concept that the drag coefficient of bluff bodies can be reduced by the application of surface roughness [5] that forces flow transition and postpones separation, yielding the so-called drag crisis. To exploit this concept in the design of skinsuit apparel, conventionally, the torso, head, arms and legs of the human body in cross flow are considered as simplified bluff elements, like cylinders and spheres. Experimental results obtained on these isolated bluff bodies are extrapolated to the human geometry [6,7,8]. This approach, however, neglects the complex human body geometry and flow interactions between the body parts, leaving further drag minimization unexploited.
This work proposes a novel approach that enables the design of low-drag sport garment. Contrary to using drag force data of simplified bluff geometries, the present approach considers the wake flow behind individual parts of the body of the athlete, providing an in-depth insight into local Reynolds number effects and the surface roughness required to minimize the aerodynamic drag.
To assess this approach, Lagrangian Particle Tracking is employed, a flow measurement technique that tracks small tracer particles in the air to obtain quantitative information on the flow field [9]. The measurements are conducted downstream of a cyclist’s leg, where Reynolds number effects are expected to be important due to its bluff geometry. It is well known that the wake of a bluff body narrows moving from the sub- to super-critical regime and that a reduction of this streamwise velocity in the wake is associated with a drag reduction [10]. The streamwise velocity in the wake is considered to evaluate local drag variations stemming from Reynolds number effects or changes in surface roughness, and to reveal the local drag crisis of the leg only. The measurements are finally repeated with zigzag tape applied on the surface of the leg to validate the approach.
2. Methodology
The aerodynamic drag force acting on an object in relative motion with respect to a fluid can be obtained invoking the conservation of momentum in a control volume containing the object [11]. When considering a sufficient distance behind the model, the downstream pressure recovers to the freestream value and the velocity fluctuations decay [12] such that the time-average drag can be written as the difference between the upstream momentum, , and the wake momentum, :
where is the time-average streamwise velocity, ρ is the fluid density, is the freestream velocity and Sinlet and Swake are, respectively, the upstream and the downstream boundary of the control volume. This expression allows to relate changes in the time-average wake velocity to variations in the drag of the model. In fact, a change in drag between situations 1 and 2 (e.g. different garment applied to the model, or different surface roughness) is obtained using only the delta in the wake momentum assuming unaltered freestream conditions:
Hence, the wake momentum is used to evaluate the potential of drag reduction by surface treatment of the model.
3. Experimental Setup and Procedures
3.1. Experimental Setup
The experiments are conducted in the Open Jet Facility (OJF) of the Aerodynamics Laboratories of Delft University of Technology. This low speed wind tunnel has an octagonal cross-section of 2.85 m × 2.85 m with a maximum turbulent intensity of 0.5% of the freestream velocity. The model is a cyclist mannequin manufactured from thermoplastic polyester by additive printing after scanning a professional cyclist in time-trial position [13].
The mannequin is installed on a Giant Trinity Advanced Pro frame (2017 model) supported by four struts (Figure 1-left) fixating the front and rear wheel axis. To trip the boundary layer on the stretched leg, zigzag tape is used with a height of 0.35 mm, a thickness of 11 mm (streamwise direction) and a pitch of 6 mm, which is applied at both sides of the leg at approximately 45 degrees from the most upstream surface position (Figure 1-right).

Figure 1.
Cyclist and HFSB seeding system (left) and the application of zigzag tape on the stretched leg (right).
Lagrangian Particle Tracking measurements are conducted about 20 cm behind the stretched leg of the mannequin (Figure 2), with and without the application of zigzag tape, in a range of velocities between 4 and 24 m/s (Re = 0.4 × 105 to 2.4 × 105 based on the average leg thickness). Helium-filled soap bubbles (HFSB) are used as flow tracers, which are injected into the flow by four aerodynamically shaped rakes, installed approximately 50 cm upstream of the front-wheel (Figure 1). The HFSB production is controlled through a fluid supply unit provided by LaVision GmbH. Three CMOS cameras (Photron FastCAM SA1, 1 MegaPixel, 12 bit, 20 μm pixel pitch) are used to collect time-resolved images in short bursts of 11 frames allowing to reconstruct short particle tracks in the 5 cm thick volume illuminated by a Continuum Mesa PIV 532-120-M Nd:YAG laser (pulse energy of 18 mJ at 1 kHz). Three cameras are located at x = 200 cm; y = −40, 15, 70 cm; z = 180 cm and are equipped with 50 mm objectives, apertures set to f/4, and the sensors cropped to 512 × 1024 pixels. The acquisition frequency is in the range of 1–6 kHz increasing with increasing freestream velocity. An area of 30 cm × 100 cm is seeded with HFSB by traversing the seeding system into two different positions in height, where in each position 500 bursts of 11 images are acquired at 10 Hz. Image acquisition and processing are conducted with the DaVis 8.4 software from LaVision GmbH.
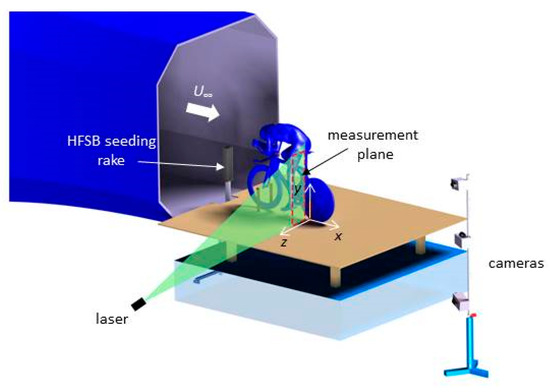
Figure 2.
Illustration of the experimental setup.
3.2. Data Reduction
The Shake-The-Box (STB) [14] is employed to obtain particle tracks from the 500 bursts of 11 time-resolved images after average intensity subtraction to eliminate background reflections. The Lagrangian particle tracks obtained over the two seeder positions are integrated into a single volume before the scattered velocity information is mapped onto a Cartesian grid with bins of 5 × 3 × 3 cm3 and an overlap of zero, 0.75 and 0.75 in x, y and z-direction, respectively. The normalized uncertainty associated with the resulting time-average velocity, is obtained at 95% confidence level: , with N being the amount of individual particles per bin and the standard deviation of the velocity distribution. The latter contains both the physical velocity fluctuations and the error in the PTV velocity, which is assumed to contain a random component only. Bins with less than 50 particles are considered too sparse and not used for the computation of the velocity statistics. Finally the time-average velocity fields are normalized by the corresponding freestream velocity to compare the wake flow at different Reynolds numbers.
4. Results
4.1. Effect of Reynolds Number
The time-average velocity field behind isolated bluff bodies changes significantly going from the sub- to the super-critical regime [10]; in particular, the wake narrows and the area of reverse flow becomes smaller. As it can also be deduced from Equation (1), these flow field characteristics behind the model correspond to a decrease in aerodynamic drag. Figure 3 presents the distribution of the non-dimensional time-average streamwise velocity behind the stretched leg of the mannequin at 4.2, 6.2, 12.4, 16.4 and 23.3 m/s. It is observed that the velocity distribution behind the leg significantly changes along the y-coordinate; at the lowest speed, the wake is wider and high velocity deficit appears behind the thighs, knees and the foot (e.g., Figure 3-left). In between these areas, the wake is narrower. Furthermore, in all five cases the velocity reaches freestream conditions at the left boundary of the domain. Besides the similarities, the velocity distributions can be distinguished by an overall narrowing of the wake with increasing freestream velocity.
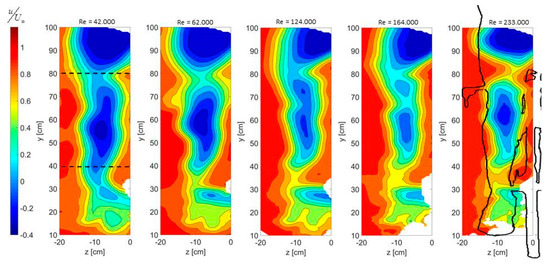
Figure 3.
Spatial distribution of non-dimensional time-average streamwise velocity at increasing freestream velocity. The contour of the mannequin is included at Re = 233.000 only for better readability.
The uncertainty of the time-average non-dimensional velocity increases with increasing freestream velocity due to a decreasing seeding concentration at higher speeds. At = 23.3 m/s the uncertainty remains below 0.5% in the freestream region, while in the wake it shows peak values of 2%. Only in the wake of the foot (y < 30 cm) the uncertainty reaches 5% due to the relatively low seeding concentration.
To better understand how Reynolds number effects vary with the geometry of the leg, profiles of streamwise velocity along the z-axis at two different heights, y = 40 cm and y = 80 cm (indicated in Figure 3-left) are compared in Figure 4. At the height of the calf (Figure 4-left) the wake narrows with increasing Reynolds number until Re = 164.000 after which is remains relatively unaltered. At the height of the upper leg (Figure 4-right), instead, the most significant change in the streamwise velocity is observed between Re = 164.000 and Re = 233.000, which is rather unexpected. The opposite is expected based on Reynolds number effects in the wake of two-dimensional cylinder: the narrowing of the wake flow behind a thin cylinder occurs at higher Reynolds number then that behind a thick cylinder. This suggests that the knowledge obtained from isolated two-dimensional bluff geometries may not directly be extrapolated to more complex geometries, such as the human leg, and that measurements on the actual athlete, such as those presented in this work, are needed for future drag minimization.
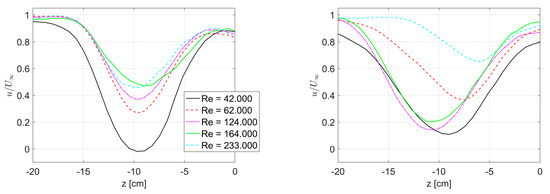
Figure 4.
Profiles of non-dimensional time-average streamwise velocity along the z-axis at y = 40 cm (left) and y = 80 cm (right).
To analyze how the changes in wake velocity affect the aerodynamic drag of the leg, the time-average momentum through the wake plane is computed. An increase of the momentum in the downstream plane of the leg due to changes in the Reynolds number indicates a decrease of aerodynamic drag coefficient of the leg (Equation (1)). Figure 5 presents the negative normalized time-average streamwise momentum, −CM in the downstream plane of the leg, 10 < y < 100; −20 < z < 0, that contains velocity data in all Reynolds number cases. The wake momentum, Mwake (Equation (1)) is normalized as with q being the dynamic pressure. The decreasing trend of negative normalized momentum matches well the drag crisis of an isolated two-dimensional cylinder [5], confirming the solidity of the measurement principle. It is observed that the point of minimum negative momentum is not reached. This suggests that the aerodynamic drag of the leg can be decreased by the application of surface roughness throughout the entire range of Reynolds numbers.
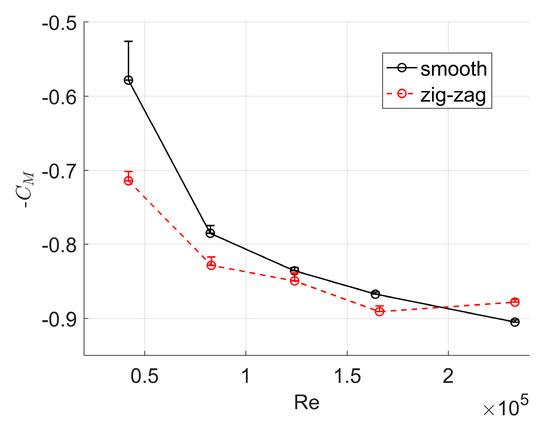
Figure 5.
Negative normalized time-average streamwise momentum through the plane in the wake of the stretched leg dressed time-trial apparel (black solid line) and with zigzag tape (red dashed line).
The uncertainty in CM stemming from the uncertainty in the measured streamwise velocity is within 0.1% and is neglected. Instead, an error is introduced underestimating CM when Swake is narrower than the wake of the leg. This uncertainty, depicted by the error bars in Figure 5, is more pronounced at the lower Reynolds numbers, where a wider wake is observed (e.g., black line in Figure 4-right) and, therefore, does not affect the trend in the negative wake momentum.
4.2. Effect of Surface Roughness Elements
The velocity measurements in the wake of the leg are repeated with zigzag tape applied (see Figure 1). The choice for the zigzag tape is not to minimize drag, for which another kind of surface roughness may be better suited. Instead the zigzag tape is known to be a rather effective instrument for passive flow control by forcing the transition of the boundary layer from the laminar to the turbulent regime [15].
The negative streamwise momentum in the wake of the leg with zigzag tape is consistently reduced with respect to that of the smooth leg up to Re~200.000 (Figure 5-red dashed line) showing that the drag of the leg can be decreased by the application of zigzag tape. This validates that the proposed technique based on the local momentum analysis can be used to predict possible drag reductions. In fact, further optimization may be possible using further localized information, such as the velocity profiles presented in Figure 4, and locally applying different roughness types.
5. Conclusions
Lagrangian Particle Tracking measurements are conducted in the wake of the leg of a cyclist mannequin. The distribution of streamwise velocity behind the leg shows a clear wake narrowing with increasing Reynolds number, indicating a reduction of the drag coefficient. This drag reduction is quantified computing the negative normalized momentum in the wake plane. The decreasing trend of the momentum indicates that drag reductions of the leg are possible up to 22 m/s, which is well above typical time-trial speeds. Repeated measurements with zigzag tape applied on the leg show that the drag of the leg is indeed reduced, thus validating the use of local flow information to predict possible drag reductions. Finally, locally (around the calf and upper leg) unexpected Reynolds number effects are observed, which may be exploited in future drag minimization.
Acknowledgments
Yash Shah is acknowledged for his support during the experiments.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sætran, L.; Oggiano, L. Skin suit aerodynamics in speed skating. In Sport Aerodynamics; Nørstrud, H., Ed.; CISM International Centre for Mechanical Sciences: Springer, Vienna, 2008. [Google Scholar]
- Gibertini, G.; Grassi, D. Cycling Aerodynamics. In Sport Aerodynamics; Nørstrud, H., Ed.; CISM International Centre for Mechanical Sciences: Springer, Vienna, 2008. [Google Scholar]
- Defraeye, T.; Blocken, B.; Koninckx, E.; Hespel, P.; Carmeliet, J. Aerodynamic study of different cyclist positions: CFD analysis and full-scale wind-tunnel test. J. Biomech. 2010, 43, 1262–1268. [Google Scholar] [CrossRef] [PubMed]
- Zdravkovich, M.M. Aerodynamics of bicycle wheel and frame. J. Wind Eng. Ind. Aerodyn. 1992, 40, 55–70. [Google Scholar] [CrossRef]
- Achenbach, E.; Heinecke, E. On vortex shedding from smooth and rough cylinders in the range of Reynolds numbers 6 × 103 to 5 × 106. J. Fluid Mech. 1981, 109, 239–251. [Google Scholar] [CrossRef]
- Brownlie, L.; Kyle, C.; Carbo, J.; Demarest, N.; Harber, E.; MacDonald, R.; Nordstrom, M. Streamlining the time trial apparel of cyclists: The Nike Swift Spin project. Sports Technol. 2009, 2, 53–60. [Google Scholar] [CrossRef]
- Oggiano, L.; Brownlie, L.; Troynikov, O.; Bardal, L.M.; Sæter, C.; Sætran, L. A review on skin suits and sport garment aerodynamics: Guidelines and state of the art. Procedia Eng. 2013, 60, 91–98. [Google Scholar] [CrossRef]
- Spurkland, L.; Bardal, L.M.; Sætran, L.; Oggiano, L. Low Aerodynamic Drag Suit for Cycling—Design and Testing. In Proceedings of the 3rd icSPORTS, Lisbon, Portugal, 15–17 November 2015; pp. 89–96. [Google Scholar]
- Raffel, M.; Willert, C.E.; Wereley, S.T.; Kompenhans, J. Particle Image Velocimetry—A Practical Guide, 2nd ed.; Berlin Springer: Berlin, Germany, 2007. [Google Scholar]
- Terra, W.; Sciacchitano, A.; Scarano, F. Drag analysis from PIV data in speed sport. Procedia Eng. 2016, 147, 50–55. [Google Scholar] [CrossRef]
- Anderson, J.D., Jr. Fundamentals of Aerodynamics; McGraw-Hill: New York, NY, USA, 1991. [Google Scholar]
- Terra, W.; Sciacchitano, A.; Scarano, F. Aerodynamic drag of a transiting sphere by large-scale tomographic-PIV. Exp. Fluids 2017. [Google Scholar] [CrossRef]
- Van Tubergen, J.; Verlinden, J.; Stroober, M.; Baldewsing, R. Suited for performance: Fast full-scale replica of athlete with FDM. In Proceedings of the SCF’17, Cambridge, MA, USA, 12–13 June 2017. [Google Scholar]
- Schanz, D.; Gesemann, S.; Schröder, A. Shake-The-Box: Lagrangian particle tracking at high particle densities. Exp. Fluids 2016, 57, 70. [Google Scholar] [CrossRef]
- Van Rooij, R.P.J.O.M.; Timmer, W.A. Roughness Sensitivity Considerations for Thick Rotor Blade Airfoils. J. Sol. Energy Eng. 2003, 125, 468–478. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).