Information Entropy of Molecular Tunneling ^†

Abstract

Molecular tunneling process has been considered by means of radiation theory. The formula for information entropy calculation has been derived by means of interaction model of thermal equilibrium radiation with a molecule at low temperatures. The physical meaning of information entropy for low-temperature plateau of unimolecular chemical reaction has been determined. It is a measure of conversion of thermal radiation energy to mechanical energy that moves atoms in a molecule during elementary activation act. It is also a measure of uncertainty of this energy conversion. The conversion takes place at a temperature when the average energy of the elementary activation act is equal to a part of zero energy of the transforming molecule. Two unimolecular reactions have been investigated. These are Fe-CO bond recombination in β-hemoglobin and double proton transfer in benzoic acid dimer for sequential deuteration of hydrogen bond and various hydrostatic pressures. Using the information entropy formula it is possible to calculate its value in energy units of measurements for low-temperature plateau. Probabilities of occurrence of the reactions under considerations, their efficiency and mean-square fluctuations of the distribution function parameters have also been determined.

1. Introduction

The activation process model was proposed in 1990 [1], its physical nature being alternative to the well-known Boltzmann-Arrhenius model. As a result of its development, the interaction model of thermal equilibrium radiation with a molecule at low temperatures was created in 2002 to explain such a puzzling process as molecular tunneling [2]. The interaction process was caused by subsequent realization of the molecule’s sub-conformations. Each sub-conformation state was approximated by means of a harmonic quantum oscillator. The oscillator was considered non-ideal, i.e., its degeneracy and exclusion of some excited vibration levels was taken into account. The molecular tunneling itself was due to a part of the oscillator’s zero energy, the energy being the result of the transition from the previous sub-conformation state to the next one. All the process features were allowed for while choosing the distribution function parameters. This made possible a numerical simulation of four molecular tunneling reactions. These were photoinduced conversion of rhodopsin and deuterated rhodopsin into prelumirhodopsin, low-temperature polymerization of formaldehyde, and Fe-CO bond recombination in β-hemoglobin. Information entropy of activation process has been derived recently [3]. Its physical meaning has also been determined. It would be useful to do the same for molecular tunneling process, since several researchers believe that information entropy is conceptually more fundamental even by comparison with energy [4]. So in this paper we derive the formula for information entropy of molecular tunneling. Then two reactions are investigated numerically. These are Fe-CO bond recombination in β-hemoglobin and double proton transfer in benzoic acid dimer. The second reaction is considered for sequential deuteration of hydrogen bond and for various hydrostatic pressures. For all these reactions the values of information entropy are calculated. Probabilities of occurrence of the processes under consideration, their efficiency and mean-square fluctuations of the distribution function parameters are also determined.

2. Information Entropy of Molecular Tunneling

According to the activation process model [5], the activation barrier for molecular tunneling process can be represented as a set of m identical quantum oscillators (Figure 1). These oscillators denote intermediate sub-conformations of a molecule as the latter transforms. The barrier is in thermodynamic equilibrium with the thermal radiation. Any pair of adjacent oscillators has their energy levels shifted by μhν. Here h is Planck constant, μ is the parameter describing the levels shift, and ν is the effective frequency of the quantum oscillator averaged over the generalized reaction coordinate. The value of ν equals to the Einstein spontaneous emission coefficient A [6]. The probability of a transition over this activation barrier can be written as [2]

$$P_{mn\mu }=\frac{e^{-(n+\mu )·mh\nu /kT}·{\Omega }^m[(n+\mu )h\nu ]}{{\displaystyle \sum _{n=0}^{\infty }{e}^{-(n+\mu )·mh\nu /kT}·{\Omega }^m[(n+\mu )h\nu ]}}=\frac{e^{-nmh\nu /kT}·{\Omega }^m[(n+\mu )h\nu ]}{{\displaystyle \sum _{n=0}^{\infty }{e}^{-nmh\nu /kT}·{\Omega }^m[(n+\mu )h\nu ]}}$$

where Ω is the degree of degeneracy for (n + μ) hν vibration level.

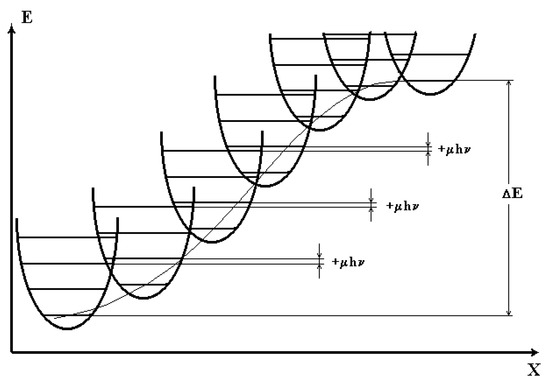
Figure 1. Arrangement of the quantum oscillators averaged over the generalized coordinate of chemical reaction on the potential barrier.

Consequently, information entropy for the process under consideration can be expressed by means of energy units of measurement [3]

$$S_i^{m,\mu }=-k·{\displaystyle \sum _{n=0}^{\infty }\frac{e^{-\frac{mnh\nu }{kT}}·{\Omega }^m[(n+\mu )h\nu ]}{{\displaystyle \sum _{n=0}^{\infty }{e}^{-\frac{mnh\nu }{kT}}·{\Omega }^m[(n+\mu )h\nu ]}}·\ell n\frac{e^{-\frac{mnh\nu }{kT}}·{\Omega }^m[(n+\mu )h\nu ]}{{\displaystyle \sum _{n=0}^{\infty }{e}^{-\frac{mnh\nu }{kT}}·{\Omega }^m[(n+\mu )h\nu ]}}}$$

(1)

Now, let us take into account the fact that different levels (or groups of levels) in the quantum oscillators can have the different degrees of degeneracy, e.g., Ω₁, Ω₂, Ω₃ (Figure 2), i.e., the vibration levels up to quantum number ξ − 1 are non-degenerate, the ones from quantum numbers ξ to η − 1 have the degeneracy Ω₁, and those from η to ζ − 1, Ω₂, and from ζ to ∞, Ω₃ [5,7]. The transition is forbidden if Ω = 0.

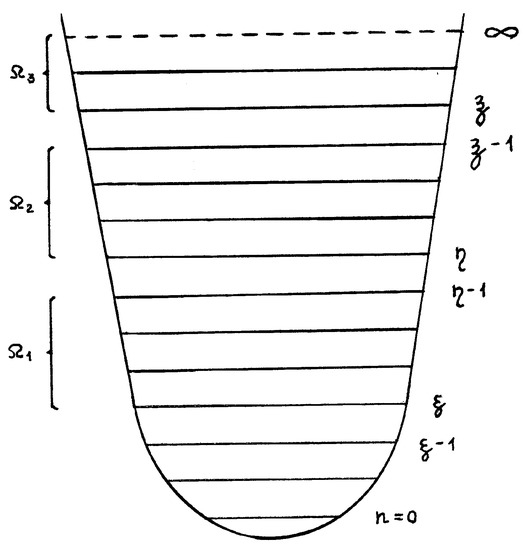
Figure 2. Partition of the energy levels of the averaged quantum oscillator taking into account of the degree of degeneracy (ξ < η < ζ).

Considering the levels partition, the denominator of (1) may be presented as

$$\begin{array}{l}{\displaystyle \sum _{n=0}^{\infty }{e}^{-\frac{mnh\nu }{kT}}·{\Omega }^m[(n+\mu )h\nu ]={\displaystyle \sum _{n=0}^{\xi -1}{e}^{-\frac{mnh\nu }{kT}}}+{\Omega }_1^m[(n+\mu )h\nu ]·}{\displaystyle \sum _{n=\xi }^{\eta -1}{e}^{-\frac{mnh\nu }{kT}}}+\\ +{\Omega }_2^m[(n+\mu )h\nu ]·{\displaystyle \sum _{n=\eta }^{\varsigma -1}{e}^{-\frac{mnh\nu }{kT}}}+{\Omega }_3^m[(n+\mu )h\nu ]·{\displaystyle \sum _{n=\varsigma }^{\infty }{e}^{-\frac{mnh\nu }{kT}}}.\end{array}$$

On the other hand, this denominator can be simplified analytically [2,7]

$${\displaystyle \sum _{n=0}^{\infty }{e}^{-\frac{nmh\nu }{kT}}{\Omega }^m\left[(n+\mu )h\nu \right]}=\frac{1+A·Q^{\xi }+B·Q^{\eta }+C·Q^{\zeta }}{1-Q},$$

where $\begin{array}{ccc}Q=e^{-mh\nu /kT},& A={\Omega }_1^m-1,& B={\Omega }_2^m-{\Omega }_1^m,\end{array}$ and $C={\Omega }_3^m-{\Omega }_2^m$.

So Equation (1) can be transferred into

$$\begin{array}{l}{S}_i^{m,\mu ,\xi ,\eta ,\zeta }=-k·\frac{1-Q}{1+A·Q^{\xi }+B·Q^{\eta }+C·Q^{\zeta }}·\{[{\displaystyle \sum _{n=0}^{\xi -1}{e}^{-\frac{nmh\nu }{kT}}}+{\Omega }_1^m\left[(n+\mu )h\nu \right]·{\displaystyle \sum _{n=\xi }^{\eta -1}{e}^{-\frac{nmh\nu }{kT}}}+\\ +{\Omega }_2^m\left[(n+\mu )h\nu \right]·{\displaystyle \sum _{n=\eta }^{\zeta -1}{e}^{-\frac{nmh\nu }{kT}}}+{\Omega }_3^m\left[(n+\mu )h\nu \right]·{\displaystyle \sum _{n=\zeta }^{\infty }{e}^{-\frac{nmh\nu }{kT}}}]·\ell n[\frac{1-Q}{1+A·Q^{\xi }+B·Q^{\eta }+C·Q^{\zeta }}·\\ ·\left({\displaystyle \sum _{n=0}^{\xi -1}{e}^{-\frac{nmh\nu }{kT}}}+{\Omega }_1^m\left[(n+\mu )h\nu \right]·{\displaystyle \sum _{n=\xi }^{\eta -1}{e}^{-\frac{nmh\nu }{kT}}}+{\Omega }_2^m\left[(n+\mu )h\nu \right]·{\displaystyle \sum _{n=\eta }^{\zeta -1}{e}^{-\frac{nmh\nu }{kT}}}+{\Omega }_3^m\left[(n+\mu )h\nu \right]·{\displaystyle \sum _{n=\zeta }^{\infty }{e}^{-\frac{nmh\nu }{kT}}}\right)]\}.\end{array}$$

(2)

Entropy is additive, so (2) can be separated into four terms:

$$S_i^{m,\mu ,\xi ,\eta ,\zeta }=S_i^{m,\mu ,0\to \xi -1}+S_i^{m,\mu ,\xi \to \eta -1}+S_i^{m,\mu ,\eta \to \zeta -1}+S_i^{m,\mu ,\zeta \to \infty },$$

where

$$S_i^{m,\mu ,0\to \xi -1}=-k·\frac{1-Q}{1+A·Q^{\xi }+B·Q^{\eta }+C·Q^{\zeta }}·{\displaystyle \sum _{n=0}^{\xi -1}{e}^{-\frac{nmh\nu }{kT}}·\ell n\left(\frac{1-Q}{1+A·Q^{\xi }+B·Q^{\eta }+C·Q^{\zeta }}·e^{-\frac{nmh\nu }{kT}}\right)}$$

$$S_i^{m,\mu ,\xi \to \eta -1}=-k·\frac{(1-Q)·{\Omega }_1^m\left[\left(n+\mu \right)h\nu \right]}{1+A·Q^{\xi }+B·Q^{\eta }+C·Q^{\zeta }}·{\displaystyle \sum _{n=\xi }^{\eta -1}{e}^{-\frac{nmh\nu }{kT}}·\ell n\left(\frac{(1-Q)·{\Omega }_1^m\left[\left(n+\mu \right)h\nu \right]}{1+A·Q^{\xi }+B·Q^{\eta }+C·Q^{\zeta }}·e^{-\frac{nmh\nu }{kT}}\right)}$$

$$S_i^{m,\mu ,\eta \to \zeta -1}=-k·\frac{(1-Q)·{\Omega }_2^m\left[\left(n+\mu \right)h\nu \right]}{1+A·Q^{\xi }+B·Q^{\eta }+C·Q^{\zeta }}·{\displaystyle \sum _{n=\eta }^{\zeta -1}{e}^{-\frac{nmh\nu }{kT}}·\ell n\left(\frac{(1-Q)·{\Omega }_2^m\left[\left(n+\mu \right)h\nu \right]}{1+A·Q^{\xi }+B·Q^{\eta }+C·Q^{\zeta }}·e^{-\frac{nmh\nu }{kT}}\right)}$$

$$S_i^{m,\mu ,\zeta \to \infty }=-k·\frac{(1-Q)·{\Omega }_3^m\left[\left(n+\mu \right)h\nu \right]}{1+A·Q^{\xi }+B·Q^{\eta }+C·Q^{\zeta }}·{\displaystyle \sum _{n=\zeta }^{\infty }{e}^{-\frac{nmh\nu }{kT}}·\ell n\left(\frac{(1-Q)·{\Omega }_3^m\left[\left(n+\mu \right)h\nu \right]}{1+A·Q^{\xi }+B·Q^{\eta }+C·Q^{\zeta }}·e^{-\frac{nmh\nu }{kT}}\right)}$$

These four terms can be calculated using the technique described in [3], so we only write the final expression for information entropy:

$$\begin{array}{l}{S}_i^{m,\mu ,\xi ,\eta ,\zeta }=\frac{mh\nu }{T}\left(\frac{Q}{1-Q}+\frac{\xi ·A·Q^{\xi }+\eta ·B·Q^{\eta }+\zeta ·C·Q^{\zeta }}{1+A·Q^{\xi }+B·Q^{\eta }+C·Q^{\zeta }}\right)-k·\ell n\frac{1-Q}{1+A·Q^{\xi }+B·Q^{\eta }+C·Q^{\zeta }}-\\ -k·m·\frac{{\Omega }_1^m·\ell n{\Omega }_1(Q^{\xi }-Q^{\eta })+{\Omega }_2^m·\ell n{\Omega }_2(Q^{\eta }-Q^{\zeta })+{\Omega }_3^m·\ell n{\Omega }_3·Q^{\zeta }}{1+A·Q^{\xi }+B·Q^{\eta }+C·Q^{\zeta }}\end{array}$$

(3)

with $\begin{array}{ccc}Q=e^{-mh\nu /kT},& A={\Omega }_1^m-1,& B={\Omega }_2^m-{\Omega }_1^m,\end{array}$ and $C={\Omega }_3^m-{\Omega }_2^m$.

It should be noted there is no parameter μ responsible for molecular tunneling in (3). Let us try to overcome this apparent misunderstanding in the next section.

3. Information Entropy of Low-Temperature Plateau for Fe-CO Bond Recombination in β-Hemoglobin

Such a process can be simulated with a set of quantum oscillators with non-degenerate vibration levels [2], that is Ω₁ = Ω₂ = Ω₃ = 1. It is the distinctive feature of this reaction that allows one to simplify (3) as

$$S_i^m=\frac{mh\nu }{T}·\frac{Q}{1-Q}-k·\ell n(1-Q)$$

(4)

Equation (4) was derived in the previous paper [3]. By multiplying both parts of (4) into T/m, we get

$$\frac{S_i^m·T}{m}=\frac{h\nu }{e^{\frac{mh\nu }{kT}}-1}-\frac{kT}{m}·\ell n(1-e^{-\frac{mh\nu }{kT}})$$

(5)

The first term of (5) defines the average energy of elementary activation act. The second one describes a measure of energy uncertainty per quantum subsystem, i.e., a molecule’s sub-conformation. It is known from experiments there always exists a temperature of transition from a low-temperature plateau to an activation part for any Arrhenius dependence. Solely from the above reasoning we write the following equality:

$$\frac{h\nu }{e^{\frac{mh\nu }{kT}}-1}=\mu h\nu$$

(6)

Hence the temperature of transition T₁ can be found as

$$T_1=\frac{mh\nu }{k·\ell n(\frac{1}{\mu }+1)}$$

(7)

Information entropy can be expressed in terms of μ only. To do this, we substitute (7) into (5):

$$S_i^{m,\mu }=k·\left[(\mu +1)·\ell n(1+\mu )-\mu ·\ell n\mu \right].$$

(8)

The following values of the parameters for the reaction under consideration can be used: ν = 3.3·10⁶ Hz, m = 9.0 × 10⁵, μ = 1.8·10⁶, h = 6626 × 10⁻³⁴ J s, and k = 1381 × 10⁻²³ J/K [2]. Insertion of these values into (7) gives T₁ = 10.776 K. Now it is possible to calculate the value of information entropy for the beginning of activation part of experimental Arrhenius dependence. To do this, we substitute the value of T₁ into (4) to get S_i^m = 3.536 × 10⁻²⁸ J/K.

It should be noted that entropy S_i^m is measured in energy units. On the other hand, (8) gives the value of information entropy for the low-temperature plateau $S_i^{m,\mu }$ = 3.536 × 10⁻²⁸ J/K. Comparison of the two values shows that S_i^m is the required parameter corresponding to the low-temperature plateau.

Notice that T₁ is approximately equal to the temperature of activation barrier creation T_m = 10.397 K [8]. Besides, Laura Eisenstein found experimentally that a chemical reaction rate constant of Fe-CO bond recombination in β-hemoglobin is temperature independent for temperatures lower than 10 K [9]. All things considered, the interaction model of thermal equilibrium radiation with a molecule at low temperatures is realistic for molecular tunneling representation. So we have examined the ideal example of molecular tunneling reaction, i.e., when an activation barrier can be represented as a set of oscillators with non-degenerate vibration levels. Let us consider another reaction where the degeneracy and exclusion of some excited vibration levels will be taken into account.

4. Information Entropy of the Double Proton Transfer in the Benzoic Acid Dimer

This process was numerically simulated in [5]. The following formula for the average energy of the elementary activation act was used:

$${\overline{\epsilon }}_m^{\xi ,\eta ,\zeta ,\mu }=h\nu ·\left(\frac{Q}{1-Q}+\frac{\xi ·A·Q^{\xi }+\eta ·B·Q^{\eta }+\zeta ·C·Q^{\zeta }}{1+A·Q^{\xi }+B·Q^{\eta }+C·Q^{\zeta }}+\mu \right)$$

(9)

By analogy with (6) we can write a transcendental equation:

$$h\nu ·\left(\frac{Q}{1-Q}+\frac{\xi ·A·Q^{\xi }+\eta ·B·Q^{\eta }+\zeta ·C·Q^{\zeta }}{1+A·Q^{\xi }+B·Q^{\eta }+C·Q^{\zeta }}\right)=\mu h\nu$$

(10)

One has to solve (10) numerically to get the temperature of transition T₁ from the low-temperature plateau to the activation part of Arrhenius dependence. Substitution of T₁ into (3) gives the value of information entropy for the low-temperature plateau of the process under consideration.

Experimental studies of the temperature dependence of the chemical reaction rate constant were made for monocrystalline simples with sequential deuteration of hydrogen bonds [10] and polycrystalline ones under various hydrostatic pressures [11].

4.1. Sequential Deuteration of the Hydrogen Bond

4.1.1. Information Entropy of the Low-Temperature Plateau

Numerical simulation of this process showed the parameters Ω₃ and ζ are excess [5]. So (10) can be rewritten as

$$h\nu ·\left(\frac{Q}{1-Q}+\frac{\xi ·A·Q^{\xi }+\eta ·B·Q^{\eta }}{1+A·Q^{\xi }+B·Q^{\eta }}\right)=\mu h\nu$$

(11)

The calculated values of T₁ can be found in Table 1.

Table 1. Information entropy for partial and complete deuteration of the hydrogen bond in the benzoic acid dimer.

Bond	H-H	D-H	D-D
$\nu ·{10}^9$ Hz	8.4	5.0	1.6
m	23	43	247
Ω1	0.75	0.80	0.95
Ω2	1.0	1.0	1.0
ξ	1.0	1.0	1.0
η	177	170	90
μ	4.897 × 10−2	3.0 × 10−3	1.013 × 10−3
T1, K	56.371	68.587	125.757
Sim,ξ,η, J/K	8.907 × 10−25	6.753 × 10−26	5.881 × 10−27
Sim,μ, J/K	2.732 × 10−24	2.821 × 10−25	1.104 × 10−25

Equation (3) may be simplified here because $\ell n{\Omega }_2=0$:

$$\begin{array}{l}{S}_i^{m,\xi ,\eta }=\frac{mh\nu }{T}\left(\frac{Q}{1-Q}+\frac{\xi ·A·Q^{\xi }+\eta ·B·Q^{\eta }}{1+A·Q^{\xi }+B·Q^{\eta }}\right)-k·\ell n\frac{1-Q}{1+A·Q^{\xi }+B·Q^{\eta }}-\\ -k·m·\frac{{\Omega }_1^m·\ell n{\Omega }_1(Q^{\xi }-Q^{\eta })}{1+A·Q^{\xi }+B·Q^{\eta }}\end{array}$$

(12)

The derived values of information entropy are shown in Table 1.

Now let us return to the ideal set of oscillators with non-degenerate vibration levels. This set is a simplification for our deuteration process, but we can use (8) to get the values of $S_i^{m,\mu }$ and compare them with those of $S_i^{m,\xi ,\eta }$. As seen from Table 1, $S_i^{m,\xi ,\eta }$ are 3–20 times smaller than $S_i^{m,\mu }$. This result can be reasonably expected.

4.1.2. Assumptions Needed for Calculation of the Required Parameters

To calculate probabilities of occurrence of the reactions under consideration as well as their efficiency and mean-square fluctuations of the entropy parameters, one has to know two temperatures [3]. These are the temperature of activation barrier creation T_m and the temperature T₂ when the barrier is overcome by absorbing only two quanta of thermal equilibrium radiation (TER). These temperatures were derived analytically for the set of ideal quantum oscillators [8]. The corresponding activation barrier was in quasi-equilibrium with TER. Temperature independent Einstein coefficients A and B were used to get the values of T₂ and T_m. However, these coefficients depend on temperature in our case, so it is not possible to write down a set of equations that satisfy the Einstein detailed balancing principle for a molecule interacting with TER. One has to invoke some other assumptions to calculate T_m and T₂. Such assumptions must not be contradictory to a physical meaning of the activation process model.

It has just been found in Section 3, that T_m is approximately equal to T₁ (T_m = 10,391 K vs. T₁ = 10,776 K), where T₁ is the temperature of transition from the low-temperature plateau to the activation part for the Arrhenius dependence of Fe-CO bond-recombination in β-hemoglobin. Let us assume that T₁ is the temperature of activation barrier creation if the barrier consists of non-ideal quantum oscillators. Of course, this assumption requires a more rigorous proof. Nevertheless, we can state that at T₁ the activation barrier begins to manifest itself by defining the chemical reaction rate constant of the process under consideration.

To get the value of T₂, the following reasonings must be taken into account. First, as the molecule under transformation is in thermodynamic quasi-equilibrium with TER, its probability of transformation should be slightly less or greater than 0.5 [3]. Second, mean-square fluctuations of the distribution function parameters must be less than parameter values themselves, for the distribution function has no physical meaning otherwise.

So the change of information entropy of activation that defines the experimental Arrhenius dependence can be derived using (12):

$$\Delta S_i^{m,\xi ,\eta }=S_{i{T}_1}^{m,\xi ,\eta }-S_{i{T}_2}^{m,\xi ,\eta }$$

(13)

Suppose that a unimolecular reaction is a large thermodynamic equilibrium fluctuation. Then we can calculate its probability of occurrence using Einstein Formula [12,13]

$$W=e^{\frac{\Delta S_i^{m,\xi ,\eta }}{k}}$$

(14)

To get a unimolecular reaction efficiency, both left-hand and right-hand sides of (12) should be multiplied by T/m

$$\begin{array}{l}{S}_i^{m,\xi ,\eta }·\frac{T}{m}=h\nu \left(\frac{Q}{1-Q}+\frac{\xi ·A·Q^{\xi }+\eta ·B·Q^{\eta }}{1+A·Q^{\xi }+B·Q^{\eta }}\right)-\frac{kT}{m}·\ell n\frac{1-Q}{1+A·Q^{\xi }+B·Q^{\eta }}-\\ -k·T·\frac{{\Omega }_1^m·\ell n{\Omega }_1(Q^{\xi }-Q^{\eta })}{1+A·Q^{\xi }+B·Q^{\eta }}\end{array}$$

(15)

The first term of the right-hand side of (15) is the average energy of the elementary activation act [3,5]. The two other terms describe uncertainty of this energy. The uncertainty is due to unevenness and fuzziness of the distribution function representing the activation process. If the left-hand side of (15) is taken to be 100%, a unimolecular reaction efficiency can be easily calculated.

So if a unimolecular reaction can be represented as a large fluctuation, then information entropy change $\Delta S_i^{m,\xi ,\eta }$ is a consequence of this fluctuation. Knowing $\Delta S_i^{m,\xi ,\eta }$ one can get mean-square relative fluctuations of the entropy parameters. The following formula proposed by Einstein [12] can be used

$$\overline{{\Delta }^2}=\frac{k}{(\overline{-\frac{{\partial }^2\Delta S_i^{m,\xi ,\eta }}{{\partial }^2\Delta }})}$$

(16)

where Δ is one of the parameters that determines the entropy change as a result of the fluctuation.

4.1.3. Calculation Results

The results are summarized in Table 2 and Table 3.

Table 2. Parameters for sequential deuteration of the hydrogen bond in the benzoic acid dimer.

Bond	H-H	D-H	D-D
ν (Hz)	8.4 × 109	5.0 × 109	1.6 × 109
m	23	43	247
νa (Hz)	1.932 × 1011	2.15 × 1011	3.952 × 1011
Ώ1	0.75	0.8	0.95
Ώ2	1.0	1.0	1.0
ξ	1.0	1.0	1.0
η	177	170	90
T1	56.371	68.587	125.757
T2	258	297.4	324
W	0.546	0.546	0.546
$\sqrt{\overline{\Delta {\nu }^2}}$ (Hz)	2.274 × 109	1.203 × 109	4.285 × 108
$\sqrt{\overline{\Delta m^2}}$	5.147	10.04	66.029
$\sqrt{\overline{\Delta {\nu }_a{}^2}}$ (Hz)	5.23 × 1010	5.175 × 1010	1.058 × 1011
$m·\sqrt{\overline{\Delta {\nu }^2}}$ (Hz)	5.23 × 1010	5.175 × 1010	1.058 × 1011
$\nu ·\sqrt{\overline{\Delta m^2}}$ (Hz)	4.324 × 1010	5.02 × 1010	1.057 × 1011
$\sqrt{\overline{\Delta {\Omega }_1{}^2}}$	0.09	0.172	0.212
$\sqrt{\overline{\Delta {\Omega }_2{}^2}}$	0.079	0.034	0.006
$\sqrt{\overline{\Delta {\xi }^2}}$	0.994	0.985	0.995
$\sqrt{\overline{\Delta {\eta }^2}}$	57.593	49.941	30.233

Table 3. Comparison of the average energy of the elementary activation act and its uncertainty for sequential deuteration of the hydrogen bond.

Bond	H-H		D-H		D-D
Temperature, K	T1	T2	T1	T2	T1	T2
	56.371	258	68.587	297.4	125.757	324
$\overline{{\epsilon }_m}$ (%)	12.458	54.515	9.228	84.216	35.851	85.575
$(S_i·T)/m-\overline{{\epsilon }_m}$ (%)	87.542	45.484	90.772	15.784	64.149	14.425

In Table 2 ${\nu }_a=m\nu$ is the effective activation frequency. As seen from the results, there exists a correlation between $\Delta {\nu }_a$ and $\Delta \nu$. The correlation can be written as $\sqrt{{(\Delta {\nu }_a)}^2}=m·\sqrt{{(\Delta \nu )}^2}.$ When calculating T₂ and W, the results turn out to be very sensitive to ξ. This parameter describes the lowest vibration level of harmonic oscillator where a quantum sub-conformation of the transforming molecule can be called non-ideal.

Table 3 demonstrates the efficiency of the reactions under consideration.

As temperature increases, so does the reaction efficiency. This result is somewhat unexpected, since the temperature dependence of Fe-CO bond recombination in β-hemoglobin was shown to be just the opposite [3].

When the results of Table 3 are compared with those of Table 4, it is apparent that a unimolecular reaction efficiency increases with increasing temperature if the reaction is represented as a set of non-ideal quantum oscillators.

Table 4. Reaction efficiency of Fe-CO bond recombination in β-hemoglobin for various temperatures.

Process	Fe-CO Recombination
Temperature, K	T1	T2
	10.397	80.862
$\overline{{\epsilon }_m}$ (%)	93.202	63.981
$(S_i^m·T)/m-\overline{{\epsilon }_m}$ (%)	6.798	34.019

4.2. Information Entropy of the Double Proton Transfer in the Polycrystalline Benzoic Acid Sample under Various Hydrostatic Pressures

As in the previous section, the activation barrier can be represented as a set of ideal or non-ideal quantum oscillators. The corresponding values of information entropy for low-temperature plateaus are given in Table 5. It can be easily seen that $S_i^{m,\xi ,\eta }$ are 2–3 times smaller than $S_i^{m,\mu }$.

Table 5. Information entropy of the double proton transfer in the polycrystalline benzoic acid sample under various hydrostatic pressures.

Pressure, kbar	0.0	1.3	2.0	2.4	2.9	3.3
$\nu ·{10}^9$ Hz	8.4	8.9	9.4	9.9	10.4	10.9
m	44	42	40	38	36	34
Ω1	1.86	0.86	0.88	0.89	0.88	0.87
Ω2	1.0	1.0	1.0	1.0	1.0	1.0
ξ	1.0	1.0	1.0	1.0	1.0	1.0
η	77	77	77	77	77	77
μ	3.452 × 10−2	5.955 × 10−2	1.223 × 10−1	1.616 × 10−1	2.115 × 10−1	2.991 × 10−1
T1, K	91.217	103.808	82.515	67.925	84.384	106.162
Sim,ξ,η, J/K	7.335 × 10−25	1.086 × 10−24	2.401 × 10−24	3.430 × 10−24	3.771 × 10−24	4.345 × 10−24
Sim,μ, J/K	2.089 × 10−24	3.166 × 10−24	7.746 × 10−24	6.469 × 10−24	7.746 × 10−24	9.678 × 10−24

Square roots of mean-square relative fluctuations of the distribution function parameters are shown in Table 6. Once again, there is a correlation between the effective activation frequency ${\nu }_a$ and oscillator frequency $\nu$. It can be written as

$$\sqrt{\overline{\Delta {\nu }_a^2}}=m·\sqrt{\overline{\Delta {\nu }^2}}$$

Table 6. Parameters for the double proton transfer in the polycrystalline benzoic acid dimer under various hydrostatic pressures.

Pressure, kbar	0.0	1.3	2.0	2.4	2.9	3.3
ν 109. Hz	8.4	8.9	9.4	9.9	10.4	10.9
m	44	42	40	38	36	34
νa 1011, Hz	3.696	3.738	3.76	3.762	3.744	3.706
Ω1	0.86	0.86	0.88	0.89	0.88	0.87
Ω2	1.0	1.0	1.0	1.0	1.0	1.0
ξ	1.0	1.0	1.0	1.0	1.0	1.0
η	77	77	77	77	77	77
T1	91.217	103.808	82.515	67.925	84.384	106.162
T2	260	265	246.9	225.7	239.9	251.65
W	0.539	0.52	0.51	0.476	0.472	0.46
$\sqrt{\overline{\Delta {\nu }^2}}$ × 109, Hz	2.412	2.563	3.07	3.848	3.657	3.586
$\sqrt{\overline{\Delta m^2}}$	11.621	11.208	11.239	11.991	11.195	10.837
$\sqrt{\overline{\Delta {\nu }_a{}^2}}$ × 1011 (Hz)	1.061	1.076	1.228	1.463	1.317	1.219
$m·\sqrt{\overline{\Delta {\nu }^2}}$ × 1011 (Hz)	1.061	1.076	1.228	1.463	1.317	1.219
$\nu ·\sqrt{\overline{\Delta m^2}}$ × 1011 (Hz)	0.976	0.998	1.057	1.187	1.164	1.181
$\sqrt{\overline{\Delta {\Omega }_1{}^2}}$	0.082	0.081	0.059	0.057	0.066	0.08
$\sqrt{\overline{\Delta {\Omega }_2{}^2}}$	0.036	0.037	0.048	0.066	0.058	0.053
$\sqrt{\overline{\Delta {\xi }^2}}$	0.999	0.983	0.999	0.999	0.999	0.999
$\sqrt{\overline{\Delta {\eta }^2}}$	27.67	27.788	30.947	36.823	33.158	31.085

The value of $\xi$ is still extremely important when calculating T₂ and W.

The reaction probability decreases with increasing hydrostatic pressure applied to the sample. The pressure dependence is attributable to the departure of the thermodynamic system under consideration from the equilibrium state, so that the probability is less than 0.5.

Once again, as temperature increases, so does the reaction efficiency (Table 7).

Table 7. Comparison of the average energy of the elementary activation act and its uncertainty for various hydrostatic pressures applied to the sample.

Pressure, kbar	Temperature, K		$\overline{{\mathit{\epsilon }}_{\mathit{m}}}$ (%)	$({\mathit{S}}_{\mathit{i}}^{\mathit{m}}·\mathit{T})/\mathit{m}-\overline{{\mathit{\epsilon }}_{\mathit{m}}}$ (%)
0,0	T1	91.217	12.636	87.364
	T2	260	62.461	30.54
1,3	T1	103.808	13.081	86.919
	T2	265	66.353	33.647
2,0	T1	82.515	15.382	84.618
	T2	246.9	43.447	56.553
2,4	T1	67.925	17.29	82.71
	T2	225.7	29.528	70.472
2,9	T1	84.384	16.491	83.509
	T2	239.9	35.22	64.78
3,3	T1	106.161	15.924	84.076
	T2	251.65	40.836	59.164

4.3. Calculation of Ratios between Mean Square Relative Fluctuations of the Distribution Function Parameters and the Parameters Themselves

The calculated ratio values for the two reactions of interest are shown in Table 8 and Table 9.

Table 8. Square roots of mean-square relative fluctuations of the distribution function parameters divided by the according parameters (in percent).

Bond	H-H	D-H	D-D
$\sqrt{\overline{\Delta {\nu }^2}}/\nu$ (%)	27.07	24.068	26.781
$\sqrt{\overline{\Delta m^2}}/m$ (%)	22.379	23.349	26.732
$\sqrt{\overline{\Delta {\nu }_a{}^2}}/{\nu }_a$ (%)	27.069	24.068	26.781
$\sqrt{\overline{\Delta {\Omega }_1{}^2}}/{\Omega }_1$ (%)	11.976	21.519	22.274
$\sqrt{\overline{\Delta {\Omega }_2{}^2}}/{\Omega }_2$ (%)	7.873	3.436	0.591
$\sqrt{\overline{\Delta {\xi }^2}}/\xi$ (%)	99.429	98.531	99.516
$\sqrt{\overline{\Delta {\eta }^2}}/\eta$ (%)	32.539	29.377	33.592

Table 9. Square roots of mean-square relative fluctuations of the distribution function parameters divided by the according parameters (in percent).

Pressure, kbar	0.0	1.3	2.0	2.4	2.9	3.3
$\sqrt{\overline{\Delta {\nu }^2}}/\nu$ (%)	28.714	28.796	32.654	38.878	35.162	32.895
$\sqrt{\overline{\Delta m^2}}/m$ (%)	26.412	26.686	28.098	31.554	31.096	31.874
$\sqrt{\overline{\Delta {\nu }_a{}^2}}/{\nu }_a$ (%)	28.714	28.796	32.654	38.878	35.162	32.895
$\sqrt{\overline{\Delta {\Omega }_1{}^2}}/{\Omega }_1$ (%)	9.554	9.467	6.715	6.593	7.536	9.164
$\sqrt{\overline{\Delta {\Omega }_2{}^2}}/{\Omega }_2$ (%)	3.572	3.711	4.756	6.597	5.799	5.344
$\sqrt{\overline{\Delta {\xi }^2}}/\xi$ (%)	99.881	98.311	99.973	99.992	99.986	99.995
$\sqrt{\overline{\Delta {\eta }^2}}/\eta$ (%)	35.935	36.089	40.191	47.823	43.063	40.371

It was shown earlier [3] that if the activation barrier is represented as a set of ideal quantum oscillators then all the three parameters ν, m and ν_a have equal effect on the large thermodynamic fluctuation, since their appropriate ratios are all about 93%. As the data of Table 8 and Table 9 suggest, the situation is different for non-ideal quantum oscillators set. The model parameters do not influence the thermodynamic fluctuation to the same extent.

Particular attention should be given to the degeneracies Ω₁ and Ω₂. Their minor change of several percent will give rise to the large thermodynamic fluctuation responsible for unimolecular reaction progress.

5. Conclusions

Molecular tunneling is one of the most interesting and yet little-known low-temperature chemical processes. This is mainly because a tunneling molecule mass is three orders of magnitude greater than that of electron, so its de Broglie wavelength is small compared to a chemical bond length. Since this process occurs widely in nature, its investigation is a fundamental problem. The proposed interaction model of thermal equilibrium radiation with a molecule at low temperatures describes the process by using a distribution function. The function represents an activation barrier as the molecule’s sub-conformation states set. All the states share a common trait, that of providing the tunneling process by means of a part of zero-point vibrations energy.

To study the molecular tunneling process in more detail a concept of information entropy for activation process has been used. Its physical meaning was determined earlier [2]. The results of this investigation can be summarized as follows:

• The formula for information entropy of molecular tunneling has been derived.
• Arrhenius dependence for molecular tunneling process is caused by information entropy change. In addition, information entropies for low-temperature plateau and for the beginning of the activation part of Arrhenius dependence are equal.
• Probability of occurrence of the double proton transfer in the benzoic acid dimer has been calculated for sequential deuteration of the hydrogen bond and various hydrostatic pressures.
• Efficiency comparison has been made for Fe-CO bond recombination in β-hemoglobin and double proton transfer in benzoic acid dimer. The first reaction is more effective at low temperatures, while the temperature dependence of the second one is the opposite.
• There exists a correlation between mean-square fluctuations of the effective activation frequency and quantum oscillator frequency.
• The calculated mean-square fluctuations of the distribution function parameters indicate they do not influence a large entropy fluctuation to the same extent. Here the activation barrier is represented as a set of non-ideal quantum oscillators where the degeneracy and exclusion of some exited vibration levels are taken into account.