Underwater Communication Using Acoustic Parametric Arrays ^†

Abstract

This paper presents a study of different types of parametric signals with application to submarine acoustic telecommunications. In all of them, the carrier frequency is 200 kHz, which corresponds to that resonation of the transducer under study, while they differ by the different modulations they present. In this sense, we study modulations with sweeps (4 to 40 kHz), in which represent binary codes (zeros and ones), getting closer to the application in acoustic telecommunications. The different properties of the transmitting signals in terms of communication speed, directivity, efficiency and power needed are discussed as well.

1. Introduction

Communications in underwater environments have become a field of research of great interest in recent years. Therefore, the development of submarine sensors have experienced a significant increase in transmission technologies in underwater communication systems. The transmission of information in underwater media can be based on acoustic systems. However, propagation of the waves in the underwater acoustic channel has important limitations because of limited bandwidth, extended multipath, severe fading, and refractive properties of the medium. Thus, new methods of communication are proposed based on non-linear propagation effect that allows directive communication by using directional high frequency transducers to produce a low-frequency secondary beam in the medium used for the communication application. With this, several advantages are foreseen: to communicate just in the desired direction, so being more robust against unwanted dissemination of information, or avoiding reflections or multi-path effects that could worsen the quality of the communication.

1.1. Parametric Effect

When a given acoustic beam with given frequencies propagates in a non-linear medium, secondary frequencies are formed, such as the addition or difference of the primary frequencies. This phenomenon, known as the parametric effect, was first studied by Westervelt [1], and later developed and applied [2,3].

In general, if the emitted wave has a high carrier frequency (primary beam), it interferes and is rapidly absorbed in the medium allowing the low frequencies formed (secondary beam) to propagate at greater distances. As it is well known, it is easier to generate very directional high frequency beams than lower ones, which are usually more omni directional like. However, one of the fundamental characteristics of the parametric effect is that low frequencies, when generated, have a rather narrow directivity, comparable to that of the primary beam [3].

Theoretical studies have determined that the shape of the secondary beam signal is the second derivative of the square envelope of the emitted signal, its amplitude being proportional to the square of that of the primary beam. The waveform of the secondary beam is determined by the following equation:

$$p \left(x,t\right)=\left(1+\frac{B}{2A}\right)\frac{p^{2}S}{16\pi \rho c^4\alpha x} \frac{{\delta }^2}{\delta t^2} {\left[f\left(t-\frac{x}{c}\right)\right]}^2 ~ \frac{{\delta }^2}{\delta t^2} f^2$$

(1)

where S is the area of the vibrating surface of the transducer, f(t − x/c)² is the envelope of modulation, x is the distance to the source and t is time, B/A is the nonlinearity parameter of the medium, ρ density, c the velocity of sound and α the absorption coefficient in the medium. Therefore, the resulting wave p(x, t) will be proportional to the second derivative of the square envelope of the emitted signal [4,5,6].

1.2. Approach

Firstly, this paper proposes a theoretical study with different equations in order to optimize the acoustic parameters of an underwater communication system in order to be able to evaluate its performance in function of the signal-to-noise ratio and the maximum level of the source acoustic from the diameter of the transducer [7].

Secondly, a study of measured signals is carried out by a plane emitter transducer, characterizing it through the magnitudes of directivity and voltage variation. In order to do this, an analysis of the measurements are performed by correlating the emitted signal with the received one and thus obtaining the primary beam, and subsequently the second derivative of the envelope to the square of the signal sent with the received signal filtered at low frequencies, to obtain the secondary beam or parametric signal in question.

2. Hardware Consideration

The formulations are presented below for the level of the secundary beam signal Bertay and Leahy [3]. This model takes into account that the shock wave may be a potential problem to control secondary beam modulation, is based on a design for AUV’s communication systems, the equations allow simple calculations that can be used for circular piston arrays, and other such as square or rectangular shapes [8].

As input parameters are: fp carrier frequency in kHz, fs secondary beam frequency in kHz, d diameter in m and thus obtain; SLs (dB/uPa@1 m) secondary beam pressure level, NL (dB/uPa) noise, transducer power Wo, TL (20 km) transmission noise, DI (dB) directivity, SNR (1kHz) signal-to-noise-ratio, SLp primary beam pressure level, SLc critical source level at the center primary frecuency at which saturation.

The following equations are presented for the design:

$$S=\left(\frac{\pi d^2}{4}\right) \mathrm{Radiating}\mathrm{Surface}$$

(2)

$$Wo=\left(4\pi · {10}^6· {1.7}^2\right)/f_p$$

(3)

$$SLp=10logWo+171+10\log \left(4\pi S/{\lambda }^2\right)$$

(4)

$$SLs=2SLp+20\log \left(fs\right)kHz+20og(\Delta )-287$$

(5)

$$\Delta ={{\displaystyle \int }}_0^{\infty }\frac{e^{-x}}{x+Z} d,Z={\alpha }_T{R}_{p }\left(f_p/f_s\right),R_p=\left(S/{\lambda }_p\right),$$

$${\alpha }_T=2{\alpha }_p-{\alpha }_s(\mathrm{Np}/\mathrm{m})\mathrm{Effective}\mathrm{length}\mathrm{of}\mathrm{the}\mathrm{parametric}\mathrm{array}$$

(6)

$$S{L}_c=20logL-20\log \left(f_p\right)\mathrm{kHz}+292$$

(7)

$$TL=60+20log{R}_{km}+{\alpha }_{s}R$$

(8)

$$NL=60-17log{f}_s,DI=10 (4\pi S/{\lambda }_s^2)$$

(9)

$$SNR=S{L}_s-TL-NL+DI-10log B$$

(10)

2.1. Transmitter Acoustic Response

As an example, these equations are applied to the emitter transducer studied in this paper Airmar P19 with a ceramic diameter of 0.033 m, the results are presented for a 1 kHz bandwidth in the next

Table 1. Results for a 1 kHz bandwidth on 20 km.

fs (kHz)	Potencia (W)	TL (20 km)	NL (dB/uPa@1 m)	DI (dB)	SLp (dB)	SLc (dB)	SLs (dB)	SNR (1 kHz)
40	182	111	33	9	216	225	179	60

.

It was observed in the table that for our transducer, the value for SNR is very high, this is because it is difficult assumptions on noise level (may be considerably higher) on transmission loss [8]. Even so, with this example we can show the potential of the parametric array concept serving as the basis for the design not of a transducer but of an array in question.

3. Experimental Setup

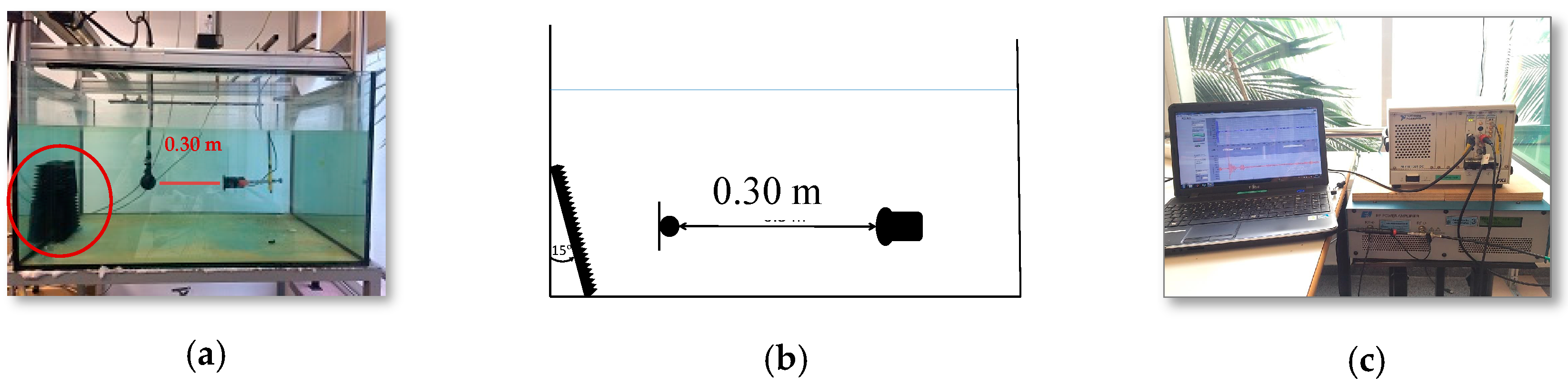
All measurements have been made in a water tank of size 1.12 × 0.96 × 0.51 m³. Figure 1a,b shows the experimental setup where the distance between the emitter and the receiver is 0.30 m with an absorbent inclined ~10° panel located on the rear wall of the ITC 1032 receiver transducer in order to avoid certain reflections. This transducer has a reception sensitivity (RVR) of −194 dB re 1 V/µPa and a resonance frequency at 33 kHz, sensitive to the low frequencies to be detected. The transmitter is the Airmar P19 plane transducer. A sampling frequency fs = 20 MHz is used. Figure 1b shows the measurement instruments where the transmitter transducer is connected through the National Instruments 5412 PXI by amplifying the signal with the E&I 2100L RF amplifier. Signal reception is done through the PXI National Instruments 5102 card.

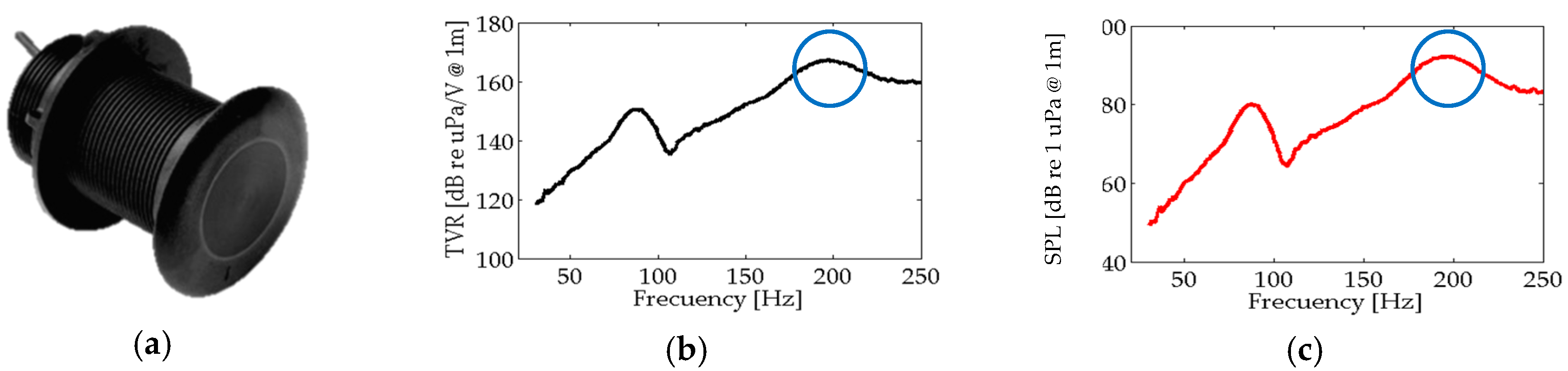
3.1. Technical specification for Airmar P19 plane transducer

The Figure 2b, shows the Transmiting Voltaje Response (TVR) of Airmar P19 in 167 dB re µPa/V@1 m for the resonance frequency at 200 kHz to be used as the modulated carrier frequency (fp). In Figure 2c, the sound pressure level is presented, with a value for the frequency of 200 kHz of 195 dB re uPa@1 m.

4. Results

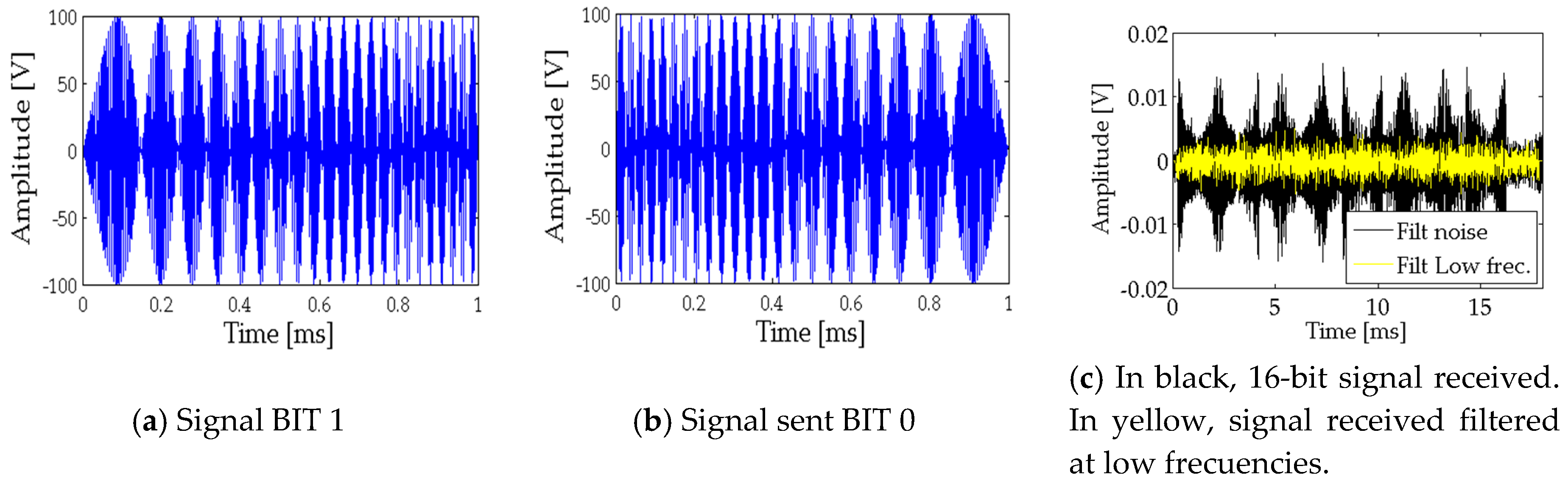
A parametric sweep with a frequency bandwidth of 4 to 40 kHz with a duration of 1 ms and a carrier frequency fp = 200 kHz is presented. The intention is to generate a 16 bit = 1010010110010110, string of ones and zeros with this signal; where bit 1 corresponds to the sweep of 4 to 40 kHz and bit 0 corresponds to a sweep of 40 to 4 kHz and through cross-correlation to detect these bits on time. All of this, in order to be able to send messages in acoustic communications at low frequencies with high directivity.

The signals sent for bit 1 and bits 0, and the resulting signal received for each of them, are shown below.

In Figure 3c, the received signal is filtered at low frequencies, whit a low pass filter of 2 to 60 kHz being applied so as to be able to correlate such signal with the second derivative of the envelope to the square of the signal sent to obtain the secondary beam.

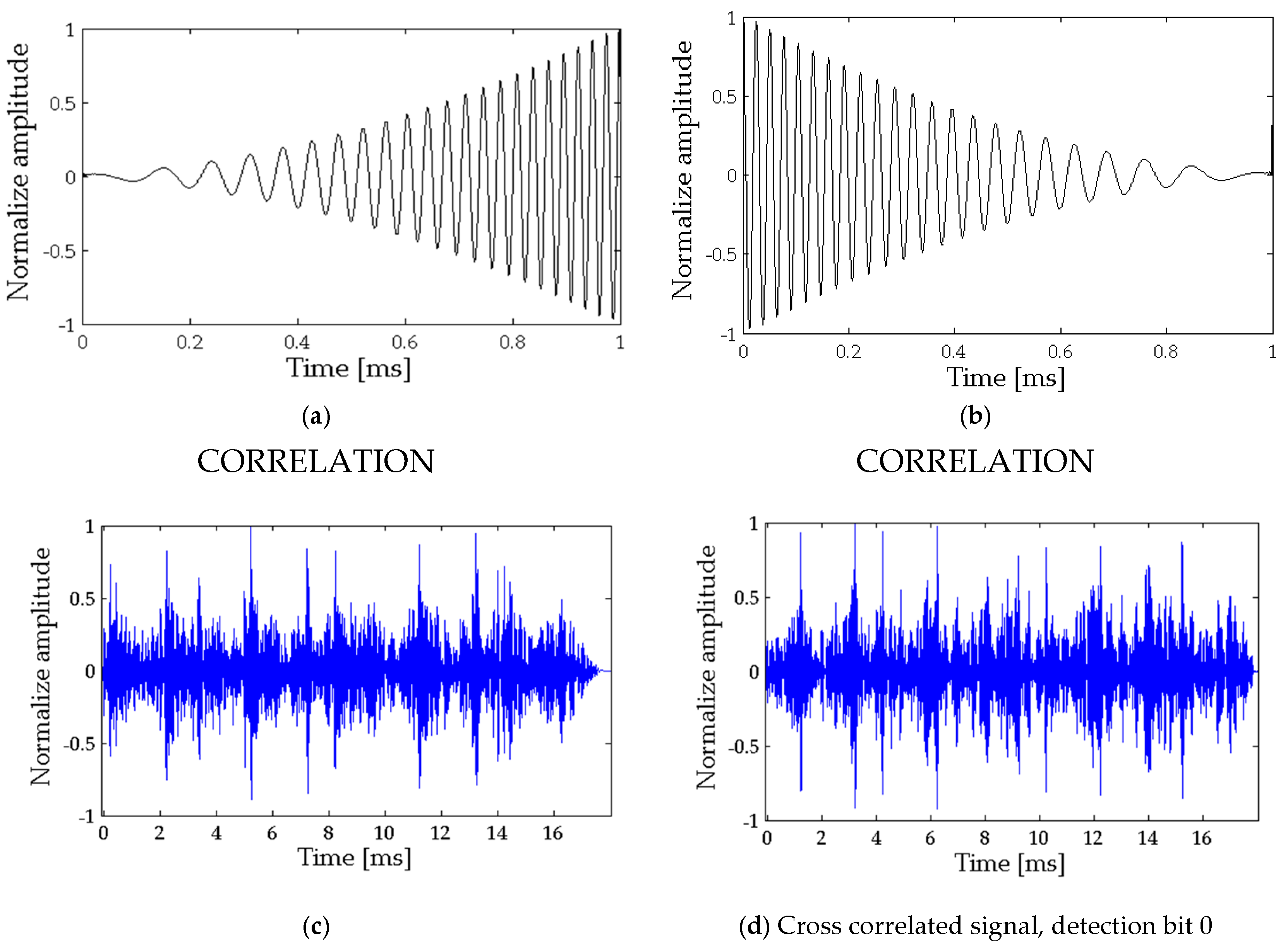
Next, the correlation of the received signal with the second derivative of the envelope to the square of the sent signal (the secondary beam) for each bit is shown, as seen in Figure 4a,b, respectively.

Figure 4c,d show the detections for bits 1 and 0. In Table 2 the detection times for a direct flight time of 0.2 ms, the relative amplitudes obtained after the cross-correlation and the assigned bit is presented, showing that the information could easily be extracted.

Finally, the directivity for the signal generated together with the voltage variation is presented.

In Figure 5a, it can be observed that the directivity pattern for both signals clearly shows the evidence of the parametric effect of the secondary beam, presenting a directivity similar to that of the primary beam with an opening angle of 15° and 9° respectively. In Figure 5b, a non-linearity for the secondary beam is presented as the voltage is increased. Both effects agree that the signal has been generated parametrically and thus, this technique could be used for acoustic underwater communications in circumstances that highly directive beams are preferable.

Figure 4. Signal analysis for detection of bit 1 and 0 by correlation. (a) 2nd time derivative of envelope—upward sweep; (b) 2nd time derivative of envelope—down sweep; (c) Correlated signal, detection bit 1; (d) Correlated signal, detection bit 1.

Figure 4. Signal analysis for detection of bit 1 and 0 by correlation. (a) 2nd time derivative of envelope—upward sweep; (b) 2nd time derivative of envelope—down sweep; (c) Correlated signal, detection bit 1; (d) Correlated signal, detection bit 1.

Table 2. Parameters of the detection and interpretation of the 16-bit signal received.

Detection Time (ms)	Amplitude bit 1	Amplitude bit 0	n
0.22	0.69	0.12	1
1.22	0.17	0.93	0
2.22	0.82	0.15	1
3.22	0.17	1	0
4.22	0.25	0.94	0
5.22	1	0.16	1
6.21	0.25	0.97	0
7.21	0.83	0.20	1
8.22	0.82	0.18	1
9.22	0.37	0.77	0
10.22	0.22	0.83	0
11.22	0.84	0.23	1
12.22	0.23	0.83	0
13.22	0.95	0.18	1
14.22	0.72	0.24	1
15.22	0.17	0.88	0
Mean	0.83	0.89

Table 2. Parameters of the detection and interpretation of the 16-bit signal received.

Detection Time (ms)	Amplitude bit 1	Amplitude bit 0	n
0.22	0.69	0.12	1
1.22	0.17	0.93	0
2.22	0.82	0.15	1
3.22	0.17	1	0
4.22	0.25	0.94	0
5.22	1	0.16	1
6.21	0.25	0.97	0
7.21	0.83	0.20	1
8.22	0.82	0.18	1
9.22	0.37	0.77	0
10.22	0.22	0.83	0
11.22	0.84	0.23	1
12.22	0.23	0.83	0
13.22	0.95	0.18	1
14.22	0.72	0.24	1
15.22	0.17	0.88	0
Mean	0.83	0.89

Figure 5. Magnitudes to characterize. (a) Directivity; (b) Tension variation.

Figure 5. Magnitudes to characterize. (a) Directivity; (b) Tension variation.

5. Conclusions

The formulations presented to optimize the design of an array according to the model of Bertay and Leahy, lay the foundations for developing the design of a parametric array.

The generation and analysis of parametric signals for a plane emitter transducer has been discussed in order to apply it to underwater acoustic communications. With respect to this, we can conclude that the parametric generation allows a better use of the communication channel which allows to transmit in a more defined region, in addition to improving the resistance against possible background noise and interference.

On the other hand, the rapid absorption of high frequencies in the medium allows the low frequencies (secondary beam) to propagate at greater distances with a rather narrow directivity angle of the order of 15° for a frequency bandwidth between the 4 and 40 kHz presented in this study, comparing it with conventional transducers with a directivity angle of ~60°.