Theoretical Study of Quasi-Longitudinal Lamb Modes in SiN/c-AlN Thin Composite Plates for Liquid Sensing Applications ^†

Abstract

The propagation of quasi-longitudinal Lamb mode along SiN/c-AlN thin composite plates was modeled and analyzed aimed at the design of a sensor able to detect the parameters change of a liquid environment, such as added mass and viscosity changes. Three modes were identified that have high phase velocity and quite good electroacoustic coupling efficiency: the fundamental quasi symmetric mode (qS₀) and two higher order quasi-longitudinal modes (qL₁ and qL₂) with a dominantly longitudinal displacement component at one plate side. The velocity and attenuation of these modes were calculated for different liquid viscosities, and the gravimetric and viscosity sensitivities of both the phase velocity and attenuation were theoretically calculated.

1. Introduction

The propagation of in-plane polarized Lamb modes along thin piezoelectric plates has been previously reported [1], aiming at the design of electroacoustic devices able to work in liquids. Higher order quasi-longitudinally polarized Lamb modes exist that travel at velocities close to that of the longitudinal bulk acoustic wave propagating in the same direction. They have close-to-zero shear vertical particle displacement component at the surface of the plate contacting the liquid environment, that can prevent acoustic energy leakage into the liquid. Moreover, their high velocity makes them suitable for high operating frequencies. Matlab, Disperse, and COMSOL Multiphysics simulations were used to study the dispersion curves and the acoustic field profile of the fundamental and higher order modes traveling in SiN/AlN thin suspended membranes, for fixed SiN and AlN thicknesses (200 nm and 1.4 μm) and variable wavelength λ. Two higher order modes, qS₁ and qS₂, were found that are slowly dispersive and have dominant longitudinal particle displacement component, at AlN thickness-to-wavelength ratio h_AlN/λ = 0.8 and 1.6 respectively. The acoustic field profile of the modes shows that the out-of-plane particle displacement are close to zero at one plate side. The electroacoustic coupling coefficient K² dispersion curves were studied for four different electroacoustic coupling configurations, based on interdigital transducers (IDTs) positioned at one of the AlN surface, with or without a metal floating electrode at the opposite layer surface. The theoretical gravimetric sensitivity in air and the sensitivity to the density-viscosity product of a Newtonian liquid contacting the device was calculated for the three modes.

2. Phase Velocity Dispersion Curves

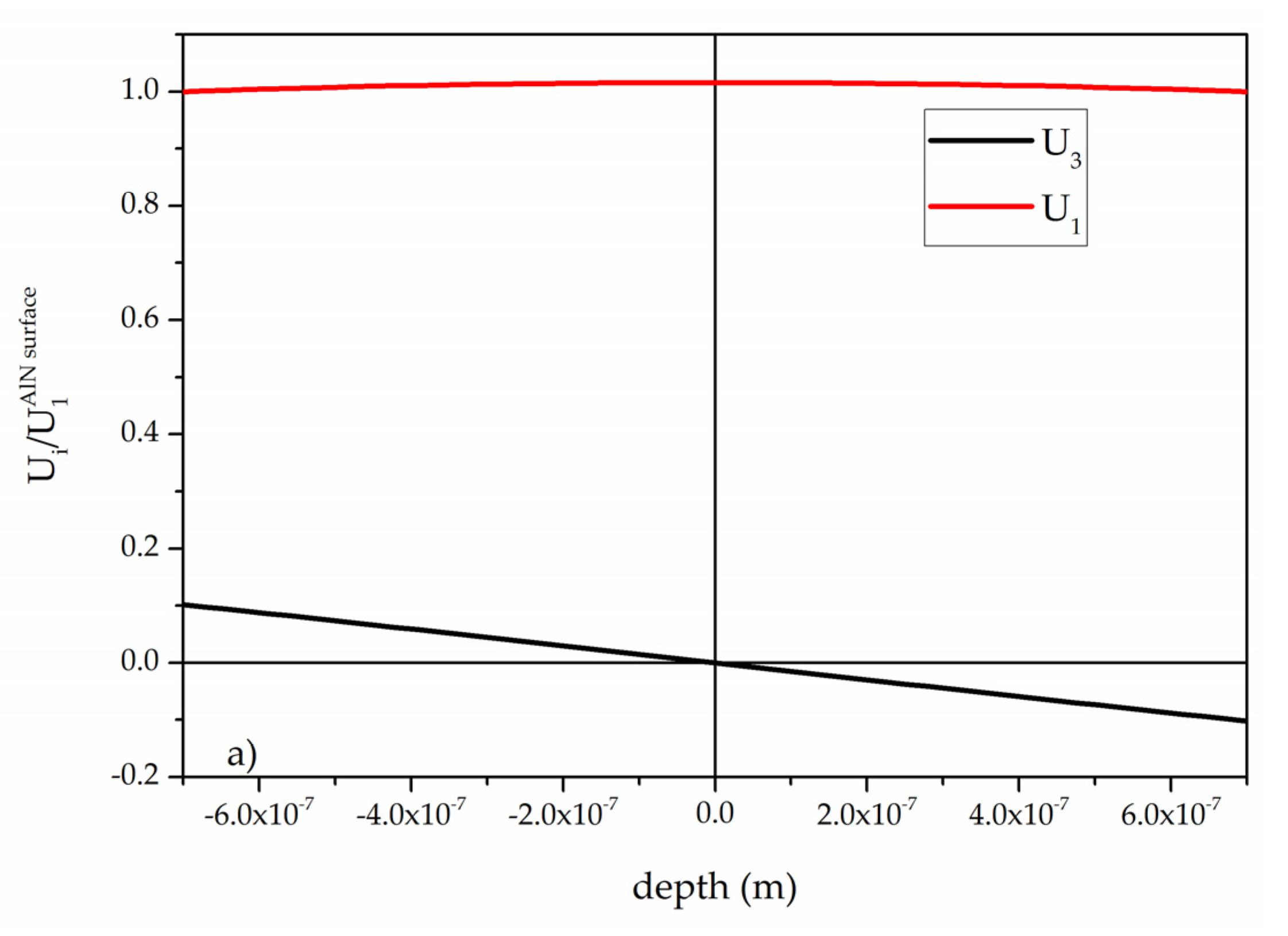
Lamb waves are acoustic modes that travel along finite thickness plates. The modes are divided into symmetric and anti-symmetric modes, S_n and A_n, (n is the mode order) with respect to the mid-plane of the plate. A single material thin plate, even anisotropic, shows a family of modes dispersion curves with evident flat regions belonging to the symmetric mode type: as an example Figure 1 shows the velocity vs. frequency dispersion curves for a c-AlN plate with thickness H equal to 1.4 μm.

Some symmetric modes can be identified that are suitable for liquid sensing applications as the shear vertical U₃ displacement component is close to zero at both sides of the symmetric plate. Figure 2a–d show, as an example, the field profile of the first four quasi symmetric modes, qS₀, qS₁, qS₂ and qS₃: these modes are symmetric as the longitudinal component U₁ is symmetric with respect to the mid-plane of the plate, while U₃ is antisymmetric. The two particle displacement components U₁ and U₃ are normalized at the U₁ value at the free AlN side; the shear horizontal displacement component U₂ is zero.

The four modes frequencies are: 285.54, 5623.85, 11145.2 and 16612.7 MHz, respectively. They travel at velocity equal to 10,868.1, 11,343.9, 11,351.9, and 11,357.5 m/s, respectively. Generally, one way to obtain a thin AlN suspended membrane consist in the AlN layer deposition onto a silicon wafer covered with a thin SiN or SiO₂ layer; the latter film acts as a stop etching layer during the silicon micromachining process. Thus the final suspended membrane is a bilayered membrane (SiN/AlN) that has no symmetry with respect to the mid-plane of the plate: the Lamb modes dispersion curves for this composite plate are expected to be different from those shown in Figure 1 and referred to a single material plate (AlN) [2]. The flat regions are shorter than the previous case and the modes cannot be anymore identified as symmetric or antisymmetric: the modes will be named hereafter with an increasing number. 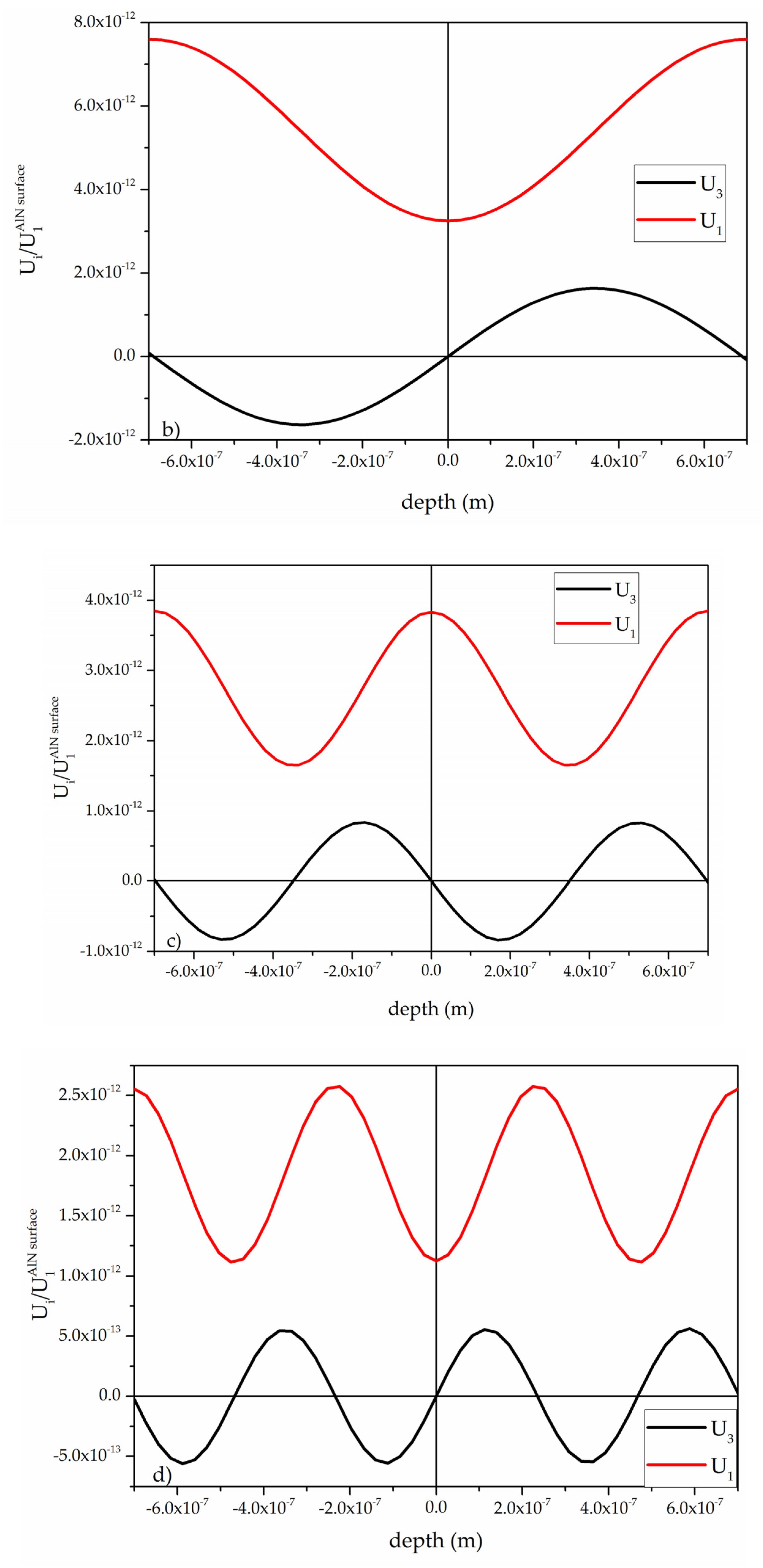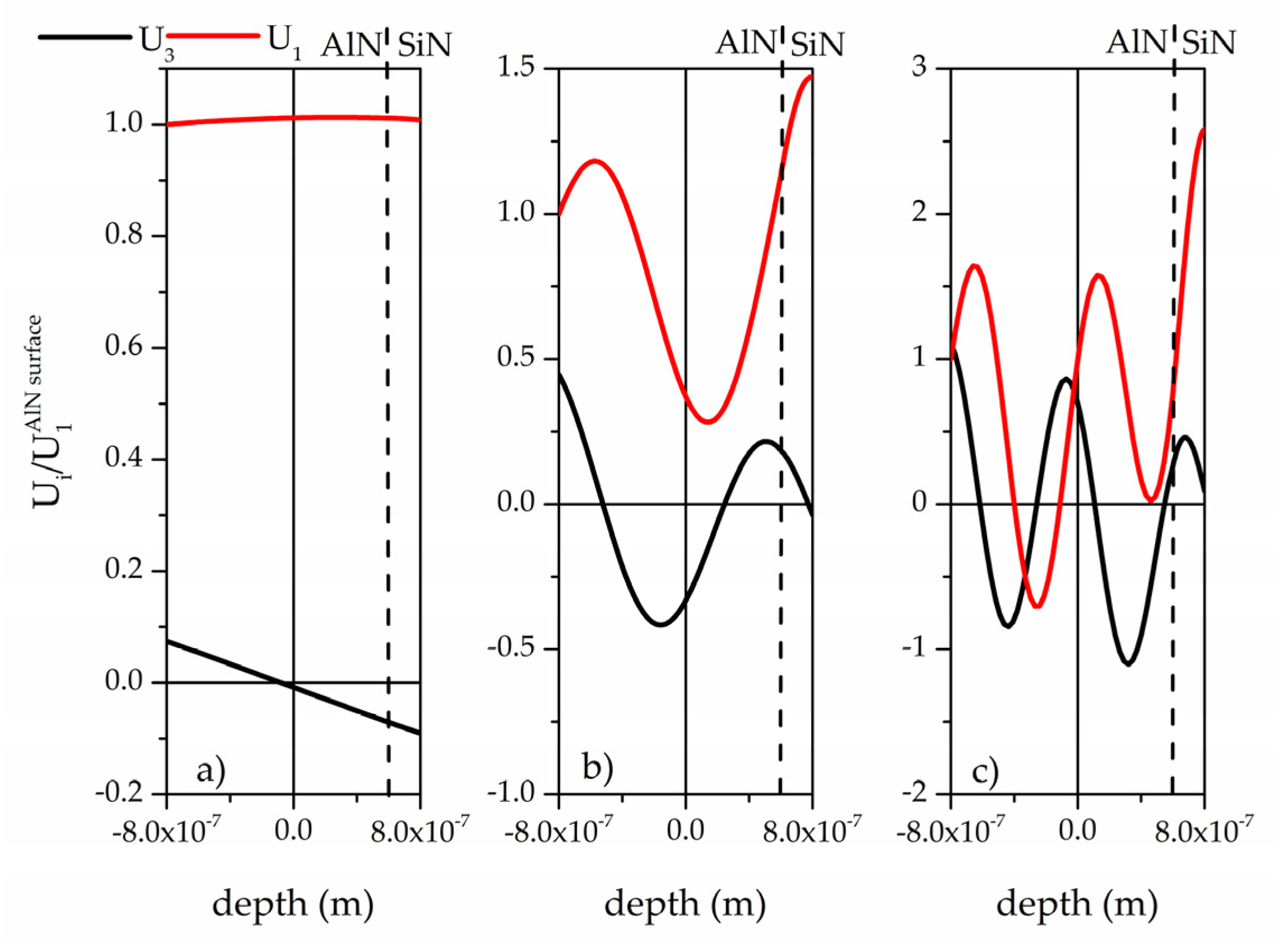As an example, Figure 3 shows the dispersion curves of the Lamb modes travelling along the composite plate AlN/SiN with total thickness H_total = 1.6 μm, being 1.4 μm and 0.2 μm the AlN and SiN thicknesses.

Three modes were identified that travel along the SiN/AlN composite plate and that are suitable for liquid sensing applications. Figure 4a–c shows the field profile of these three quasi symmetric modes, qS₀, qL₁, and qL₂: the corresponding H_total/ λ values are 0.08, 0.80 and 1.6. As it can be seen, U₃ is very low with respect to U₁ (U₃ << U₁) on one plate side that is thus the one suitable for contacting a liquid environment.

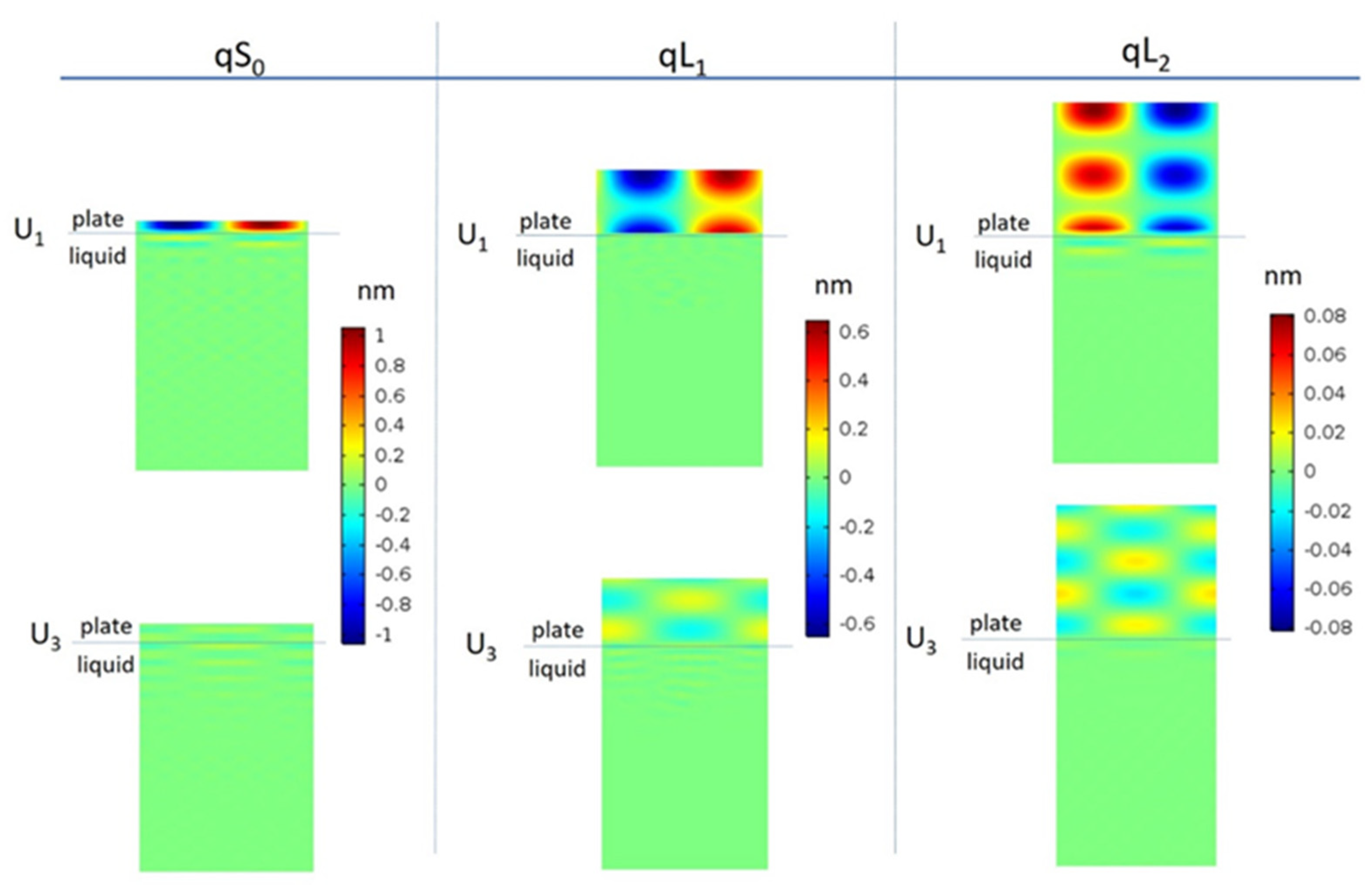
COMSOL FEM Multiphysics software was employed to simulate the three modes propagation along the composite plate with the liquid (water) contacting the plate surface. 2D piezoelectric device simulation with solid mechanics and electrostatic modules was used for eigen-frequency analysis of the composite plate. The number of degrees of freedom to solve for the mode is minimized by providing periodic boundary conditions to the transmitting IDTs which is a one-finger structure with a total width of one λ. Figure 5 shows the field profile of the three modes in the SiN/AlN plate contacting the liquid environment (water) from the SiN side of the plate. As can be seen, the acoustic energy is confined inside the plate.

3. The Coupling Efficiency

The electroacoustic coupling coefficient, K², physically represents the IDT electrical to acoustic energy conversion efficiency: it is frequency dispersive and strongly affected by the electrical boundary conditions. In the SiN/AlN plate, four piezoelectric coupling configurations can be obtained by placing the IDT at the SiN/AlN interface (SiN-Transducer- Film, STF) or at the AlN surface (SiN- Film-Transducer, SFT), further including a floating metal electrode onto the AlN layer side opposite to that where the IDT is located (SiN-Transducer-Film-Metal and SiN-Metal- Film-Transducer, STFM and SMFT). The four configurations are depicted in Figure 6.

FEM analysis was performed using COMSOL 5.2 to calculate the K² as K² ≈ 2[(v_f − v_m)/v_f], where v_f and v_m are the velocities along the electrically open and shorted surfaces of the AlN film. In

Table 1. The K² of the four coupling configurations for each mode in the SiN (200 nm)/AlN (1.4 µm) plate, for λ = 20, 2, and 1 µm.

Mode/K2 (%)	Coupling Configuration
	SFT	SMFT	STF	STFM
qS0	0.22%	2.98%	0.14%	2.90%
qL1	0.91%	0.90%	0.039	0.026%
qL2	0.55%	0.55%	0.01%	0.011%

the K² of the four coupling configurations are summarized for each mode.

4. Lamb Wave Sensor

4.1. Mass Sensor

A mass accumulation on the device surface changes the surface density of the propagating medium, hence resulting in a mode velocity shift. The gravimetric sensitivity S_m in air of the three modes on each side of the composite plate was calculated as the relative velocity shift per unit added mass, ${\mathrm{S}}_{\mathrm{m}}=\left(\raisebox{1ex}{${\mathrm{v}}_{\mathrm{b}}-{\mathrm{v}}_{\mathrm{l}}$}\!\left/ \!\raisebox{-1ex}{${\mathrm{v}}_{\mathrm{b}}$}\right.\right)/{\mathrm{m}}_{\mathrm{am}}$, being v_b and v_l the velocity of the bare and loaded plate, m_am = ρ·d, ρ and d the added mass density and thickness. The S_m at the AlN side was equal to -630, -2400 and −2383 cm² g⁻¹, while at the SiN side was equal to −640, −3770 and −2425 cm² g⁻¹, for the qS₀, qL₁ and qL₂ modes, respectively. The gravimetric detection occurring at the AlN or SiN sensing surface of the same plate shows different efficiency as a consequence of a different mode energy confinement at the plate’s sides: the highest gravimetric sensitivity is achieved for the plate sensing surface that transmits an higher amount of acoustic energy to the mass loading layer.

4.2. Viscosity Sensor

When a liquid contacts the acoustic waveguide, the in-plane particle displacement component of the acoustic mode couples to a very thin viscous boundary layer of thickness δ = (2η/ωρ_l)^0.5, where η and ρ_l are the liquid viscosity and mass density. The viscous liquid was supposed to be a mixture of water and glycerol; the fraction of glycerol by volume ranged from 0 (only water) to 0.53, and the $\sqrt{{\mathsf{\rho }\mathsf{\eta }}_{\mathrm{l}}}$ ranged from 0.95 to about 11 kg·m⁻²·s^−0.5. The real and imaginary parts of the phase velocity of the three modes were calculated for different concentrations of the water/glycerol mixtures. 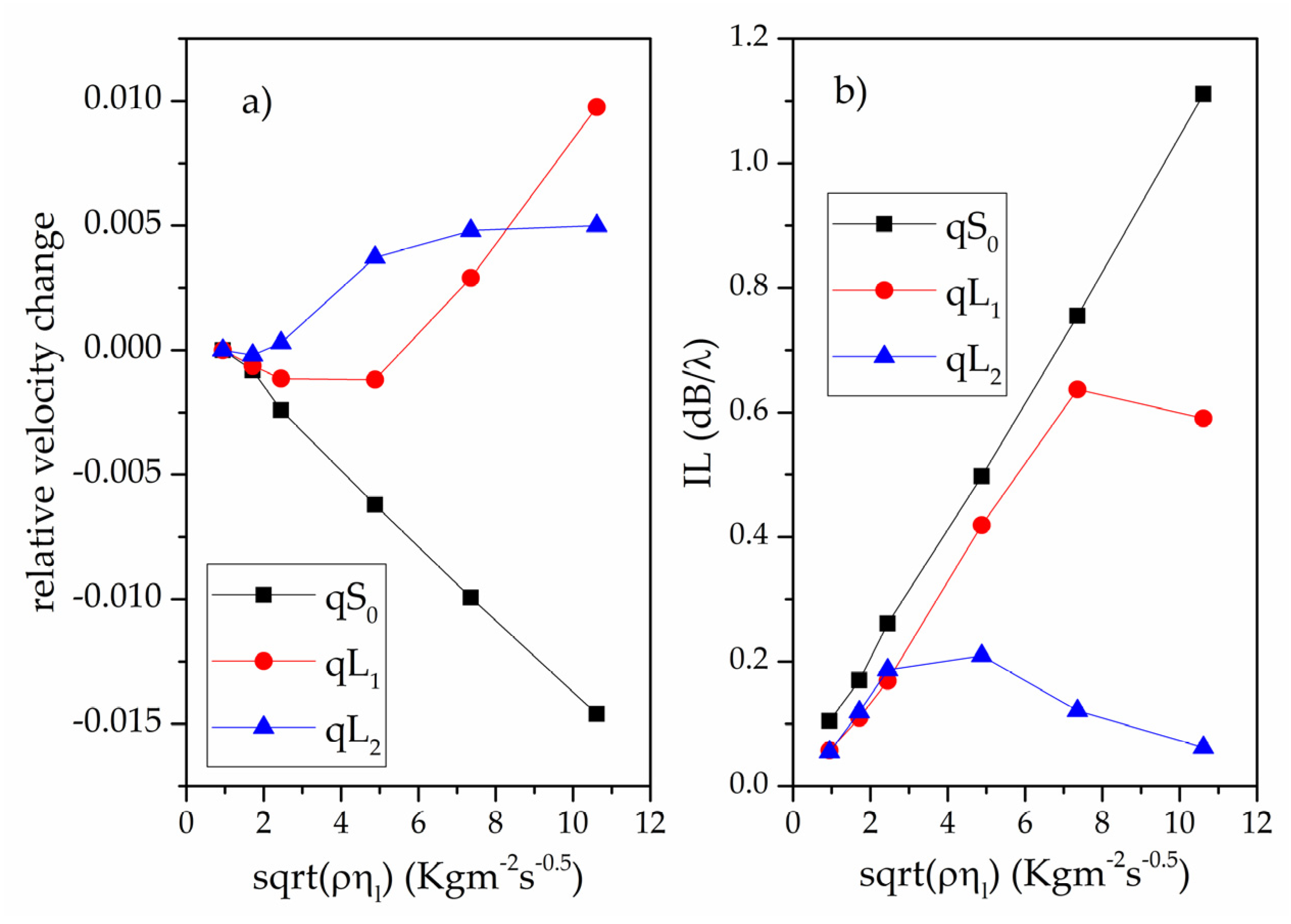The relative changes of the phase velocity Δv/v₀ and the IL as a function of $\sqrt{{\mathsf{\rho }\mathsf{\eta }}_{\mathrm{l}}}$ are shown in Figure 7a,b where it is assumed that the examined glycerol-water mixture contacts the SiN surface of the composite plate.

The qS₀ mode has a linear IL and relative velocity shift behavior vs. the $\sqrt{{\mathsf{\rho }\mathsf{\eta }}_{\mathrm{l}}}$ values in the studied viscosity range: its time period (2.06 ns) is far larger than the fluid relaxation time τ = η/μ (where μ is the liquid shear modulus) for the 0.9 to 11 abscissa value. The qS₀ velocity and attenuation sensitivities are −0.0015 m² s^0.5 kg⁻¹ and 0.1038 dB/λ m² s^0.5 kg⁻¹. The relative velocity shift of the qL₁ mode is linearly dependent on $\sqrt{{\mathsf{\rho }\mathsf{\eta }}_{\mathrm{l}}}$ only for low viscosity values, and its slope is reversed for glycerol/water percentage ≥ 20%, as τ becomes close to the wave period (0.2 ns) of the mode. The relative velocity shift of the qL₂ mode is linearly dependent on $\sqrt{{\mathsf{\rho }\mathsf{\eta }}_{\mathrm{l}}}$ for very low viscosity values, and is reversed for glycerol/water percentage ≥ 10%, as τ becomes close to the wave period (0.099 ns) of the mode.

5. Works in Progress

Cr/Au IDTs were implemented onto the bare SiN thin suspended membrane (200 nm thick, and with the area equal to 1.5 mm × 1.5 mm) by electron beam lithography (EBL): the IDTs width of 0.5 μm (equal to λ/4) was achieved with EBL onto the SiN suspended membrane (λ = 2 μm). A c-AlN layer was deposited by rf magnetron sputtering technique onto a reduced area of the surface of the SiN membrane by using a shadow mask with an opening area of 1 mm × 1 mm, thus an AlN layer was sputtered having an “island-like” structure, as shown in Figure 8.

The use of a mask is a method that offers the remarkable advantage to reduce the complexity of the device fabrication process based on several technological steps, including the silicon substrate surface or bulk micromachining and the etching of a sacrificial layer to release the membrane.

6. Conclusions

The propagation of quasi Lamb modes along SiN/AlN composite plates have been theoretically investigated. The displacement profiles, phase velocities, and the electromechanical coupling coefficients of four coupling configurations have been calculated, specifically addressing the design of enhanced-coupling, microwave frequency sensors for liquid environments. The IL and velocity changes of the qS₀, qL₁, and qL₂ modes when contacting a viscous Newtonian liquid have been calculated for different viscosities. The SiN/AlN-based sensors are proven to achieve remarkable performances (high sensitivity and enhanced coupling efficiency) that are important prerequisites for the design of future devices to be used in the context of chemical, biological, and physical quantities detection.