Effects of Some Geometric Parameters in Energy-Efficient Heat Distribution of Pre-Insulated Double Pipes ^†

Abstract

In the case of a computational example, a few aspects of the twin pipe geometry are presented, which have an effect on heat losses through double heating ducts. Proper positioning of the supply and return ducts in common thermal insulation can significantly improve the efficiency of the heating network and reduce heat losses. In this work, unit heat losses generated by the example double heating ducts and unit heat flux of the supply, return and exchange between the supply and return pipes as a function of the distance between the supply and return pipes were determined. On the basis of graphs of unit heat fluxes as a function of the distance between the duct and the return, one can formulate the optimal solution of the position, the supply and return duct in common insulation. In an optimal solution for the location of the supply and return ducts in a common insulation, both the total heat losses and the heat flux exchanged between the supply and return ducts should be minimal. All calculations were made in a proprietary calculation program written in Fortran language within the framework of the VIPSKILLS project. The work also presents solutions of temperature fields and heatlines in the cross-section of the duct of a dual heating network in the presented example.

1. Introduction

The basis for rational energy management is not only the selection and proper use of a heat source, but also the distribution of heat. The distribution of heat is associated with the appropriate selection of pipes and service pipes. Currently, twin pipes (double heating ducts) are becoming more popular, which are implemented with a common insulation. Twin pipes can be used as underground networks and as aboveground heating networks (Figure 1). The main advantage of a double pipe system compared to a single system is the lower construction cost. The location of double heating pipes in a common insulation slightly complicates the heat flow in double pipes compared to single pipes, in which analytical solutions can be used to determine heat losses. Heat losses in double pipes depend not only on the temperature of the medium, the thickness of thermal insulation and thermal insulation coefficient of thermal insulation, but also depend on the geometry of the location of the pipes inside the insulation.

Heating networks are the subject of many studies. Persson and Claesson [1] presented formulas for calculation of steady-state heat losses from annularly insulated pipes using the multipole method. Bøhm and Kristjansson [2] compared heat losses in single, twin and triple (two supply pipes and one return pipe) buried heating pipes. Figure 2 shows an example of the arrangement of the supply and return pipes in the cross-section of the duct of a dual heating network. Determining heat flows in pre-insulated double ducts can be helpful in reducing heat losses and heating network optimization through appropriate location of a double duct in a common thermal insulation. The purpose of this publication is the numerical analysis of heat exchange for different locations of double pipes in the thermal insulation layer. The calculations were made using the boundary element method, which was used in the calculation program as part of the VIPSKILLS project [3].

2. Calculation Example of a Twin Pipe

In order to determine the heat losses, two pipes of the same diameter d = 90 mm in round insulation with a diameter of D = 250 mm made of polyurethane foam with a thermal conductivity coefficient of k = 0.0265 W/(mK) were assumed. On the outer surface of the insulation, a constant ground temperature was adopted, which was T₀ = 8 °C. The wall temperature of the supply pipe is equal to the temperature of the flowing liquid at T_S = 90 °C. The wall temperature of the return pipe has been set in the range of 50 °C < T_R < 80 °C. The calculations were made for the assumed distance s between the supply and return pipes in the range 0 < s < 70mm. In Poland design supply water temperature in a heating season is mostly set at 120 °C (return 55 °C), whereas after the heating season when a network supplies fluid only for domestic hot water proposes values are lower: 70 °C and 42 °C, respectively.

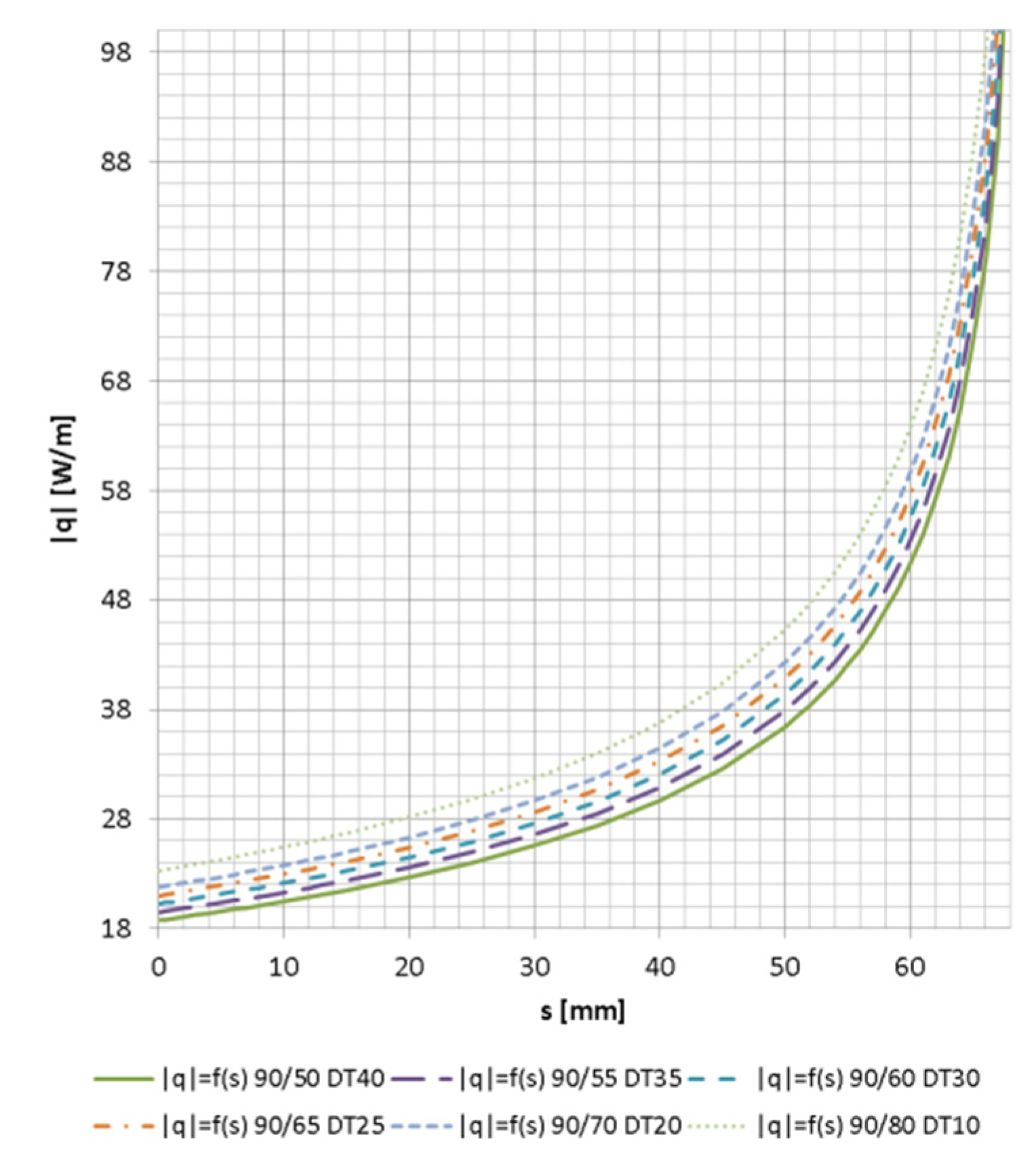
Figure 3 shows the unit heat losses through a double pre-insulated pipe for different distances s between the supply and return pipes and for different temperatures T_R. The smaller the difference between the supply and return temperature (∆T = T_S − T_R) at the same supply temperature T_S, the greater the heat losses through the insulation of the pre-insulated double duct. With the increase in the distance s between the supply and return pipes, heat losses increase, which is associated with a smaller insulation thickness on the right and left side of the cross-section of the pre-insulated pipe. For example, for ∆T = 10 °C, pipes at a distance of s = 57 mm generate up to twice the heat loss compared to the distance s = 28 mm.

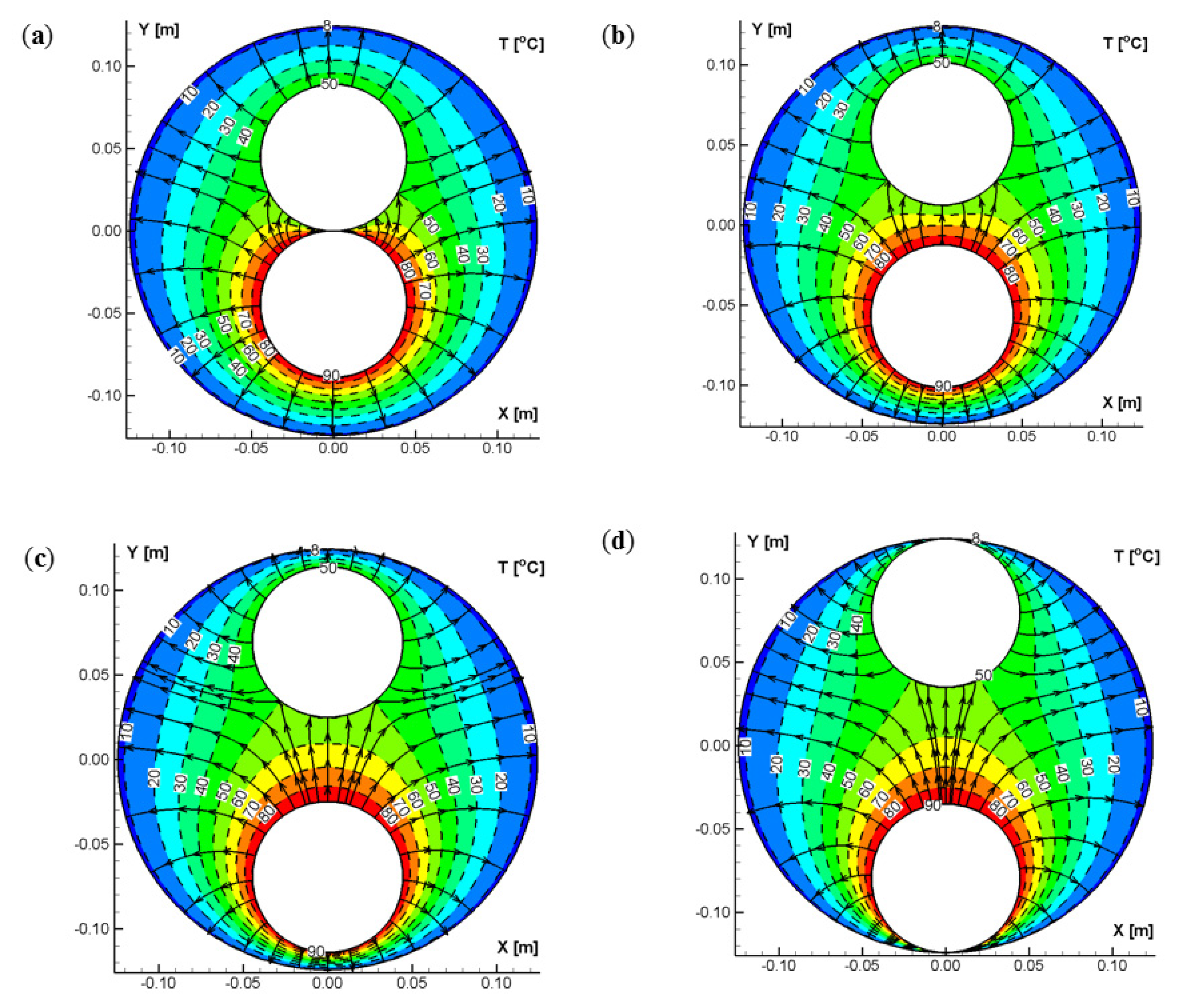
Figure 4a–d show examples of calculation results for temperature fields and heatlines for ∆T = 40 °C and for four selected distances s. Figure 4a–d indicate that with decreasing distance between the supply and return pipes, the field of q_R1 flux becomes larger.

3. Conclusions

The location of double pipes within the insulation significantly affects the heat loss in a heating network. Heat losses are particularly important in low-energy district heating systems.

If the supply pipe is too close to the return pipe, then heat flows from the supply pipe to the return pipe. If the supply and return pipes are too close to the outer insulation wall, both pipes generate significant heat losses. Based on the example shown, it can be concluded that the optimal spacing of the supply and return pipes is in a place where the heat losses for the supply and return pipes are minimal and the heat transfer between the supply and return pipes is also minimal. It should be noted here that in many thermal analyses of double pre-insulated networks, heat exchange between the supply and return pipes is ignored.